几何角度理解线性插值和双线性插值

已知两个点的坐标为\((x0,y0)\)和\((x1,y1)\)，他们呈简单的线性关系（或者近似）。带求坐标x落在\((x0,x1)\)之间，求y。

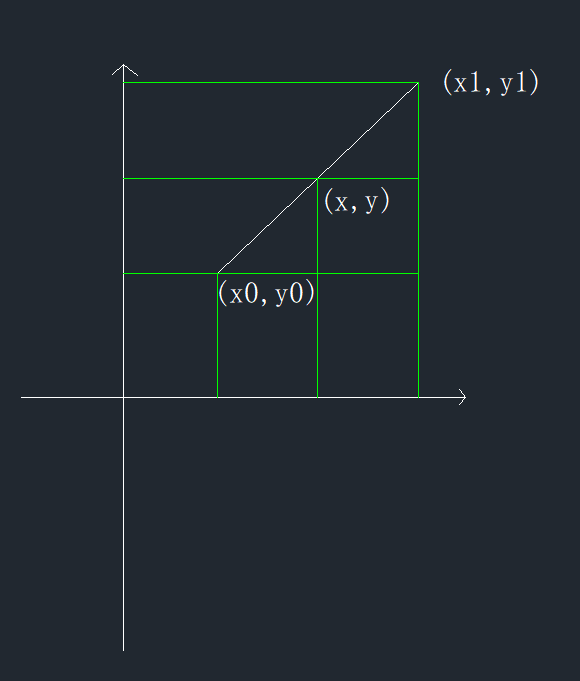
如上图白色的线。
从几何角度有两种方法，一是相似三角形，二是斜率相等。下面使用相似三角形可知：

\[{y-y0 \over x-x0} = {y1-y\over x1-x} \]

从而可得

\[y = {(x1-x)y0+(x-x0)y1\over x1-x0} \]

上面是线性插值的描述

已知图像上一点，其坐标是浮点数，求其灰度值。如下图：

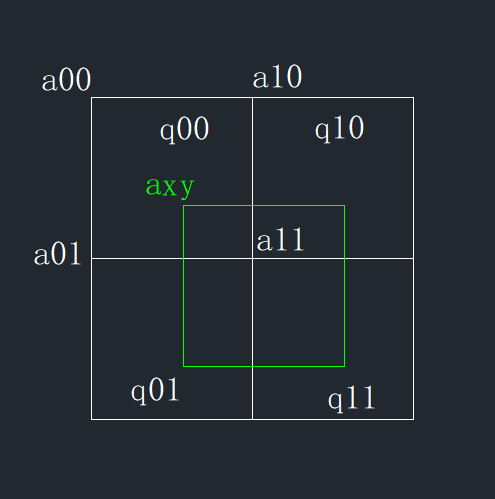
a00,a10,a01,a11是相邻的像素点，其灰度值都已知，求axy的灰度值。
从直观上看，axy的灰度值由另外四个像素的灰度值的一部分组成。若假设axy在另外四个像素中的面积的比重与灰度值所占比重呈线性关系，则很容易求出其灰度值来。

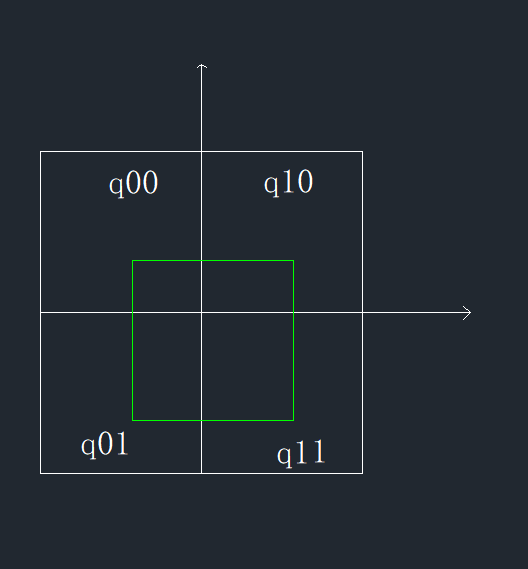
首先，将坐标原点平移到a11。并假设a11的坐标为\((x0,y0)\)。然后，将所有像素边长假设为1（归一化）。则可以求出来新像素的四个顶点。然后，依据其顶点坐标，求出面积。
因为像素边长已经归一化，故其面积为1。因此，求出的四个小方块的面积即表示其在该像素中所占的比重。

\[q = (x-x0)(y-y0)q00 + （x+1-x0)(y-y0)q10 + (x-x0)(y+1-y0)q01+(x+1-x0)(y+1-y0)q11 \]

上式的值，与一般的双线性插值算出来的值是一样的。