WerChange的OI博客

摘要： 提供一种思路，可以做到 \(O(n)\)。 update 2023.08.13 修改了 Latex 滥用问题。 update 2023.08.12 修改了空格问题。 update 2023.08.11 修改了空格问题。 update 2023.07.29 完工，期望无 bug （暑假快乐吖） upd 阅读全文

摘要： 07.12&07.14模拟赛总结 前言： 这是最戏剧性的一集，两场都是同级第一，只不过一场正数、一场倒数。 07.12——Day 1 T1 P8093 [USACO22JAN] Searching for Soulmates S 题目描述 Farmer John 的每头奶牛都想找到她们的灵魂伴侣—— 阅读全文

摘要： 07.06&07.11模拟赛总结 前言： 之前学了些新东西，所以只比了两场模拟赛，一场Atcoder，一场USACO。 改完题了，趁有空总结一下。 07.06——Day 1 T1 [ABC218D] Rectangles 题目描述 在一个\(2\)维的平面上有\(N\)个不同的点，编号为\(1,2, 阅读全文

摘要： 2023.7月初模拟赛总结 前言： 近期（约）3天比了3场模拟赛，都源于USACO。但是这3场我的成绩都很低，赛后一看题解被自己的智商哭死，实在看不下去了，决定要写一篇总结 Day 1 T1 P3132 [USACO16JAN] Angry Cows G 正解 DP，设\(f_i\)为使第\(i\) 阅读全文

摘要： 任意模数多项式乘法 前言： 在教练讲的时候脑子并不清醒，所以没听懂。后来自己看博客学会了，但目前只学了一种方法：可拆系数FFT。为了方便日后复习，决定先写下这个的笔记，关于三模数NTT下次再补。 建议：准备好演算纸和笔，本篇含有大量推算部分。 注：本篇文章是本蒟写的，dalao随便看看就好，不必争论 阅读全文

摘要： 二分图最大匹配 前言：其实老早就学了，但是之前学的时候不透彻，稀里糊涂背背模板就过去了。果然，在最近一次原题检测上找到了我，然后就“暴毙”了。 我就意识到学算法不能这么学，要摸清楚规律、掌握证明方法、思考推论过程。 俗话说“温故而知新”，的确，我也在复习的过程中有了更透彻的理解。所以我决定写一篇笔记 阅读全文

摘要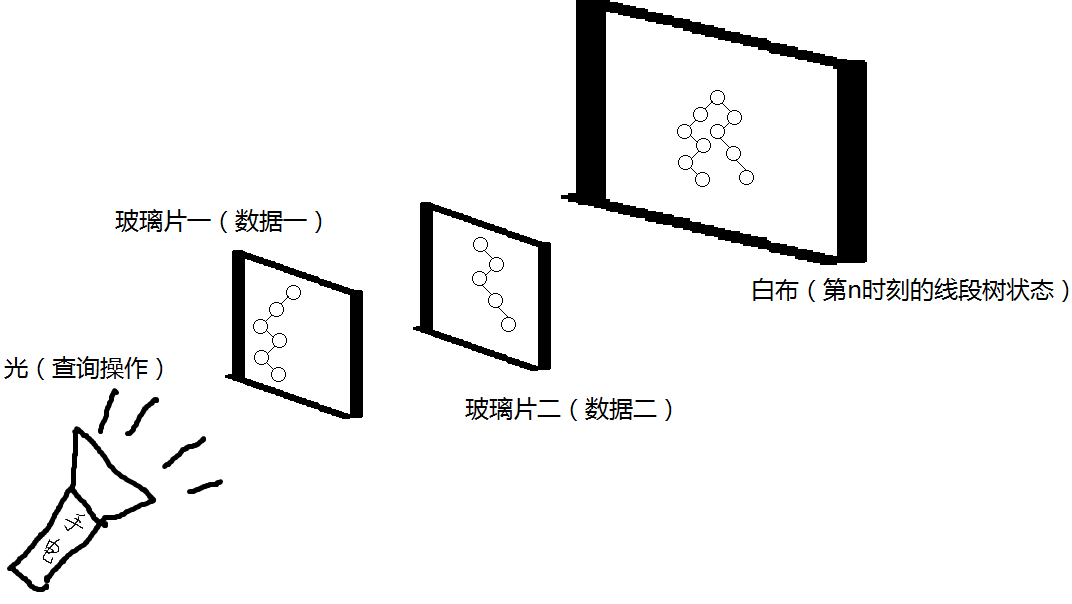： 可持续化线段树 前言： “这个数据结构是属于比较抽象的一类。并且代码实现比较繁琐复杂。” 别人都这么说，我却觉得挺好理解、也挺好写的（可能是因为我曾经与多道线段树毒瘤题抗争多次）。 为了避免以后我突然脑子抽了不记得了，可以拿出来看看。所以写下这篇笔记，希望也能帮到大家。 建议：带上一个清晰的脑子（草 阅读全文

摘要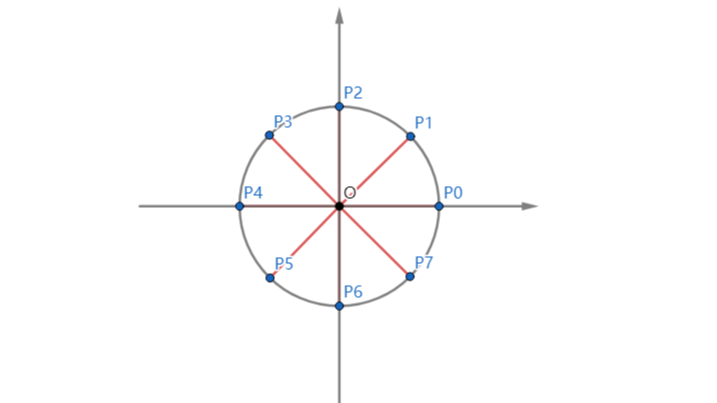： NTT 笔记 前言： 这个算法是与FFT 类似的，本片不会再从头讲起，建议先去补补课《FFT 笔记》。 本文只会讲一下互相关联的地方与一些不同的地方。 建议：在电脑前放好演算纸和笔。 注：本篇文章是我这个小蒟弱写的，真正的dalao请看个玩笑便好，不必争论对错（但是欢迎指出文章存在的小错误）。 NT 阅读全文

摘要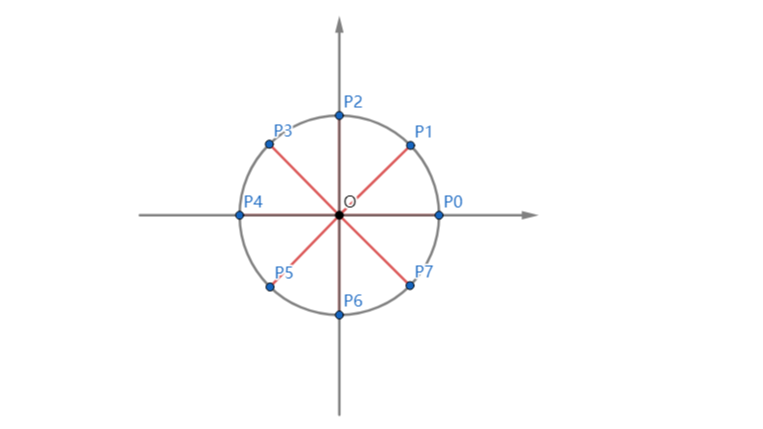： FFT笔记 前言： 这个算法对于我来讲比较抽象、高深，因为里面涉及了一些复数等一些对我而言很难很难的知识。 终于，花了几节文化课的时间冥思苦想，终于算是搞懂一点了。所以我决定趁脑子清醒的时候记录下来。 与其他文章不同的是，本文可能没有太多的公式证明，主要是以通俗易懂的方式去讲解，也是为了方便大家（包 阅读全文

摘要： T1 MIND 据题意，得 \[\sum_{i-1}^{n}{\frac{1}{n}\times\frac{1}{2^{\lceil\log_2\lceil\frac{k}{i}\rceil\rceil}}} \]其中\(\log_2\)可调用C++内置函数，\(2\)的阶乘可以用位运算. CODE 阅读全文