浅谈 AC 自动机
浅谈 AC 自动机
前言
这不是第一次看到这个算法。第一次是在 OI-wiki 上瞄到的。当时我还是一个什么也不懂的初一蒟蒻,看到这个名字就十分兴奋:“‘AC 自动机’耶!是不是可以帮我自动 AC !?”
后来看到只是一个字符串算法,就离开了。今天上课讲了这个,感觉原理及实现没有后缀数组那么难(还没做几道应用题)。趁一节晚修,来写篇笔记吧。
食用指南:要先学会 Trie树;KMP的话,理解到思想(\(\text{next}\) 数组)就可以了,不一定要学得透透的。
AC 自动机到底是什么?
AC 自动机是 以 Trie 的结构为基础,结合 KMP 的思想 建立的自动机。
之所以称为 AC 自动机,是因为此算法是由 Alfred V. Aho 和 Margaret J.Corasick 发明的,称为 Aho–Corasick 算法。
所以他不是 Automation,更不是 Accepted,而是 Automaton(自动机)。
AC 自动机可以用来干什么?
他是处理字符串的算法。
具体的,他可以解决多模式匹配的问题。
KMP 算法也是解决字符串匹配的,但他处理的问题只有一个模式串(需要寻找的串)和一个文本串(在这个串里寻找)。
而 AC 自动机,就可以解决多模式串匹配的问题。
算法思路
简单来说,建立一个 AC 自动机有两个步骤:
- Trie 结构:将所有的模式串构建成一棵 Trie 树。
- KMP 的思想:在 KMP 中,一旦失配,就跳到 \(\text{next}\) 失配指针所指的下一个字符;所以 AC 自动机中,也要对整颗 Trie 树所有节点构造失配指针。
那我们现在就开始吧。
Trie 树
回忆一下 AC 自动机的思路:首先把所有的字符串全部丢进 Trie 树里面,然后再在 Trie 树上构建自动机。
这个 Trie 树构建就很简单了,该怎么建就怎么建。详细内容可以看我的其他博客。
这里有一些需要理解的,就是一个节点到根节点的路径正是一个(或多个)模式串的前缀。
下文也把节点 \(x\) 到根节点的路径上的字符串称为状态 \(x\)。
失配指针
首先要明确一点:这里的“指针”并不是 C++ 中真正的“指针类型”,只是一个形象化的称号。
AC 自动机通过失配指针(下文称为 \(\text{fail}\) 指针)来辅助多模式串的匹配。
与 KMP 的 \(\text{next}\) 失配指针关系
- 相同点:两者同样是在失配的时候用于跳转的指针。
- 不同点:\(\text{next}\) 求的是最长的相同前后缀;而 \(\text{fail}\) 指针指向所有模式串的前缀中与当前节点“匹配”的“最长后缀”。
等等!这个“匹配”和这个“最长后缀”都是些什么东西?
先解释一下 \(\text{fail}\) 指针吧。
如果状态 \(x\) 的 \(\text{fail}\) 值是状态 \(y\),要求是:\(y\) 是 \(x\) 的最长后缀。
用人话说,就是:
先规定从节点 \(x\) 到根节点路径上形成的字符串为 \(\text{sub}(x)\);这个字符串中,第一个是根节点,最后一个是 \(x\) 节点上的字母。
如果 \(\text{sub}(y)\) 正好是 \(\text{sub}(x)\) 的后缀,并且不存在任意一个 \(\text{sub}(y')\) 的长度大于 \(\text{sub}(y)\) 的长度。
那么 \(\text{fail}(x)=y\)。
举个例子:
如果以
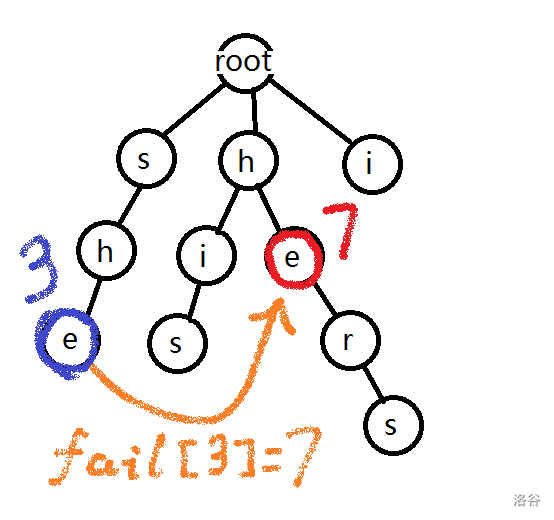
i,he,his,she,hers这些单词构建 \(\text{fail}\) 指针:
假设紫圈是 \(3\) 号节点,红圈是 \(7\) 号节点,那么 \(\text{fail}[3]=7\)。
因为
she的最长后缀(整棵 Trie 中)是he。
如果你看到这里,还是看不懂与KMP的区别,不要紧;你只需知道 AC 自动机的失配指针指向当前状态的最长后缀状态即可。
有一点提一下,AC 自动机在做匹配时,同一位上可匹配多个模式串。
构建 \(\text{fail}\) 指针
构建 \(\text{fail}\),可以参考 KMP 中构建 \(\text{next}\) 的思想。
假设字典树中当前节点为 \(u\),父节点为 \(fa\),并且 \(\text{sub}(u)=\text{sub}(fa)+c\)(记为 \(\text{trie}[fa,c]=u\))我们考虑深度比 \(u\) 小的节点的 \(\text{fail}\) 都已得到。
- 如果 \(\text{trie}[\text{fail}[fa],c]\) 存在,则 \(\text{fail}[u]=\text{trie}[\text{fail}[fa],c]\)。相当于分别在 \(fa\) 和 \(\text{fail}[fa]\) 下面加了一个字符 \(c\),分别对应 \(u\) 和 \(\text{fail}[u]\)。
- 如果 \(\text{trie}[\text{fail}[fa],c]\) 不存在,则继续寻找 \(\text{trie}[\text{fail}[\text{fail}[fa]],c]\)。重复 1 的判断,一直跳到根节点。
- 一直跳到了根节点都没有,那就让 \(\text{fail}[u]\) 指向根节点。
通过以上过程就可以完成 \(\text{fail}\) 的构建。
代码实现构建 \(\text{fail}\) 指针
尽管网上有许多实现方式,这里我们来看一下 OI-wiki 上的一种实现。
code
void build() {
for (int i = 0; i < 26; i++)
if (tr[0][i]) q.push(tr[0][i]);
while (q.size()) {
int u = q.front();
q.pop();
for (int i = 0; i < 26; i++) {
if (tr[u][i])
fail[tr[u][i]] = tr[fail[u]][i], q.push(tr[u][i]);
else
tr[u][i] = tr[fail[u]][i];
}
}
}
这里的 tr[u,c] 有两种理解方式:
- 字典树上的一条边,即 \(\text{trie}[u,c]\)。
- 状态(节点) \(u\) 后加一个字符 \(c\) 到达的新节点(状态)。
这里采用第 2 种方式讲解。
先讲一下这两行为什么这么写:
for (int i = 0; i < 26; i++)
if (tr[0][i]) q.push(tr[0][i]);
我们为什么是把根节点的儿子入队,而非直接把根节点入队呢?
试想一下,如果将根节点入队,那么第一次 bfs 的时候根节点儿子的 \(\text{fail}\) 指针就会指向自己。
常规 bfs 这里就不提及了,主要讲一下 for 循环中的 if 与 else 的“神仙实现”。
for 循环为什么这么写?——“神仙操作”,路径压缩
先解释一下代码最基础的意思:
- 如果
tr[u][i]存在,我们就将tr[u][i]的 \(\text{fail}\) 指针赋值为tr[fail[u]][i]。 - 否则,令
tr[u][i]指向tr[fail[u]][i]。
操作 1 貌似和上文讲的不太一样啊?——
根据上文,不应该是用 while 循环不停地跳、跳、跳 \(\text{fail}\) 指针,直到存在字符 i 对应的节点后再赋值吗?而且 else 里的操作直接改变了树的结构了呀?!!
其实这里做了一点“神仙处理”。
这个处理就是通过 else 改变字典树的结构。但值得注意的是,尽管我们将一个不存在的节点添加了一些指向关系,但是节点所代表的的字符串还是不变的。
由于 tr[S][c] 表示在 \(S\) 后增加一个字符 \(c\) 得到新字符串 \(S'\),这里要考虑 \(S'\) 是否存在。
- 存在,说明有某个模式串的前缀为 \(S'\)。
- 不存在,让
tr[S][c]指向tr[fail[S]][c]。这是因为fail[S]对应的字符串是 \(S\) 的后缀,那么tr[fail[S]][c]对应的字符串也就是 \(S'\) 的后缀。
但为什么可以这么写?
在 Trie 树上跳的时候,是从 \(S\) 跳到了 \(S'\);但是在 AC 自动机上,是从 \(S\) 跳到了 \(S'\) 的后缀。——因为 AC 自动机本质上是为了匹配,舍弃掉前面一些前缀也是可以匹配的,所以这里没有问题。
溯回本源,我们这个 Build() 说到底是在构建 \(\text{fail}\),现在我们来考虑一下 \(\text{fail}\) 是否也满足“舍弃前缀依然可匹配”这一推论。
显然可以,一旦文本串匹配 \(S\),自然能匹配 \(S\) 的后缀。所谓的 \(\text{fail}\) 指针其实是 \(S\) 的一个后缀集合。
什么?还是看不懂?其实还有一种简单粗暴的理解方式。
简单粗暴的理解
如果在位置 \(x\) 失配,我们跳到 \(\text{fail}[x]\)。因此有的时候需要跳、跳、跳很多次才能来到下一个匹配的位置。
所以我们可以用 tr 数组直接记录下一个能匹配的位置,以省时间。
本质上,与并查集路径压缩一样,这其实就是一种路径压缩。
“神仙操作”的好处
通过这种修改过后,匹配转移更加的完善,同时将 \(\text{fail}\) 指针跳转路径做了压缩。
这里本来想放图的,但是画出来很乱,不美观,所以建议去 OI-wiki 上看 gif(虽然也很乱,但起码比作者画得好)。
多模式匹配
代码实现
code
int query(char *t) {
int u = 0, res = 0, len = strlen(t + 1);
for (int i = 1; i <= len; i++) {
u = tr[u][t[i] - 'a']; // 转移
for (int j = u; j && e[j] != -1; j = fail[j]) {
res += e[j], e[j] = -1;
}
}
return res;
}
\(u\) 表示当前匹配到的节点,res 表示答案,e[j] 表示节点存储的信息(根据题目变化)。
循环遍历匹配串,\(u\) 则不断跟踪字符,利用 \(\text{fail}\) 指针找出所有匹配的模式串,累加到 res,然后标记已访问。
优化代码效率
这里可不是卡常,而是算法上的优化。
首先,大家可以去做一下 这道题。
发现会 T。这是因为在 AC 自动机中,每次匹配都会向 \(\text{fail}\) 边跳来找到所有的匹配。这样效率极低,即是路径压缩也没用。
考虑一下 \(\text{fail}\) 的性质:
一个 AC 自动机中,如果值保留 \(\text{fail}\) 边,剩余的图一定是一棵树。
这个很显然,因为 \(\text{fail}\) 不会成环,且深度一定比现在低。
AC 自动机的匹配就可以转化成在 \(\text{fail}\) 树上的链求和问题了。
这里介绍拓扑排序。
拓扑排序优化建图
原来时间都浪费在“跳 \(\text{fail}\)”上了。如果预先记录,最后一并求和,那么效率就会被优化。
代码实现中,不需要真正的建图,记录入度就可以了。
查询操作也只需要给找到的节点的 ans 打标记,最后拓扑排序求答案就好了。
建图实现
code
void getfail() // 实际上也可以叫 build
{
for (int i = 0; i < 26; i++) trie[0].son[i] = 1;
q.push(1);
trie[1].fail = 0;
while (!q.empty()) {
int u = q.front();
q.pop();
int Fail = trie[u].fail;
for (int i = 0; i < 26; i++) {
int v = trie[u].son[i];
if (!v) {
trie[u].son[i] = trie[Fail].son[i];
continue;
}
trie[v].fail = trie[Fail].son[i];
indeg[trie[Fail].son[i]]++; // 修改点在这里,增加了入度记录
q.push(v);
}
}
}
查询实现
void query(char *s) {
int u = 1, len = strlen(s);
for (int i = 0; i < len; i++) u = trie[u].son[s[i] - 'a'], trie[u].ans++;
}
void topu() {
for (int i = 1; i <= cnt; i++)
if (!indeg[i]) q.push(i);
while (!q.empty()) {
int fr = q.front();
q.pop();
vis[trie[fr].flag] = trie[fr].ans;
int u = trie[fr].fail;
trie[u].ans += trie[fr].ans;
if (!(--indeg[u])) q.push(u);
}
}
主函数
int main() {
// do_something();
scanf("%s", s);
query(s);
topu();
for (int i = 1; i <= n; i++)
cout << vis[rev[i]] << std::endl;
// do_another_thing();
}
完整代码就不挂了,洛谷题解区有一堆。
参考文献
- [1] OI-wiki,《AC 自动机》
- [2] DengDuck,《AC 自动机 ACAM 学习笔记》
结尾
一节晚修写完,除了板题,其他的题还没做,作者溜去做题了。
如有侵权,联系作者解决。
希望能帮到你,Thank you!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号