大神之路-起始篇 | 第4章.计算机科学导论之【数据运算】学习笔记

[ 点击 👉 关注「 全栈工程师修炼指南」公众号 ]

设为「⭐️ 星标」带你从基础入门 到 全栈实践 再到 放弃学习！
涉及 网络安全运维、应用开发、物联网IOT、学习路径 、个人感悟 等知识分享。

希望各位看友多多支持【关注、点赞、评论、收藏、投币】，助力每一个梦想。

【WeiyiGeek Blog's - 花开堪折直须折，莫待无花空折枝 】
作者主页: 【 https://weiyigeek.top 】
博客地址: 【 https://blog.weiyigeek.top 】
作者答疑学习交流群：欢迎各位志同道合的朋友一起学习交流【点击 👉 加入交流群】, 或者关注公众号回复【学习交流群】。

目录

计算机科学导论学习笔记

前言：当前作为一名IT互联网从业者，计算机技术日新月异，每天都有新概念、新技术的出现，而像我这样的万金油来说，越学到后面就越吃力，遇到瓶颈问题也随之增多，因为本身非科班出身，加之半路出家，针对于计算机基础知识掌握不牢或者说是不完整，所以我痛定思痛，下定决心重新学习计算机相关基础知识，从计算机科学导论，到计算机组成原理，到计算机网络、到操作系统，到数据结构，到程序算法、到应用开发、到安全运维开发。

今天 (2022年9月1日) 便从大神之路-起始篇,我们要站在巨人们的肩膀上，进行计算机科学导论的 学习，我将总结学习成果笔记，帮助后续入门学习的朋友。

随着现代计算机的发明，带来了新的学科，即计算机科学（简称计科）一词上一个非常广泛的概念，在此处我没将其定义为计算机相关的问题，现在计算机科学被划分成几个领域，总结归纳为两大类系统领域和应用领域.

  • 系统领域：涵盖那些与硬件和软件构成直接有关的领域，例如计算机体系结构、计算机网络、安全问题、操作系统、算法、程序设计语言以及软件工程。
  • 应用领域：涵盖了与计算机使用有关的领域，例如数据库、云物联和人工智能。

参考书籍:【计算机科学导论-第三版 （Foundations Of Computer Science - Third Edition) 】作者： [美] 贝赫鲁兹.佛罗赞 (Behrouz Forouzan) PS: 当下已经第四版了、

参考视频：【计算机导论】计算机科学导论（大神之路-起始篇）

第 2 部分 数据的表示和运算

描述：该部分包括第2、3和4章，我们分别进行如下学习。

  • 第2章讨论了数字系统，数量如何能使用符号来表示。

  • 第3章讨论了不同的数据如何存储在计算机中。

  • 第4章讨论了一些基本的算术运算与位(逻辑)运算。

原文地址: https://mp.weixin.qq.com/s/0LaYhi89ujYQPHuLfwnuiA

4.数据运算

主要讲解存储在计算机中的数据上是如何进行运算，数据的运算可以分为三大类：算术运算、移位运算和逻辑运算。

4.1 逻辑运算

计算机中的数据是以位模式存储的，逻辑运算是指那些应用于模式中的一个二进制位，或在两个模式中相应的两个二进制位的相同基本运算，说人话就是分别针对二进制位进行与、或、非、异或等操作。

意味着我们可以在位层次上和模式层次上定义逻辑运算，模式层次上的逻辑运算是具有相同类型的位层次上的n个逻辑运算，这里的n就是模式中的位的数目。

(1) 位层次上的逻辑运算

一个位可能是0或1,可以假设“0”代表逻辑“假”，而“1”代表逻辑“真”，我们可以应用布尔代数中定义的运算去操纵二进制位为纪念乔治•布尔（George Boole）而命名的布尔代数属于逻辑的特殊数学领域.

与、或、非、异或

  • 逻辑 与 (AND) 运算: 常用运算符&表示, 只要一假都为假, 即参与运算的两个值,如果两个相应位都为1,则该位的结果为1,否则为0。

  • 逻辑 或 (OR) 运算：常用运算符|表示, 只要一真都为真, 即只要对应的二个二进位有一个为1时，结果位就为1。

  • 逻辑 非 (NOT) 运算：常用运算符!表示, 一假变一真，一真变一假, 即一个二进制位为1在进行非运算后结果为0，反之为0时经过非运算后结果为1。

  • 逻辑 异或 (XOR) 运算 (发音为“ exclusive-or”)：常用运算符^表示, 真假为真，真真为假，假假也为假, 即当两对应的二进位相异(分别为0、1)时其结果为1。

    XOR 运算符并不是一个新的运算符，其只是 AND 、OR 、NOT 运算符的组合。

    例如 x XOR y = [ x AND (NOT y) ] OR [ (NOT x) AND y ]

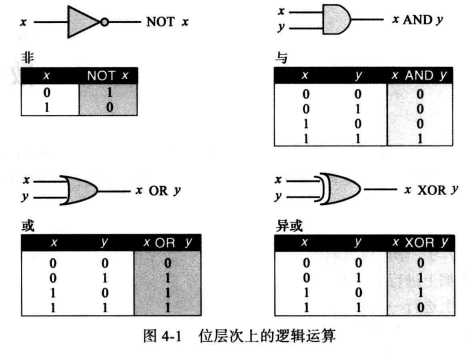
WeiyiGeek.位运算真值表

例如，与、或、非、异或位逻辑运算示例

# 逻辑 或 运算 (一真必真)
真：1 & 1 = 1
假：0 & 0 = 0, 0 & 1 = 0, 1 & 0 = 0

# 逻辑 与 运算 (一假必假)
真：1 | 1 = 1, 0 | 1 = 0, 1 | 0 = 0
假：0 | 0 = 0,

# 逻辑 非 运算 (一真一假)
真：!0 = 1 
假：!1 = 0

# 逻辑 异或 运算 （真假必真）
真：1 ^ 0 = 1, 0 ^ 1 = 1
假：0 ^ 0 = 0, 1 ^ 1 = 0

(2) 位模式层次上的逻辑运算

相同的4个运算符（NOT、AND、OR和XOR）可以被应用到n位模式，效果就是对NOT运算来说，把每个运算符应用于每个位，对于其他3个运算符就是把每个运算符应用于相应的位对，有点云里雾里，看了这个例子你就明白了，例如对 10011000 二进制进行 NOT 逻辑运算，将其每个二进制位进行取反则结果为 01100111 。

例如，与、或、非、异或位模式逻辑运算示例

# 1.NOT(非运算符)来计算位模式 10011000
NOT 1 0 0 1 1 0 0 0  | 输入
    0 1 1 0 0 1 1 1  | 输出
    
# 2.AND(与运算符)来计算位模式 10011000 和 00101010
    1 0 0 1 1 1 0 0  | 输入1
AND 0 0 1 0 1 0 1 0  | 输入2
    0 0 0 0 1 0 0 0  | 输出
    
# 3.OR(或运算符)来计算位模式 10011000 和 00101010
    1 0 0 1 1 1 0 0  | 输入1
OR  0 0 1 0 1 0 1 0  | 输入2
    1 0 1 1 1 1 1 0  | 输出
    
# 4.XOR(异或运算符)来计算位模式 10011000 和 00101010    
    1 0 0 1 1 1 0 0  | 输入1
XOR 0 0 1 0 1 0 1 0  | 输入2
    1 0 1 1 0 1 1 0  | 输出

四种逻辑运算的应用

  • 求反：NOT运算符的唯一应用就是对整个模式求反。
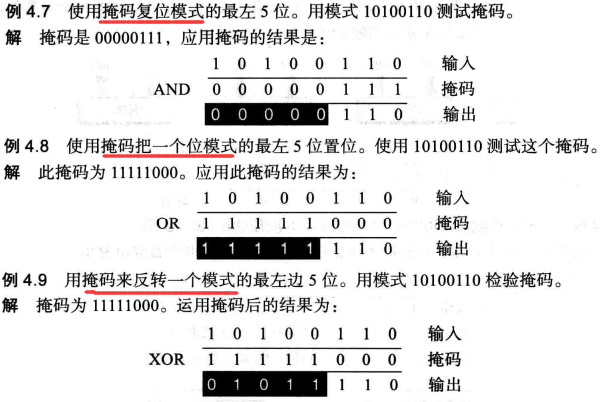
  • 使指定的位复位：AND运算的一个应用就是把一个位模式的指定位进行复位（置0），通常叫做掩码复位模式.
  • 对指定的位置位：OR运算的一个应用是把一个位模式的指定位进行置位（置1）.
  • 使指定的位反转：XOR运算的针对位模式中指定的位进行反转（求反）。

WeiyiGeek.掩码位模式

为防止伸手党，付费完整原文，请各位看友多多支持： https://mp.weixin.qq.com/s/0LaYhi89ujYQPHuLfwnuiA

原文地址: https://blog.weiyigeek.top/2022/6-2-695.html

本文至此完毕，更多技术文章，尽情期待下一章节！

专栏书写不易，如果您觉得这个专栏还不错的，请给这篇专栏 【点个赞、投个币、收个藏、关个注，转个发，留个言】(人间六大情)，这将对我的肯定，谢谢！。

点击 👉 关注「 全栈工程师修炼指南」公众号
微信沟通交流: weiyigeeker (点击添加)
交流沟通群：629184198 或 关注公众号回复【学习交流群】

温馨提示: 由于作者水平有限，本章错漏缺点在所难免,希望读者批评指正，并请在文章末尾留下您宝贵的经验知识，联系邮箱地址 master@weiyigeek.top 或者关注公众号 WeiyiGeek 联系我。

帅哥（靓仔）、美女，点个关注后续不迷路

posted @ 2023-04-07 09:32  全栈工程师修炼指南  阅读(42)  评论(0)  编辑  收藏  举报