剑指Offer的学习笔记(C#篇)-- 平衡二叉树(二叉树后序遍历递归详解版)
题目描述
输入一棵二叉树,判断该二叉树是否是平衡二叉树。
一 . 题目分析
首先要理解一个概念:什么是平衡二叉树,如果某二叉树中任意的左右子树深度相差不超过1,那么他就是一颗平衡二叉树。如下图:
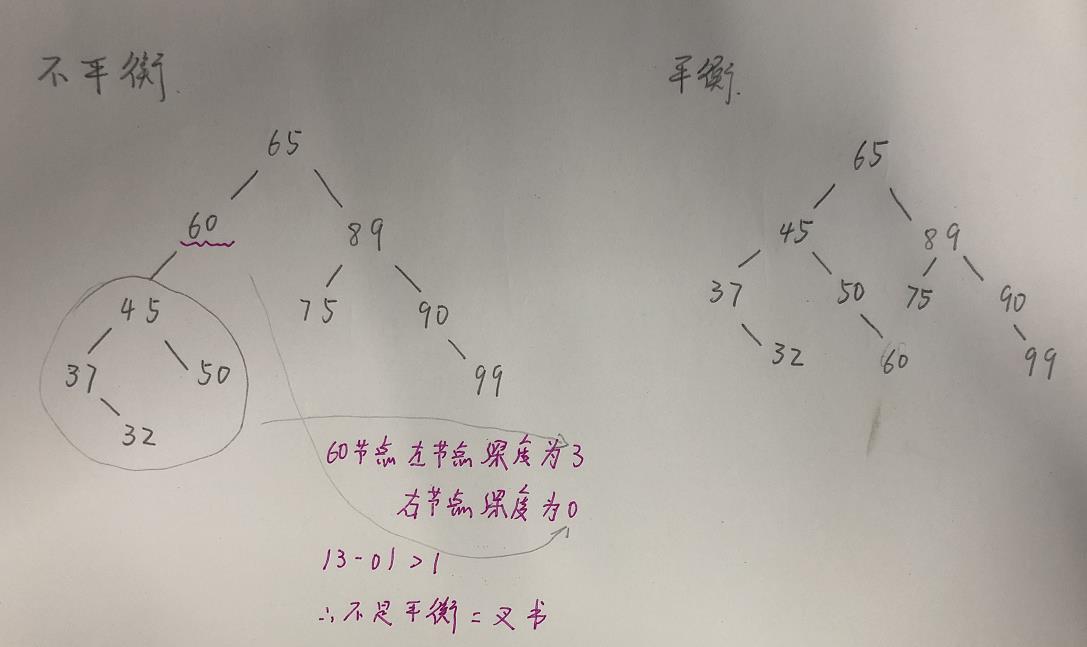
所以,知道了这个概念之后,回归题目。判断该二叉树是不是平衡二叉树,就要在二叉树每个节点的深度来搞了,肯定要对二叉树进行遍历,但是如何效率最大化,如果从小往上遍历,一次遍历是否可以完成任务,而从下往上的遍历又让我想到了二叉树唯一的一种自下而上的遍历方法(我说的仅是前后根三种之中而已)。
解决方案与关键词:
1 . 二叉树自下而上遍历一次:后序遍历,左右根
2 . 二叉树平衡判断条件:每个根节点深度绝对值小于等于1
3 . 二叉树每个根节点的深度累加:递归实现
二 . 代码实现
class Solution { public bool IsBalanced_Solution(TreeNode pRoot) { // write code here // 若为空树,返回正确 if (pRoot == null) return true; // 递归函数 getNextDepth(pRoot); // 最终结果 return valid; } // 定义一个初始值假设该树是平衡二叉树 bool valid = true; private int getNextDepth(TreeNode node) { // 若为空树,判断深度 if (node == null) { return 0; } else { // 左右递归 int left = getNextDepth(node.left); int right = getNextDepth(node.right); // 平衡二叉树的判断条件(左右节点差小于等于1) if ((left - right) > 1 || (right - left) > 1) { valid = false; } // 二叉树深度累加方法,目的用于上一段代码进行深度判断 int res = 1 + System.Math.Max(left, right); return res; } } }
三 . 用通俗的语言进行代码详解
依旧用举例的方法进行,如下图:
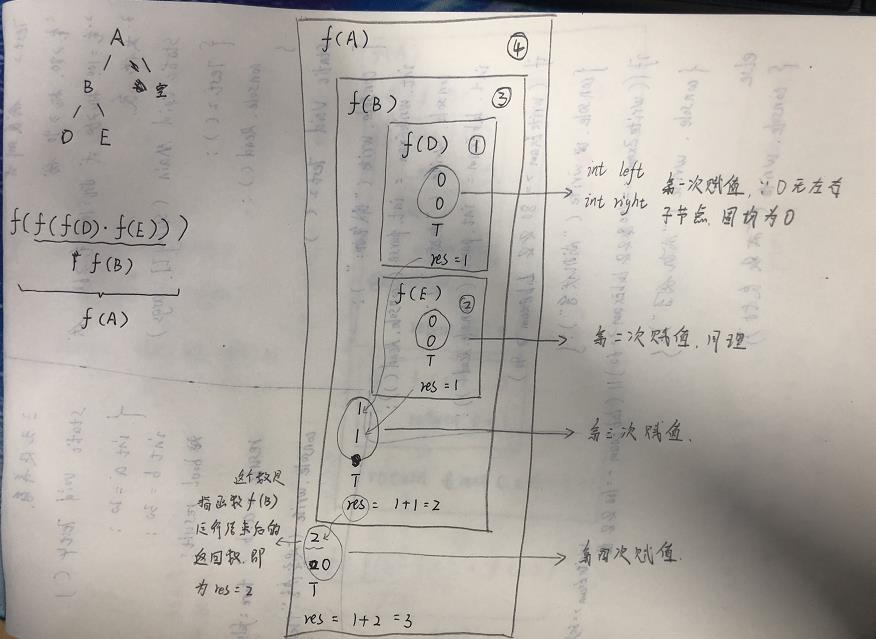



 浙公网安备 33010602011771号
浙公网安备 33010602011771号