剑指Offer的学习笔记(C#篇)-- 二叉搜索树的后序遍历序列
题目描述
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
一 . 解题思想与二叉搜索树概念
(1). 二叉树的后序遍历方法(左→右→根)。
(2). 二叉查找树,又被称为二叉搜索树。其特点如下:设x为二叉查找树中的一个结点,x节点包含关键字key,一句话就是左孩子比父节点小,右孩子比父节点大,还有一个特性就是”中序遍历“可以让结点有序。看下图,解释一下:
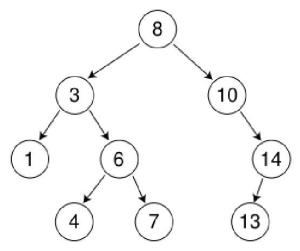
可以看出,在二叉树中:
- 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点,同一个父节点的两个同层的节点,左小于右。
二 . 解题思路
(1). 通过取出序列最后一个元素得到二叉搜索树的根节点;
(2). 在二叉搜索树中左子树的结点小于根结点,因此可以遍历一次得到左子树;
(3). 在二叉搜索树中右子树的结点大于根结点,因此可以继续遍历后序元素得到右子树;
(4). 重复以上步骤递归判断左右子树是不是二叉搜索树,如果都是,则输入yes,如果不是,则输出no;
三 . 代码实现
class Solution { public bool VerifySquenceOfBST(int[] sequence) { // write code here if(sequence.Length == 0) { return false; } return Verify(sequence, 0, sequence.Length-1); } public bool Verify(int[] sequence, int start, int end) { int root = sequence[end]; int i = start; for(; i<end; i++) { if(sequence[i] > root) break; } int j = i; for(; j<end; j++) { if(sequence[j] < root) return false; } bool left = true; if(i-1 > start) { left = Verify(sequence, start, i-1); } bool right = true; if(i < end-1) { right = Verify(sequence, i, end-1); } return (left && right); } }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号