剑指Offer的学习笔记（C#篇）-- 矩形覆盖

题目描述

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

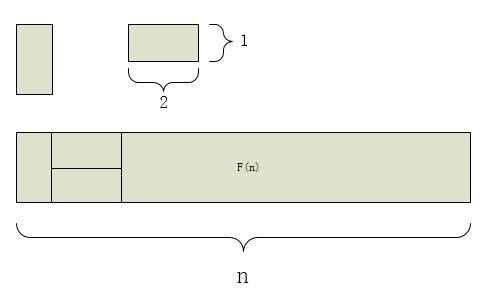
一 . 解题思路

        这个貌似就是普通的跳台阶问题。

二 . 代码实现

方法一：递归法

class Solution {
    public int rectCover(int number)
       {
            if(number <= 0)
            {
                return 0;
            }

            if(number == 1)
            {
                return 1;
            }

            if(number == 2)
            {
                return 2;
            }

            return rectCover(number - 1) + rectCover(number -2 );

      }
}

方法二：循环法

class Solution
{
    public int rectCover(int number)
    {
        // write code here
        int sum = 0;
        int a=1,b=2;
        if (number == 1)
        {
            sum = 1;
        }
        else if (number==2)
        {
            sum = 2;
        }
         else
         {
            for (int i = 3; i <=number; i++)
               {
                 sum = a + b;
                 a = b;
                 b = sum;
               }
         }
         return sum;
    }
}

 题目延伸：

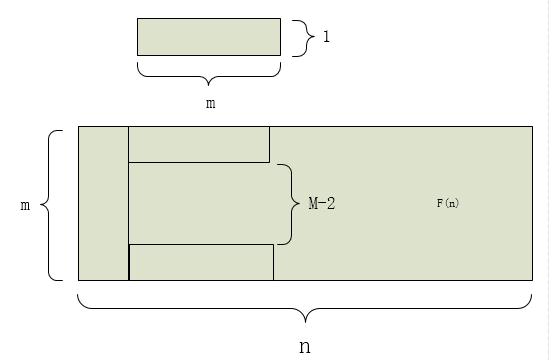
如果将题目改成1*3方块覆盖3*n、1*4方块覆盖4*n。

相应的结论应该是：

（1）1 * 3方块 覆 盖3*n区域：f(n) = f(n-1) + f(n - 3)， (n > 3)

（2） 1 *4 方块 覆 盖4*n区域：f(n) = f(n-1) + f(n - 4)，(n > 4)

更一般的结论，如果用1*m的方块覆盖m*n区域，递推关系式为f(n) = f(n-1) + f(n-m)，(n > m)。

number