剑指Offer的学习笔记（C#篇）-- 变态跳台阶

题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

一 . 解题思路。

        该题目为跳台阶题目的延伸，普通跳台阶每次跳的阶数（1或2），而该题目每次跳的阶数进化为（1~N），其实万变不离其宗，看下图：

 

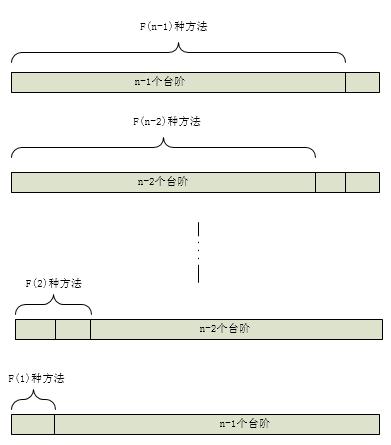
        其实想法和普通跳台阶完全一致，跳1级，剩下n-1级，则剩下跳法是f(n-1)，跳2级，剩下n-2级，则剩下跳法是f(n-2)，所以f(n)=f(n-1)+f(n-2)+...+f(1)，因为f(n-1)=f(n-2)+f(n-3)+...+f(1)，所以f(n)=2*f(n-1)。老实说，这里有点绕，我表示不是很清楚，普通跳台阶解题思路点这里。该题目也是递归与循环的基础使用。

二 . 代码实现

方法1：递归法

class Solution
{
    public int jumpFloorII(int n)
    {
        if(n < 0)
        {
            return -1;
        }
         else if(n == 0 || n == 1)
        {
            return 1;
        }
        else
        {
            return 2*jumpFloorII(n-1);
        }
    }
}

方法2：循环法

class Solution
{
    public int jumpFloorII(int n)
    {
        if (n<=2) return n;
        int result=0;
        int result1=1;
        int result2=2;
        for(int i=3;i<=n;i++)
        {
            result=result1+result2+1;
            result1=result1+result2;
            result2=result;
        }
        return result;
    }
}