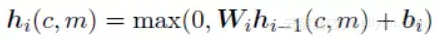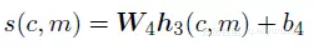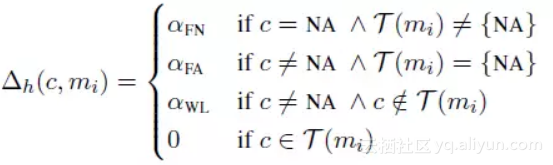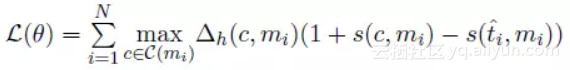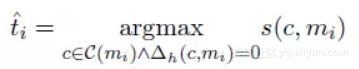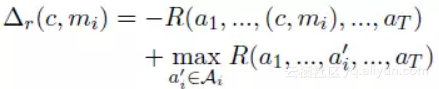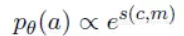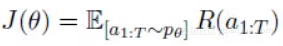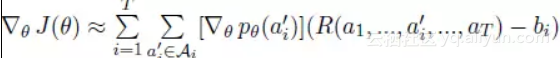深度强化学习在指代消解中的一种尝试

本文出自斯坦福 NLP 组，发表在 EMNLP 2016，其将深度强化学习应用于指代消解领域是一大创新，相较于其他方法有很好的效果提升。

指代消解是自然语言处理的一大研究领域，常见的指代消解算法多数模型采用启发式损失函数，不同消解任务为达到良好的使用效果需要对调整损失函数超参数。

常见的指代消解算法有 Mention Pair、Mention Rank、Entity Mention 等等，本文将深度强化学习应用于 Mention Rank 实现消解技术的通用性，解决启发式损失函数的超参微调问题。

模型介绍

论文作者将其发表于 ACL 2016 的 Neural Mention-ranking 模型 [1] 进行强化学习的改进。

模型结构

如下图所示，Neural Mention-ranking 模型结构主体部分为多层的前反馈神经网络，分为三个部分：首先是输入层将指代词（mention）特征、候选前指词（Candidate Antecedent）即指代词出现前的词特征、指导词所在句子特征以及其他特征例如距离特征、连接关系特征等等做向量拼接（concate）处理作为模型的输入 h0。

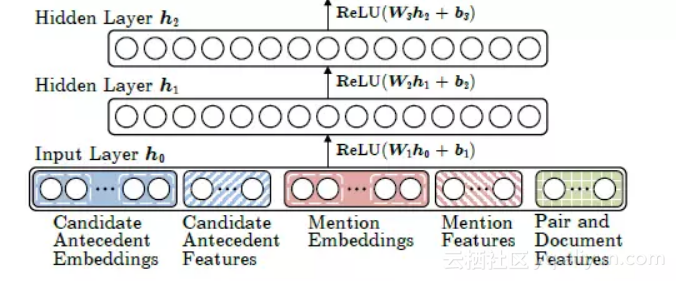
特征的获取过程不是本论文的重点，这里不详细阐述，对特征如何获取感兴趣可以参考 [1]。

隐藏层采用 Relu 作为激活函数，其中隐藏层共 3 层，其公式定义如下：

分数获取层，其采用基本的线性相乘法，公式定义如下：

启发式损失函数

Neural Mention-ranking 模型结构采用一种启发式 Max-Margin 损失函数，Max-Margin 即 Hinge Loss 的一种变种。 首先，先看松弛参数 △h 的定义。

其中 C(mi) 表示预测的候选前指词库，T(mi) 表示真实的前指词库，c∈C(mi)，NA 表示为空，FN、FA、WL 依次表示“不为空”、“错误的前指”、“错误连接”。 损失函数定义如下，该函数目的是让真实的前指词“分数”更高，错分情况“分数”随着训练不断降低。

其中 ti 表示预测候选词中真实前指词的最高“分”（Score），定义如下。

参数 ɑ 的定义采用人工微调的方式，不断尝试，最终确定最优值。

强化学习对损失函数的改进

论文采用两种强化学习方式改进，一种对超参数的改进，采用强化学习的奖励机制，另一种采用经典的增强策略梯度算法。

论文中将 Neural Mention-ranking 模型当做代理（agent），而每个行为 ai 表示第 i 个指代词的其中一个前指词。Ai 表示第 i 步中所有的候选行为集合即所有第 i 个指代词的所有候选词集合。奖励函数 R(a1:T) 表示第 1 个行动到最后行动的奖励，用 B-cubed 函数 [2] 表示。

1. 奖励衡量机制

这种方式将上述启发式损失函数的松弛参数 △ 进行改进，由于没个行为都是没有关联性、独立的，因此可以通过尝试不同的行为判断每一步奖励差异。因此松弛参数变化如下所示。

这种机制的训练方式和启发式损失函数一致。

2. 经典强化学习方式

除上述奖励衡量机制外，采用经典的增强策略梯度算法，每个行为 a=(c,m) 的概率定义如下。

损失函数定义如下：

为使获得奖励值最大，采用梯度上升法进行参数更新，由于每一次行为选择随着句子的增长指数级增长，因此梯度值计算困难。论文采用一种梯度估值，定义如下所示。

模型实验效果

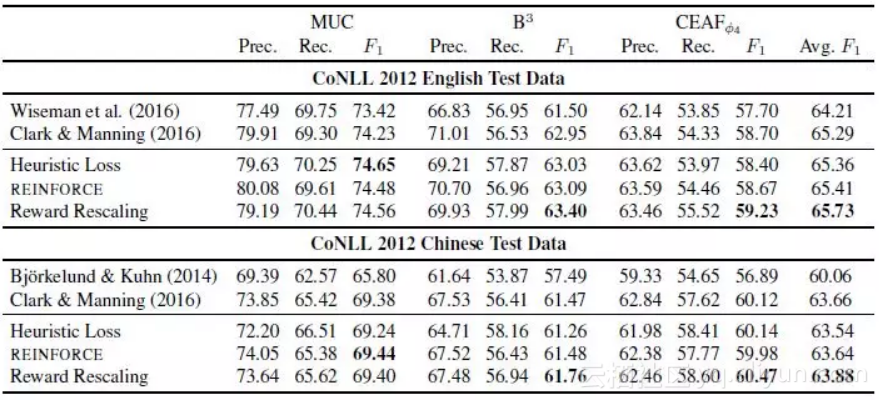
通过对 CoNLL2012 的英文和中文的指代数据实验，得到测试结果如下图所示，奖励衡量机制效果明显，表现最佳

论文评价

这篇论文发表于 2016 年的 EMNLP，尝试对指代消解的一种神经网络 Mention Rank 模型的启发式损失函数中的超参数利用强化学习方式进行优化，提出一种奖励衡量机制，跟其他方式比效果突出。

这种基于强化学习的奖励衡量机制的超参数调节方式会对很多研究工作产生启发，特别是对超参设置采用尝试性遍历方式的研究工作。可惜论文发表到现在两年时间，在指代消解中利用强化学习的方式没有更好的新的尝试。

 

原文发布时间为：2018-05-17

本文作者：姜松浩

 

本文来自云栖社区合作伙伴“PaperWeekly”，了解相关信息可以关注“PaperWeekly”。