SPFA 判负环
SPFA 判负环
大家好，我是Weekoder！
今天我要讲的是接上一次 SPFA 最短路算法衍生而来的一个应用——判断图中是否存在负环。我将介绍两种判负环的方法，都基于 SPFA。
负环的概念
负环是什么？
负环就是在图中的一个环，其边权之和为负数。如下图：
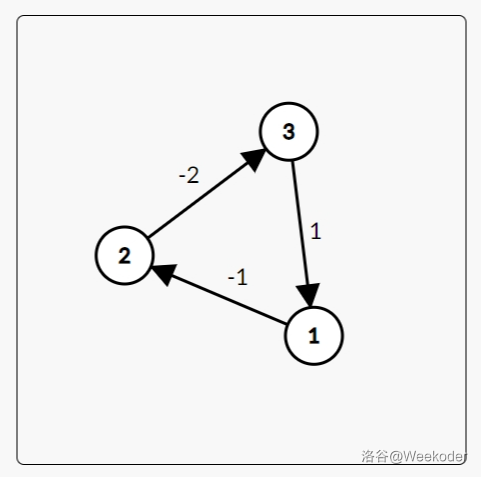
可以看到，这个环的权值和是 \((-2)+(-1)+1=-2\)，为负数，则这是一个负环。哪怕其中有正权值，只要权值和小于 \(0\)，这个环即是一个负环。
如果一个图有负环，则该图没有最短路，因为可以在负环中无限绕圈，不断减少路径长度，一直到 \(-\infty\)。
BFS-SPFA 判负环
今天介绍的第一种方法是基于 BFS 的搜索方式的判定方法。在 SPFA 模板的基础上，只修改了一点点，非常容易。它的原理是：维护一个 \(dp\) 数组用于计数，\(dp_i\) 表示点 \(i\) 的最短路所经过的边数。我们知道一个点的最短路最多会经过其他 \(n-1\) 个点。经过多少点，就经过多少边，则我们有：\(dp_i\le n-1\)。我们不会经过任何一个重复的点，除非有负环让这个点继续走下去。那么当上一个式子 \(dp_i\le n-1\) 反过来，就变成了 \(dp_i>n-1\)，即 \(dp_i\ge n\)，也就是重复走了一个点，有负环。于是我们可以状态转移，对于一条边 \(cut\to nxt\)，我们的状态转移方程是：\(dp_{nxt}=dp_{cur}+1\)。然后我们再判断 \(dp_i\ge n\)，如果成立则有负环，最后返回没有负环。虽然讲了一大堆，但是代码却几乎没有修改。
参考题目：P3385。
\(\text{Code:}\)
bool spfa(int s) {
queue<int> q;
memset(dis, 0x3f, sizeof dis);
memset(vis, 0, sizeof vis);
memset(dp, 0, sizeof dp); // 记得初始化
dis[s] = 0;
vis[s] = 1;
q.push(s);
while (!q.empty()) {
int cur = q.front(); q.pop();
vis[cur] = 0;
for (auto nxt : nbr[cur]) {
int to = nxt.to, w = nxt.w;
if (dis[to] > dis[cur] + w) {
dis[to] = dis[cur] + w;
dp[to] = dp[cur] + 1; // 状态转移方程
if (dp[to] >= n) return 1; // 如果存在负环，则返回1
if (!vis[to]) {
vis[to] = 1;
q.push(to);
}
}
}
}
return 0;
}
DFS-SPFA 判负环
这个方法是我在做 P3199 最小圈的时候，因为不知道为什么 \(\color{#052242}\texttt{TLE}\) 而去网上查到的（好了，P3199 就是下一篇文章的素材了）。它的原理也很简单，就是一个点如果被松弛多于 \(1\) 次，就一定存在负环。在一开始，就给当前的点打上 \(\text{vis}\) 标记，最后再取消。我们遍历当前点的邻接点，假设为 \(\text{to}\)。在松弛完毕后立马判断 \(\text{vis}_\text{to}\) 是否为 \(\text{True}\)，如果是，则 \(\text{to}\) 之前就被松弛过，现在还能松弛，则一定有负环。否则继续 \(\text{DFS}\)，最后返回 \(\text{False}\)。如果递归的结果是 \(\text{True}\)，则也有负环，可以写为一个条件判断式，即 \(\text{vis}_\text{to}||\text{spfa(to)}\)。这里有个细节，\(\text{vis}_\text{to}\) 写在前面，因为短路运算符的性质，只要 \(\text{vis}_\text{to}\) 成立，就不会看 \(\text{spfa(to)}\)，不再继续 \(\text{DFS}\)，节省时间。
\(\text{Code:}\)
bool spfa(int cur) {
vis[cur] = 1;
for (auto nxt : nbr[cur]) {
int to = nxt.to, w = nxt.w;
if (dis[to] > dis[cur] + w) {
dis[to] = dis[cur] + w;
if (vis[to] || spfa(to)) return 1;
}
}
vis[cur] = 0;
return 0;
}
可以看到，\(\text{DFS}\) 的代码简短的多，但是友情提示一下，这个算法过不了 P3385，会 T 一个点。
BFS-SPFA 对比 DFS-SPFA
如果你去实践了一下，你会发现：诶？DFS 的版本过不了模板，BFS 却能过。DFS 是不是比 BFS 慢？不，听我来分析一下他们的区别。DFS-SPFA 其实比 BFS-SPFA 要快得多。你会发现评测记录中其他测试点基本上都是几毫秒，都没有超过 \(10\text{ms}\)。在一个图中，如果只要判断是否存在负环，DFS-SPFA 是非常快的，这道模板题只是有一个点专门卡 DFS。而如果要在没有负环后输出最短路，则 BFS 会更快。比如下一次要讲的一些习题中，有的就要获得最短路，而有的只要判断负环存在就行了。比如我说的 P3199 最小圈，就只要判断是否存在负环，用 BFS-SPFA 就会 \(\color{#052242}\texttt{TLE}\) 挂 \(50\text{pts}\)。
小结
综上所述，SPFA 判负环的方法就是这些了。请不要忘记关注下一次的文章：负环的习题和应用。
