9.队列：生产者消费者模式

队列：生产消费模式及线程池的运用

关注公众号 MageByte，设置星标获取最新干货。 “加群” 进入技术交流群获更多技术成长。

向固定大小的线程池投放请求任务时，若果线程池中没有空闲资源了，这时候还有新的请求进来，线程池如何处理这个请求？拒绝请求还是排队？使用怎样的处理机制

一般两种策略：

直接拒绝任务请求；
将请求排队，等有空闲线程的时候取出排队的请求继续处理。

那如何存储排队的请求呢？这就是今天要讲的话题。

其底层的数据结构就是今天我们要讲的内容，「队列」Queue。

完整代码详见 GitHub：https://github.com/UniqueDong/algorithms.git

什么是队列

用一个生活例子，可以想象成超市排队结账，先来的先结账，后面的人只能站在末尾，不允许插队。先进先出，这就是所谓的「队列」

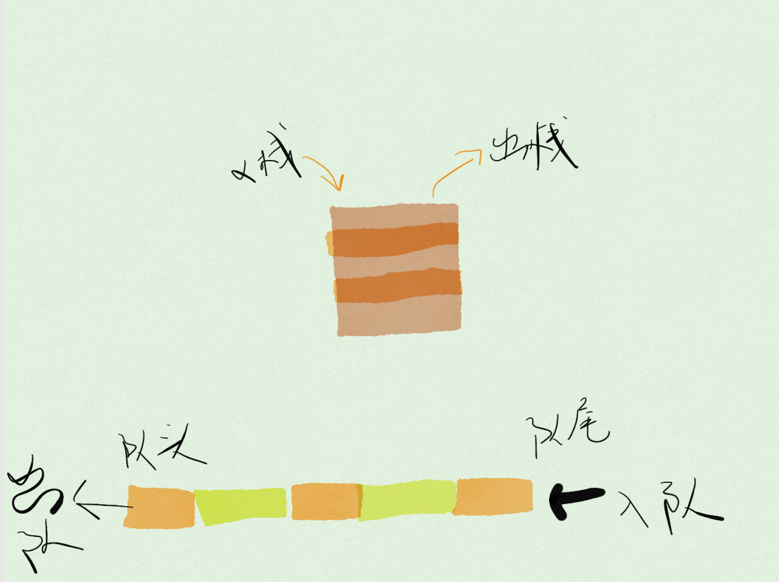
队列是一种线性数据结构，队列的出口端叫「队头」，队列的入口端叫「队尾」。

与栈类似队列的数据结构可以使用数组实现也可以使用链表实现。关于栈的内容同学们可以翻阅历史文章学习「栈：实现浏览器前进后退」，队列最基本的操作也是两个：入队 (enqueue) ，将新元素放到队尾；出队 (dequeue)，从队头移除元素，出队元素的下一个元素变成新的队头。

作为基础的数据结构，队列的应用也很广泛，尤其是一些特定场景下的队列。比如循环队列、阻塞队列、并发队列。它们在很多偏底层系统、框架、中间件的开发中，起着关键性的作用。比如高性能队列 Disruptor、Linux 环形缓存，都用到了循环并发队列；Java concurrent 并发包利用 ArrayBlockingQueue 来实现公平锁等。

队列与栈

队列也是一种操作受限的线性表数据结构。

顺序队列与链式队列

队列是跟栈一样，是一种抽象的数据结构。 具有先进先出的特性，在队头删除数据，在队尾插入数据。

可以使用数组实现，也可以使用链表实现。使用数组实现的叫 顺序队列，用链表实现的叫 链式队列。

顺序队列

一起先来看数组实现的队列：

出队操作就是把元素移除队列，只允许在队头移除，出队的下一个元素成为新的队头。
入队操作就是把新元素放入队列，只允许在队尾插入，新元素的的下一个位置成为队尾。

随着不停地进行入队、出队操作，head 和 tail 都会持续往后移动。当 tail 移动到最右边，即使数组中还有空闲空间，也无法继续往队列中添加数据了。这个问题该如何解决呢？

当出现这种情况的时候我们就需要做数据迁移。如图所示：当 abcd 入队后，对应的指针位置。

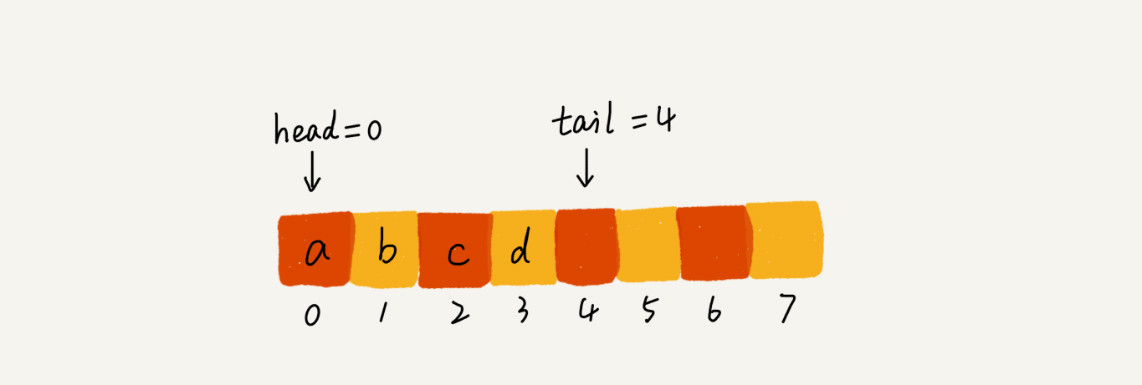
现在我们执行出队操作

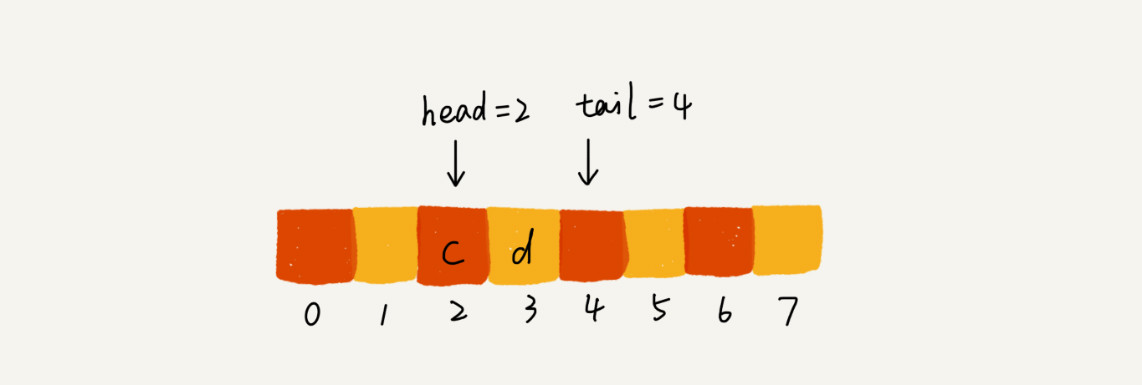
当我们调用两次出队操作之后，队列中 head 指针指向下标为 2 的位置，tail 指针仍然指向下标为 4 的位置。

迁移操作其实就是把整段数据移动到数组 0 开始的位置。

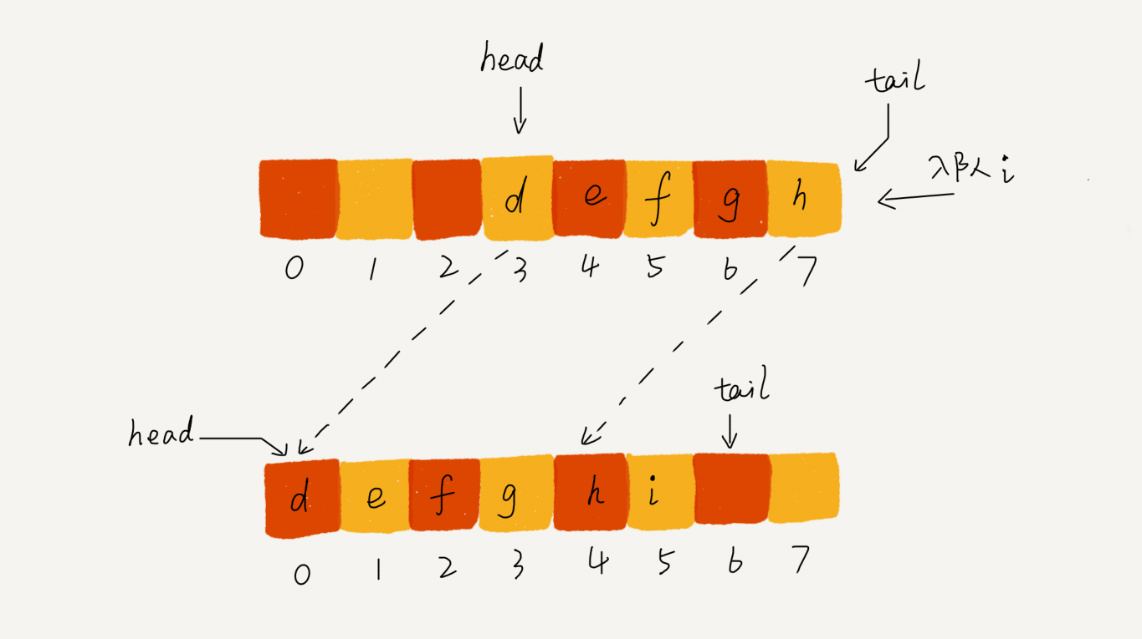
具体代码如下

/**
 * 数组实现队列
 */
public class ArrayQueue<E> extends AbstractQueue<E> {
    /**
     * The queued items
     */
    final E[] items;
    /**
     * 队头指针
     */
    private int front;

    /**
     * 队尾指针
     */
    private int rear;

    /**
     * Creates an ArrayQueue with the given capacity
     *
     * @param capacity the capacity of this queue
     */
    public ArrayQueue(Class<E> type, int capacity) {
        if (capacity <= 0) {
            throw new IllegalArgumentException();
        }
        this.items = (E[]) Array.newInstance(type, capacity);
    }


    public int capacity() {
        return items.length;
    }

    @Override
    public E dequeue() {
        if (front == rear) {
            throw new IllegalStateException("Queue empty");
        }
        return items[front++];
    }

    @Override
    public boolean enqueue(E e) {
        if (isFull()) {
            throw new IllegalStateException("Queue empty");
        }
        // 队尾没有空间了,需要执行数据迁移
        if (rear == capacity()) {
            // 数据迁移
            if (rear - front >= 0)  {
                System.arraycopy(items, front, items, 0, rear - front);
            }
            // 调整 front 与 rear
            rear -= front;
            front = 0;
        }
        items[rear++] = e;
        return true;
    }

    @Override
    public boolean isFull() {
        return rear == capacity() && front == 0;
    }

    @Override
    public boolean isEmpty() {
        return front == rear;
    }
}

链式队列

我们可以通过之前学习过的链表来实现队列，具体详见单向链表篇。其实主要就是利用了 出队就是链表头删除数据，入队就是尾节点添加数据

public class LinkedQueue<E> extends AbstractQueue<E> implements Queue<E> {

    private final SingleLinkedList<E> linkedList;

    public LinkedQueue() {
        this.linkedList = new SingleLinkedList<>();
    }

    @Override
    public E dequeue() {
        if (linkedList.isEmpty()) {
            throw new IllegalStateException("Queue empty");
        }
        return linkedList.remove();
    }

    @Override
    public boolean enqueue(E e) {
        return linkedList.add(e);
    }

    @Override
    public boolean isFull() {
        return false;
    }

    @Override
    public boolean isEmpty() {
        return linkedList.isEmpty();
    }
}

循环队列

刚刚的例子，当 rear == capacity 的时候，会出现数据迁移操作，这样性能受到影响，那如何避免呢？

原本数组是有头有尾的，是一条直线。现在我们把首尾相连，扳成了一个环。

环形队列

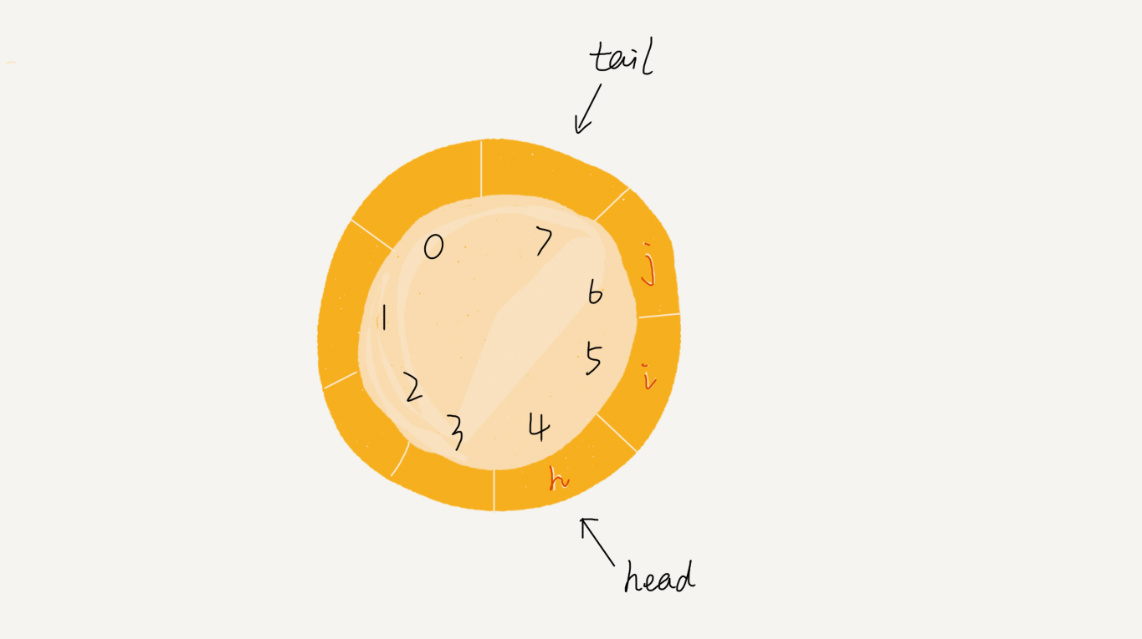
我们可以看到，图中这个队列的大小为 8，当前 head=4，tail=7。当有一个新的元素 a 入队时，我们放入下标为 7 的位置。但这个时候，我们并不把 tail 更新为 8，而是将其在环中后移一位，到下标为 0 的位置。当再有一个元素 b 入队时，我们将 b 放入下标为 0 的位置，然后 tail 加 1 更新为 1。所以，在 a，b 依次入队之后，循环队列中的元素就变成了下面的样子：

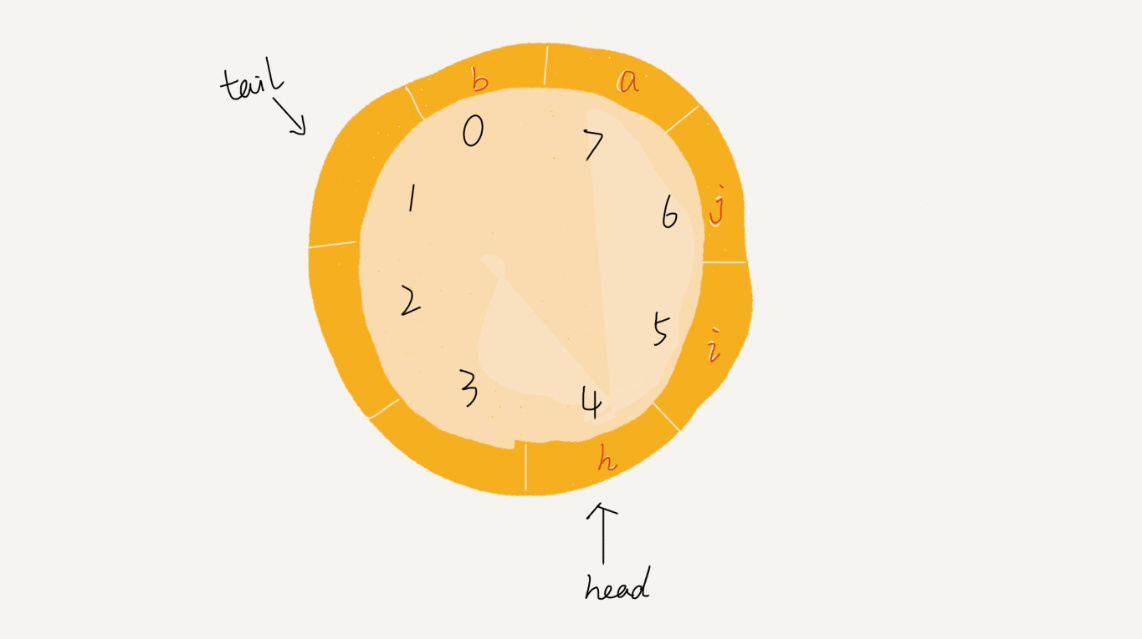
队列为空的判断依然是 front == rear，队列满的条件则是 (rear + 1) % capacity = front

你有没有发现，当队列满时，图中的 tail 指向的位置实际上是没有存储数据的。所以，循环队列会浪费一个数组的存储空间。

/**
 * 数组实现环形队列
 *
 * @param <E>
 */
public class ArrayCircleQueue<E> extends AbstractQueue<E> {

    /**
     * The queued items
     */
    final E[] items;
    /**
     * 队头指针
     */
    private int front;

    /**
     * 队尾指针
     */
    private int rear;

    public int capacity() {
        return items.length;
    }

    /**
     * Creates an ArrayQueue with the given capacity
     *
     * @param capacity the capacity of this queue
     */
    public ArrayCircleQueue(Class<E> type, int capacity) {
        if (capacity <= 0) {
            throw new IllegalArgumentException();
        }
        this.items = (E[]) Array.newInstance(type, capacity);
    }

    @Override
    public E dequeue() {
        if (front == rear) {
            throw new IllegalStateException("Queue empty");
        }
        E item = items[front];
        front = (front + 1) % items.length;
        return item;
    }

    @Override
    public boolean enqueue(E e) {
        checkNotNull(e);
        int newRear = (rear + 1) % items.length;
        if (newRear == front) {
            throw new IllegalStateException("Queue full");
        }
        items[rear] = e;
        this.rear = newRear;
        return true;
    }

    @Override
    public boolean isFull() {
        return (rear + 1) % items.length == front;
    }

    @Override
    public boolean isEmpty() {
        return rear == front;
    }
}

MageByte

Rang