离散对数(持续更新中)
1,DH&DLP
题目源码:
from Crypto.Util.number import *
import hashlib
class D_H():
def __init__(self):
self.a = getPrime(128)
self.b = getPrime(128)
self.p = getPrime(1024)
self.g = getPrime(128)
print("p =", oct(self.p))
print('g =', oct(self.g))
def Alice(self):
A = pow(self.g, self.a, self.p)
print('A =', oct(A))
def Bob(self):
B = pow(self.g, self.b, self.p)
print('B =', oct(B))
def key_exchange(self):
key = pow(self.g, self.a * self.b, self.p)
return key
DH = D_H()
DH.Alice()
DH.Bob()
key = DH.key_exchange()
flag = "flag{" + hashlib.md5(str(key).encode()).hexdigest() + "}"
"""
p = 0o100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000002320461720107654672567257101774542402073
g = 0o2065141432751712040220440246142105771015421
A = 0o43613040531475331260645277703363154024375552447624145423154467212453566671627031247565752140361214442354760036367561323225723114644705564775357161722423055427767542147531265612413043244400626062610066133355056455656354327315127131604056020315605217552254443755433425633455524145337447120342451441170743174123742307207301542043164563340422677
B = 0o60346662663461540211665020605034076206107430140346645020415164214412402345454104341770532135130621505726240703066624656170403450176106112505427262227076032102233051024443206700250621734407223434463067213634725130117240556410501066411312272344517322556714720077305705512606154144764640154454705523667767514601216365471777467432753500477011706
"""先分析源码,可知 求 key 即可得flag,求key 需先求 self.a ,self.b
而self.a , self.b 分别为A , B 的指数,所以涉及DLP (离散对数)
至此,目标清晰(self.a 默认为 a, self.b默认为 b)
继续:
这是道 密钥交换协议 (Diffie Hellman) 加 DLP 的 Pohlig-Hellman 算法 ,涉及p-1 光滑数
Diffie Hellman 原理较为简单,无需解释也可自行看懂
原理:

所以采用 中间人攻击 ,如图
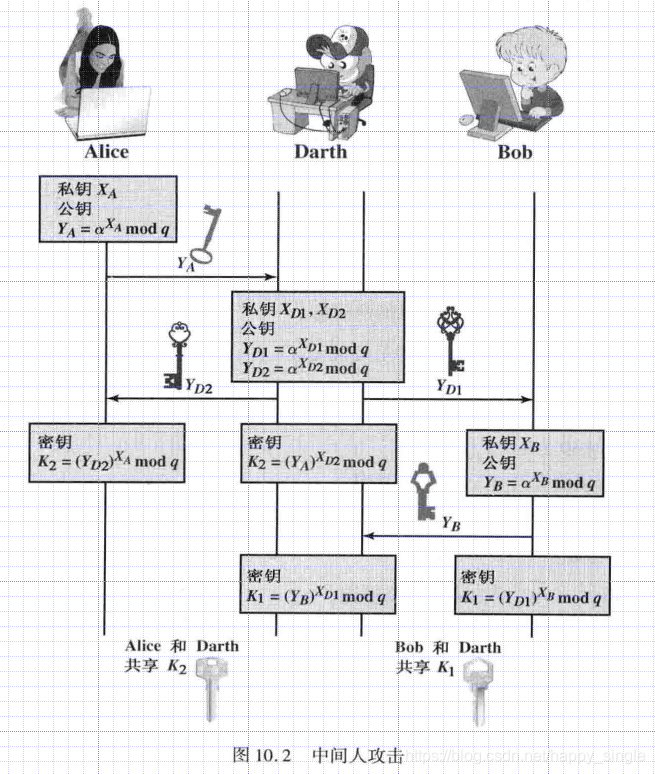
即 我们自行 生成两个私钥,X1,X2,用相同的a,q分别生成两个公钥,Y1,Y2,分别发给Alice ,Bob
由于我们 必然知道 自己的两个私钥,
$$K1=(Y1)^{XB} mod q=(YB)^{X1} mod q$$
X1,YB,q,Y1已知,据此通过离散对数求指数XB,即此题的 b ,同理可得 a
自行生成两个私钥 a1,b1,两个公钥,W1,W2
from Crypto.Util.number import *
import hashlib
class D_H():
def __init__(self):
self.a = getPrime(128) #私钥a
self.b = getPrime(128) #私钥b
self.p = 0o100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000002320461720107654672567257101774542402073
self.g = 0o2065141432751712040220440246142105771015421
print('a =',oct(self.a))
print('b =', oct(self.b))
def Alice(self):
A = pow(self.g, self.a, self.p)
print('W1 =', oct(A)) #Ya
def Bob(self):
B = pow(self.g, self.b, self.p)
print('W2 =', oct(B)) #Yb
def key_exchange(self):
key = pow(self.g, self.a * self.b, self.p)
return key
DH = D_H()
DH.Alice()
DH.Bob()
key = DH.key_exchange()
flag = "flag{" + hashlib.md5(str(key).encode()).hexdigest() + "}"
# # 中间人
# a1 = 0o2462471162741234772727054414536530023564165
# b1 = 0o3776362545773344220254412013272563345646375
# W1 = 0o30177410335615713542026512603323473205434005561747576441000340673116717446660223313444625136651624625241317244472674410576033351505145102532723042071050116471427334542406460562263224765334125507145737557104465406333501613713727135003611011143450112471232770123366033751722734673337036650302174034661504555667574715231200341006620333553077066
# W2 = 0o21767767521415454605102034111542047036764671756720324646106371712334761330532743112346114006302441445406533657740062602010422272601755373477507607505570626733347000552376671501627563674665230627166705564211645416753645310162172100735325175505371110602207023457024257032454332272025410051011476055743503274466610063274263742714643617465701710W1,W2,分别公布给两人,用以生成相应的K等式
K2 = pow(B,b1,p) # =pow(W2,b,p)
print(K2)
K1 = pow(A,a1,p) #=pow(W1,a,p)
print(K1)到此,a,b即在眼前
下面介绍一下离散对数中的 Pohig-Hellman算法
函数实现: base^e = a
discrete_log(a,base,ord,operation)如上,base为底,求a的对数
ord为base的阶,可以缺省,operation可以是'+'与'*',默认为'*'
通用的求离散对数的方法(Pohlig-Hellman+BSGS)
Pohig-Hellman算法是一种求解光滑阶循环群上的离散对数的方法。
-
要求a≡g^x (mod p)中 g必须是原根 (对于 g 不是原根的情况,需要利用原根将原方程转化成两个关于原根的离散对数问题。
-
要求阶是光滑的(p-1可拆为多个素数相乘)
光滑的,即形如此
(可将p改为十进制,有利理解)

从此中,便可知此题为何会用 离散对数中的 Pohig-Hellman算法
算法原理:
可先浅了解一下 阶,原根,时间复杂度


即 g^a ≡ 1 (mod p) ,当a为p-1时,g为模p的原根
时间复杂度:(不知其定义如何描述,可自行了解)
时间复杂度越来越大,执行的效率越来越低
若太复杂,计算时间所需太长,会崩,如下见

回归正题
$$g^x\equiv h(mod\ p)$$
$$1,φ(p)=p-1=p1^{k1}*p2^{k2}...pm^{km}(m为质因数个数)$$
2,对每个素因子pi,将x表示成pi进制,有
$$x = a0+a1pi+a2(pi)^2+a3(pi)^2+...+(a(ki-1))pi^{ki-1} (mod\ {p}_{i}^{ki})$$
(即把x写成pi进制,每个系数ai都小于pi)
3,对于$$g^x\equiv h(mod\ p)$$,两边同时乘以 $$\frac{p-1}{pi^r}$$
即 $$(a^x)^{\frac{p-1}{{p}_{i}^r}}\equiv b^{\frac{p-1}{{p}_{i}^r}} (mod\ p)$$
4,展开x,得到
$$(a^{{{p}_{i}^0+{p}_{i}^1a1+{p}_{i}^2a2...+{p}_{i}^{{k}_{i-1}{a}_{ki-1}}}})^\frac{p-1}{{p}_{i}^r}\equiv b^\frac{p-1}{{p}_{i}^r}(mod\ p)$$
5,当r=1时,展开,得
$$a^{a0*\frac{p-1}{pi}}*a^{(p-1)a1}*(a^{p-1})^{pa2}*(a^{p-1})^{p^2a3}...(a^{p-1})^{p^{{k}_{i}-2}a{k}_{i-1}}\equiv b^\frac{p-1}{{p}_{i}^r} (mod\ p)$$
6,观察知,第二项及此后的每一项,由欧拉定理$$a^{p-1}\equiv1 (mod\ p)$$ 得,每一项皆为1,故得(r=1)
$$a^{a0*\frac{p-1}{pi}}\equiv b^{\frac{p-1}{{p}_{i}^r}} (mod\ p)$$ => $$a0*\frac{p-1}{pi} \equiv \frac{p-1}{pi}(mod\ p-1)$$
因为ai∈[0,pi-1](前文提到了pi进制,我也不知所以然),故可以在复杂度$$O(pi)$$的时间内暴力求出a0
注:若$$a^j\equiv a^i (mod p)$$,则$$i\equiv j(mod\ p-1)$$
7,得到a0后,令r = r+1,回到步骤5,直到所有ai被求出后,可得到
$$x={p}_{i}^0a0+{p}_{i}^1a1+{p}_{i}^2a2...+{p}_{i}^{{k}_{i-1}}a{k}_{i-1}(mod\ {p}_{i}^{ki})$$
8,在算出m个关于x的式子后,即用中国剩余定理求解
值得一提到是,中国剩余定理所需n的组数需满足=> $$m^e<{n}_{1}*{n}_{2}*{n}_{3}...$$
所以无需所有p-1的质因子


可结合下面脚本理解(具体这就不加解释,公式打累了(手动狗头))
# K2 = 54814846335780447316835818815553396107825604069271218449213491151351336059792767162361300914069004913012467841792862632782405340663569408429208004574228303423550868433039264867808382293167572116274903923603187366829575727502616919165542138514088692003615212224589562650802481642791540343802658343564140775050
# p = int(0o100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000002320461720107654672567257101774542402073)
# W2 = int(0o21767767521415454605102034111542047036764671756720324646106371712334761330532743112346114006302441445406533657740062602010422272601755373477507607505570626733347000552376671501627563674665230627166705564211645416753645310162172100735325175505371110602207023457024257032454332272025410051011476055743503274466610063274263742714643617465701710)
import hashlib
"""
n = 89884656743115795386465259539451236680898848947115328636715040578866337902750481566354238661203768010560056939935696678829394884407208311246423715319737062188883946712432742638151109800623047059726541476042502884419075341171231440736956555270413618581675255342293149119974022969989259739901207135911877936187
factor(n-1)
# 2 * 659 * 144811523 * 158091863 * 167642023 * 194814973 * 198114301509256817 * 1524198318315919100927 * 302061228405984819868188635839278249994068296319393442016901959084878254985929326557136330675603997640265462782948042782543029960066166632904951616712643712462381886167331227465971149482608610738439655060064241698902750467248492676743
"""
# c = pow(m, secret, n)
# h = g^x mod p
def r(h, g, N, p, qi):
Zp = Zmod(p)
h = pow(h, N//qi, p)
g = pow(g, N//qi, p)
ri = discrete_log(Zp(h), Zp(g))
return int(ri)
m = 0o21767767521415454605102034111542047036764671756720324646106371712334761330532743112346114006302441445406533657740062602010422272601755373477507607505570626733347000552376671501627563674665230627166705564211645416753645310162172100735325175505371110602207023457024257032454332272025410051011476055743503274466610063274263742714643617465701710
n = 89884656743115795386465259539451236680898848947115328636715040578866337902750481566354238661203768010560056939935696678829394884407208311246423715319737062188883946712432742638151109800623047059726541476042502884419075341171231440736956555270413618581675255342293149119974022969989259739901207135911877936187
c = 54814846335780447316835818815553396107825604069271218449213491151351336059792767162361300914069004913012467841792862632782405340663569408429208004574228303423550868433039264867808382293167572116274903923603187366829575727502616919165542138514088692003615212224589562650802481642791540343802658343564140775050
tmp_list = [659, 144811523, 158091863, 167642023, 194814973]
r_list = []
for qi in tmp_list:
tmp = r(c,m,n-1,n,qi)
print(tmp)
r_list.append(tmp)
x = crt(r_list, tmp_list)
module = 1
for i in tmp_list:
module *= i
while True:
if int(x).bit_length()>128:
print('fail')
break
if int(pow(m, x, n))==c:
print('x =', x)
# flag = "flag{"+hashlib.md5(str(x).encode()).hexdigest()+"}"
# print(flag)
break
x += module回到题目,此处的x即为所求b,同理得a
最后
a = 288439857354393866763185538169340562833
b = 253100920167170926044570003097335817769
p = 89884656743115795386465259539451236680898848947115328636715040578866337902750481566354238661203768010560056939935696678829394884407208311246423715319737062188883946712432742638151109800623047059726541476042502884419075341171231440736956555270413618581675255342293149119974022969989259739901207135911877936187
g = 0o2065141432751712040220440246142105771015421
key = pow(g, a * b, p)
flag = "flag{" + hashlib.md5(str(key).encode()).hexdigest() + "}"
print(flag)
# flag{1515950b17d8b66efc6e47f812448721}至此,答题结束
闲聊:
2023 DASCTF - 0x401的ezDHKE,题型与此雷同,本以为能解,却棋差一招,对于光滑数的原根理解不够透彻

只随便传了个光滑数,便以为可解,实乃与此题无缘(bushi)
from Crypto.Util.number import *
from random import choice
def myPrime(bits):
while True:
n = 2
while n.bit_length() < bits:
n *= choice(sieve_base)
if isPrime(n + 1):
return n + 1
# g = 2
p = myPrime(1024)具体可见如下博客
博客链接参考:
密钥交换协议 (Diffie Hellman),Pohig-Hellman算法:
离散对数(La佬)
离散对数函数参数说明:

 浙公网安备 33010602011771号
浙公网安备 33010602011771号