NSSCTF 2nd Crypto复现

1，EzRSA

题目代码：

from Crypto.Util.number import *
from secret import flag
m = bytes_to_long(flag)
assert m.bit_length()<200
p = getPrime(512)
q = getPrime(512)
n = p*q
e = 3
c = pow(m, e, n)
kbits = 103
m = (m >> kbits) << kbits
Mod = getPrime(1024)
hint1 = (2021-2023*m) % Mod
hint2 = pow(2, 2023, Mod)
print('n =',n)
print('c =',c)
print('hint1 =',hint1)
print('hint2 =',hint2)
'''
n = 115383855234466224643769657979808398804254899116842846340552518876890834212233960206021018541117724144757264778086129841154749234706140951832603640953383528482125663673926452745186670807057426128028379664506531814550204605131476026038420737951652389070818761739123318769460392218629003518050621137961009397857
c = 5329266956476837379347536739209778690886367516092584944314921220156032648621405214333809779485753073093853063734538746101929825083615077
hint1 = 153580531261794088318480897414037573794615852052189508424770502825730438732573547598712417272036492121110446656514226232815820756435437665617271385368704576530324067841094570337328191161458300549179813432377043779779861066187597784486306748688798924645894867137996446960685210314180286437706545416961668988800
hint2 = 130939024886341321687705945538053996302793777331032277314813607352533647251650781154105954418698306293933779129141987945896277615656019480762879716136830059777341204876905094451068416223212748354774066124134473710638395595420261557771680485834288346221266495706392714094862310009374032975169649227238004805982
'''

 

简单点，就是 c 直接开 3 次方 ，即得 flag ：b'NSSCTF{Rea1_Si9n3n}'

 

 

但以学习的想法来写，以下为我的思考：

我想前半部分，他是参考 ctfshow 中 的一道题 Crypto-Comedy 来出题的，后半部分是m高位攻击

考点1： 在k倍的模下构造等式来求解

hint1 = (2021-2023*m) % Mod
hint2 = pow(2, 2023, Mod)

$$k*Mod = 2^{2023}-hint2$$

$$hint1 +2023*m-2021=0 ~mod ~Mod $$

再转化为$$hint1 +2023*m-2021=0 ~mod ~k*Mod$$

如此即可在 sagemath 里求解 m

考点2：m高位攻击

$$m^e\equiv c ~~ mod~n$$
$$(m_{high}+x)^e \equiv c ~~ mod~n$$
$$转换成多项式，即为~~f=(m_{high}+x)^e-c$$

n = 
c = 
e =
high_m = 
PR.<x> = PolynomialRing(Zmod(n))
f = (high_m + x)^e - c
x0 = f.small_roots(X=2^kbits, beta=1)[0]
m = int(high_m+x0)
print(long_to_bytes(m))

 exp:

from Crypto.Util.number import *
from gmpy2 import *
n = 115383855234466224643769657979808398804254899116842846340552518876890834212233960206021018541117724144757264778086129841154749234706140951832603640953383528482125663673926452745186670807057426128028379664506531814550204605131476026038420737951652389070818761739123318769460392218629003518050621137961009397857
c = 5329266956476837379347536739209778690886367516092584944314921220156032648621405214333809779485753073093853063734538746101929825083615077
hint1 = 153580531261794088318480897414037573794615852052189508424770502825730438732573547598712417272036492121110446656514226232815820756435437665617271385368704576530324067841094570337328191161458300549179813432377043779779861066187597784486306748688798924645894867137996446960685210314180286437706545416961668988800
hint2 = 130939024886341321687705945538053996302793777331032277314813607352533647251650781154105954418698306293933779129141987945896277615656019480762879716136830059777341204876905094451068416223212748354774066124134473710638395595420261557771680485834288346221266495706392714094862310009374032975169649227238004805982

e = 3
km = pow(2,2023)-hint2
PR.<m> = PolynomialRing(Zmod(km))
f = hint1+2023*m-2021
f = f.monic()
x = f.small_roots(X=2^200, beta=0.4)
print(x)
high_m=1746716778150027565782467891299010283212636160
kbits = 103
PR.<x> = PolynomialRing(Zmod(n))
f = (high_m + x)^e - c
x0 = f.small_roots(X=2^kbits, beta=1)[0]
m = int(high_m+x0)
print(long_to_bytes(m))
# b'NSSCTF{Rea1_Si9n3n}'

 

 

2,FunnyEncrypt

✧✡✭
✡✮ ✣✴✯ ✤✶✬✬✱ ✬✤ ✱✦✢✥✮✯✧✧, ✴✬✷✯ ✡✧ ✣✴✯ ✶✡✰✴✣. ✡✣ ❂✢✡✮✰✧ ✩✬✸✤✬✢✣, ✤✦✡✣✴, ✦✮✱ ✩✬✮✤✡✱✯✮✩✯. ✡✣ ✰✡✲✯✧ ✳✧ ✰✳✡✱✦✮✩✯ ★✴✯✮ ★✯ ✦✢✯ ✶✬✧✣, ✦✮✱ ✰✡✲✯✧ ✧✳✷✷✬✢✣ ★✴✯✮ ★✯ ✦✢✯ ✦✤✢✦✡✱. ✦✮✱ ✣✴✯ ✸✬✸✯✮✣ ★✯ ✰✡✲✯ ✳✷ ✴✬✷✯, ★✯ ✰✡✲✯ ✳✷ ✬✳✢ ✶✡✲✯✧. ✣✴✯ ★✬✢✶✱ ★✯ ✶✡✲✯ ✡✮ ✡✧ ✱✡✧✡✮✣✯✰✢✦✣✡✮✰ ✡✮✣✬ ✦ ✷✶✦✩✯ ✬✤ ✸✦✶✡✩✯ ✦✮✱ ✴✦✣✢✯✱, ★✴✯✢✯ ★✯ ✮✯✯✱ ✴✬✷✯ ✦✮✱ ✤✡✮✱ ✡✣ ✴✦✢✱✯✢. ✡✮ ✣✴✡✧ ★✬✢✶✱ ✬✤ ✤✯✦✢, ✴✬✷✯ ✣✬ ✤✡✮✱ ❂✯✣✣✯✢, ❂✳✣ ✯✦✧✡✯✢ ✧✦✡✱ ✣✴✦✮ ✱✬✮✯, ✣✴✯ ✸✬✢✯ ✸✯✦✮✡✮✰✤✳✶ ✶✡✤✯ ✬✤ ✤✦✡✣✴ ★✡✶✶ ✸✦✥✯ ✶✡✤✯ ✸✯✦✮✡✮✰✤✳✶.
✧✬✸✯✣✡✸✯✧ ★✯ ✣✴✡✮✥ ✬✤ ✱✢✯✦✸✧ ✦✧ ✤✦✮✣✦✧✡✯✧ - ✡✣'✧ ✯✦✧✵ ✣✬ ✱✬ ★✴✯✮ ✵✬✳ ✴✦✲✯ ✸✬✮✯✵, ✢✯✮✣, ✦✮✱ ★✬✢✥. ❂✳✣ ✵✬✳ ✩✦✮'✣ ✷✢✯✷✦✢✯ ✵✬✳✢✧✯✶✤ ✦✮✱ ✫✳✸✷ ✬✤✤ ✣✴✯ ✩✶✡✤✤: ✵✬✳ ✧✴✬✳✶✱ ✰✢✬★ ✵✬✳✢ ★✡✮✰✧ ✤✡✢✧✣. ✦ ✶✡✣✣✶✯ ❂✡✣ ✣✬★✦✢✱ ✣✴✯ ✱✢✯✦✸. ✧✣✯✷ ❂✵ ✧✣✯✷. ✣✦✥✯ ✦ ✧✣✯✷ ✤✬✢★✦✢✱. ✦✤✣✯✢ ✦✶✶, ✡✣'✧ ✵✬✳✢ ✸✡✧✧✡✬✮.
✥✯✯✷ ✤✦✡✣✴ ✦✮✱ ✴✬✷✯ ✤✬✢ ✣✴✯ ✤✳✣✳✢✯. ✸✦✥✯ ✵✬✳✢ ✸✬✧✣ ✧✡✮✩✯✢✯ ✱✢✯✦✸✧, ✦✮✱ ★✴✯✮ ✣✴✯ ✬✷✷✬✢✣✳✮✡✣✡✯✧ ✩✬✸✯, ✣✴✯✵ ★✡✶✶ ✤✡✰✴✣ ✤✬✢ ✣✴✯✸. ✡✣ ✸✦✵ ✣✦✥✯ ✦ ✧✯✦✧✬✮ ✬✢ ✸✬✢✯, ❂✳✣ ✣✴✯ ✯✮✱✡✮✰ ★✡✶✶ ✮✬✣ ✩✴✦✮✰✯. ✦✸❂✡✣✡✬✮, ❂✯✧✣, ❂✯✩✬✸✯ ✦ ✢✯✦✶✡✣✵. ✦✮ ✳✮✩✯✢✣✦✡✮ ✤✳✣✳✢✯, ✬✮✶✵ ✬✮✯ ✧✣✯✷ ✦✣ ✦ ✣✡✸✯, ✣✴✯ ✴✬✷✯ ✩✦✮ ✢✯✦✶✡✪✯ ✣✴✯ ✱✢✯✦✸ ✬✤ ✣✴✯ ✴✡✰✴✯✧✣. ★✯ ✸✳✧✣ ✣✢✯✦✧✳✢✯ ✣✴✯ ✱✢✯✦✸, ✣✬ ✷✢✬✣✯✩✣ ✡✣ ✦ ✧✯✦✧✬✮, ✶✯✣ ✡✣ ✡✮ ✣✴✯ ✴✯✦✢✣ ❋✳✡✯✣✶✵ ✰✯✢✸✡✮✦✶.
✬✮✶✵ ★✴✯✮ ✵✬✳ ✳✮✱✯✢✧✣✦✮✱ ✣✴✯ ✣✢✳✯ ✸✯✦✮✡✮✰ ✬✤ ✶✡✤✯ ✩✦✮ ✵✬✳ ✶✡✲✯ ✣✢✳✶✵. ❂✡✣✣✯✢✧★✯✯✣ ✦✧ ✶✡✤✯ ✡✧, ✡✣'✧ ✧✣✡✶✶ ★✬✮✱✯✢✤✳✶, ✦✮✱ ✡✣'✧ ✤✦✧✩✡✮✦✣✡✮✰ ✯✲✯✮ ✡✮ ✣✢✦✰✯✱✵. ✡✤ ✵✬✳'✢✯ ✫✳✧✣ ✦✶✡✲✯, ✣✢✵ ✴✦✢✱✯✢ ✦✮✱ ✣✢✵ ✣✬ ✶✡✲✯ ★✬✮✱✯✢✤✳✶✶✵.
✡ ❂✯✶✡✯✲✯ ✣✴✯✢✯ ✡✧ ✦ ✷✯✢✧✬✮ ★✴✬ ❂✢✡✮✰✧ ✧✳✮✧✴✡✮✯ ✡✮✣✬ ✵✬✳✢ ✶✡✤✯. ✣✴✦✣ ✷✯✢✧✬✮ ✸✦✵ ✴✦✲✯ ✯✮✬✳✰✴ ✣✬ ✧✷✢✯✦✱ ✦✢✬✳✮✱. ❂✳✣ ✡✤ ✵✬✳ ✢✯✦✶✶✵ ✴✦✲✯ ✣✬ ★✦✡✣ ✤✬✢ ✧✬✸✯✬✮✯ ✣✬ ❂✢✡✮✰ ✵✬✳ ✣✴✯ ✧✳✮ ✦✮✱ ✰✡✲✯ ✵✬✳ ✦ ✰✬✬✱ ✤✯✯✶✡✮✰, ✣✴✯✮ ✵✬✳ ✸✦✵ ✴✦✲✯ ✣✬ ★✦✡✣ ✦ ✶✬✮✰ ✣✡✸✯.
✡✮ ✦ ★✬✢✱,✡ ✴✬✷✯ ✵✬✳ ★✡✶✶ ✶✡✥✯ ✩✢✵✷✣✬✰✢✦✷✴✵.✣✴✡✧ ✡✧ ✵✬✳✢ ✤✶✦✰:✮✧✧✩✣✤{✩✢✵✷✣✬_✡✧_✧✬_✡✮✣✯✢✯✧✣✡✮✰_★✴✵_✱✬✮'✣_✵✬✳_✫✬✡✮_✳✧}

 起初我以为是类似古典密码之类的，在线解密就好，结果找不到，古典密码还是做少了，加油

出题人的想法是26个星星对应26个字母，将之转换为26个小写字母，再词频分析得flag

 首先如何知道是26个不同的星星： 字频统计

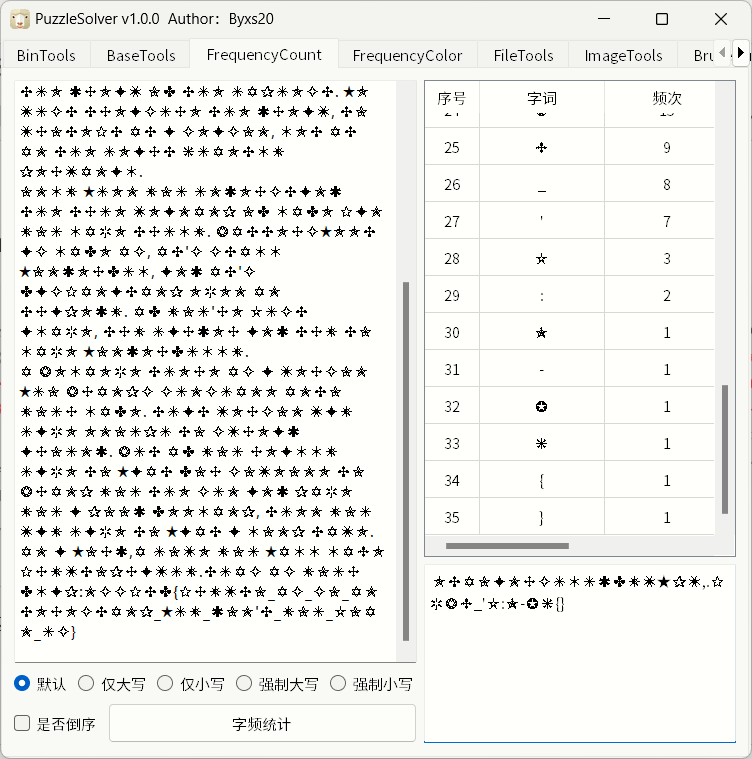
 再通过 cyberchef 的 substitute 替换

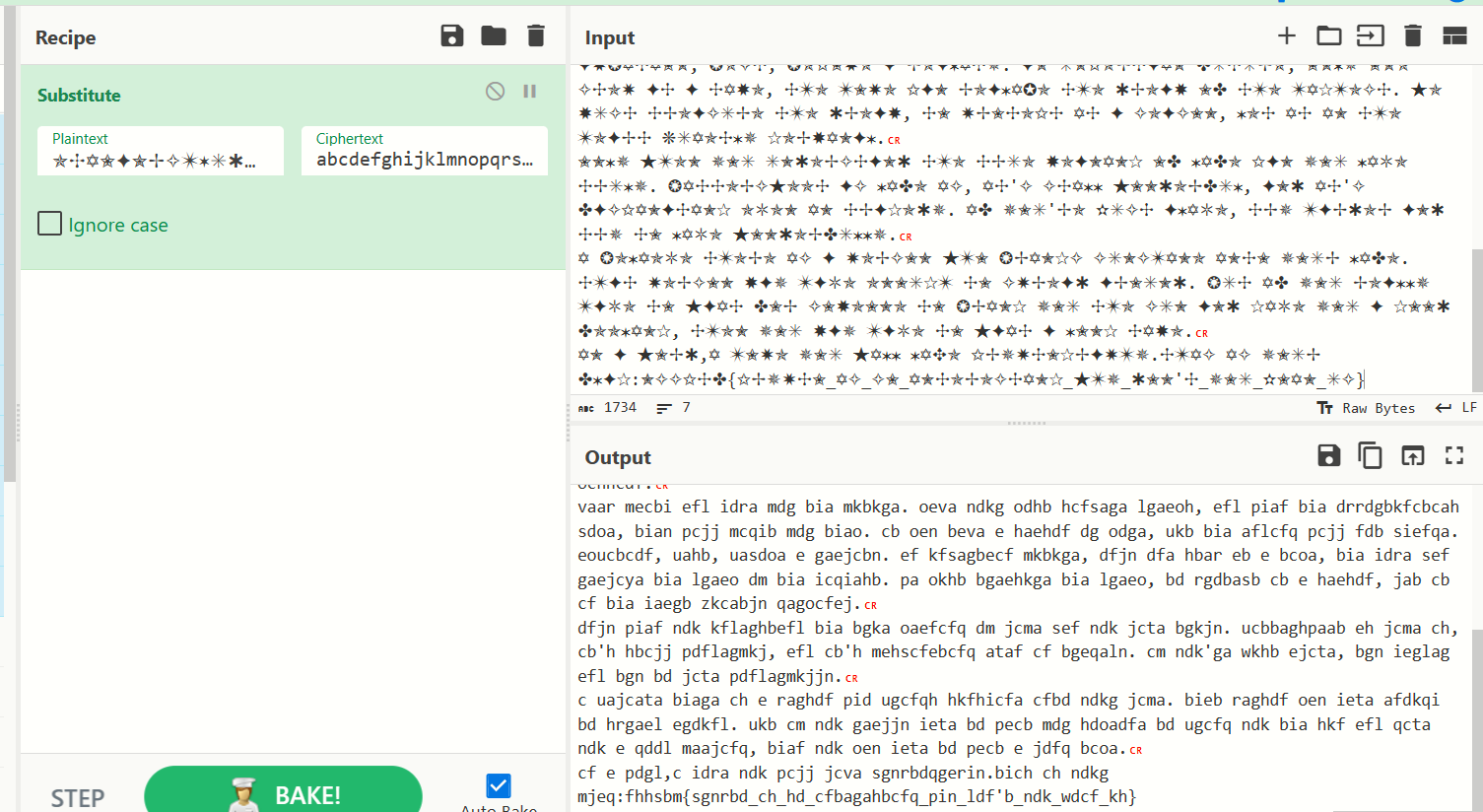
 最后词频分析即可   quipqiup - cryptoquip and cryptogram solver

也可以        Substitution Solver | guballa.de

 

3，Math

from secret import flag
from Crypto.Util.number import *
import gmpy2

length = len(flag)
flag1 = flag[:length//2]
flag2 = flag[length//2:]
e = 65537

m1 = bytes_to_long(flag1)
p = getPrime(512)
q = getPrime(512)
n = p*q
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)

p1 = gmpy2.invert(p,q)
q1 = gmpy2.invert(q,p)
c = pow(m1,e,n)

print("p1=",p1)
print("q1=",q1)
print("c=",c)
print("phi=",phi)
# 24
"""
p1= 3020925936342826638134751865559091272992166887636010673949262570355319420768006254977586056820075450411872960532347149926398408063119965574618417289548987
q1= 4671408431692232396906683283409818749720996872112784059065890300436550189441120696235427299344866325968178729053396743472242000658751114391777274910146291
c= 25112054943247897935419483097872905208058812866572413543619256987820739973912338143408907736140292730221716259826494247791605665059462509978370784276523708331832947651238752021415405546380682507724076832547566130498713598421615793975775973104012856974241202142929158494480919115138145558312814378701754511483
phi= 57503658815924732796927268512359220093654065782651166474086873213897562591669139461637657743218269483127368502067086834142943722633173824328770582751298229218384634668803018140064093913557812104300156596305487698041934061627496715082394633864043543838906900101637618600513874001567624343801197495058260716932
"""

m2 = bytes_to_long(flag2)
p = getPrime(1024)
q = getPrime(1024)
n = p * q
c = pow(m2, e, n)
hint = pow(2023 * p + 114514, q, n)
print("n=",n)
print("c=",c)
print("hint=",hint)
# 27
"""
n= 12775720506835890504634034278254395430943267336816473660983646973423280986156683988190224391394224069040565587173690009193979401332176772774003070053150665425296356891182224095151626957780349726980433545162004592720236315207871365869074491602494662741551613634958123374477023452496165047922053316939727488269523121920612595228860205356006298829652664878874947173274376497334009997867175453728857230796230189708744624237537460795795419731996104364946593492505600336294206922224497794285687308908233911851722675754289376914626682400586422368439122244417279745706732355332295177737063024381192630487607768783465981451061
c= 11915755246503584850391275332434803210208427722294114071001100308626307947436200730224125480063437044802693983505018296915205479746420176594816835977233647903359581826758195341201097246092133133080060014734506394659931221663322724002898147351352947871411658624516142945817233952310735792476179959957816923241946083918670905682025431311942375276709386415064702578261223172000098847340935816693603778431506315238612938066215726795441606532661443096921685386088202968978123769780506210313106183173960388498229061590976260661410212374609180449458118176113016257713595435899800372393071369403114116302366178240855961673903
hint= 3780943720055765163478806027243965253559007912583544143299490993337790800685861348603846579733509246734554644847248999634328337059584874553568080801619380770056010428956589779410205977076728450941189508972291059502282197067064652703679207594494311426932070873126291964667101759741689303119878339091991064473009603015444698156763131697516348762529243379294719509271792197450290763350043267150173332933064667716343268081089911389405010661267902446894363575630871542572200564687271311946580866369204751787686029541644463829030926902617740142434884740791338666415524172057644794094577876577760376741447161098006698524808
"""

题目由两部分组成，第一部分是p、q的逆元，第二部分是通过gcd求p

在风大的rsa里有原题，这里找了一份，放在后面

第一部分：

p1 = gmpy2.invert(p,q)
q1 = gmpy2.invert(q,p)

$$pp_1 = 1+k_1q$$

$$qq_1=1+k_2p$$

$$两式相乘，得:np_1q_1 = 1+k_2p+k_2q+k_1k_2n$$

$$=>(p_1q_1-k_1k_2)n = pp_1+qq_1-1$$

p1为510位，q1为511位，p、q都为512位，n就为1024位(这里求出后看了眼是1023位)，所以pp_1+qq_1-1为1023位，设(p_1q_1-k_1k_2)n 为k，可推断出k<2，即k=1（？？？）

（不理解k为1，也可直接爆破k）

又$$\varphi(n)=(p-1)*(q-1)$$ ,联立解二元一次方程求出p，q

$$\begin{cases}
 pq = pp_1+qq_1-1\\
 \varphi(n)=(p-1)*(q-1)
\end{cases}$$

import libnum
import sympy
p1= 
q1= 
c= 
phi= 
e = 
p, q = sympy.symbols('p q')
for k in range(1,10):
    m1 = sympy.solve([p*p1+q*q1-1-k*p*q,(p-1)*(q-1)-phi],[p,q])
    p = m1[0][0]
    q = m1[0][1]
    n=p*q
    d = libnum.invmod(e,phi)
    m1 = libnum.n2s(pow(c,d,int(n)))
    print(m1)
    break

 第二部分：

hint = pow(2023 * p + 114514, q, n)
# n 已知

$$ hint = (2023p+114514)^q ~mod~n$$

=>

$$hint+k_1n=(2023p+114514)^q   ~~~~~~~~~~~两边同时mod~p$$

$$=>hint = 114514^q ~mod~p$$

$$再由费马小定理,a^p\equiv a~(mod~p)，把 ~114514^q看成一个整体，得$$

$$hint = (114514^q)^p ~mod~p$$

$$kp = 114514^n-hint$$

 

p = gcd(kp,n)

exp:

import libnum
import sympy
p1= 3020925936342826638134751865559091272992166887636010673949262570355319420768006254977586056820075450411872960532347149926398408063119965574618417289548987
q1= 4671408431692232396906683283409818749720996872112784059065890300436550189441120696235427299344866325968178729053396743472242000658751114391777274910146291
c= 25112054943247897935419483097872905208058812866572413543619256987820739973912338143408907736140292730221716259826494247791605665059462509978370784276523708331832947651238752021415405546380682507724076832547566130498713598421615793975775973104012856974241202142929158494480919115138145558312814378701754511483
phi= 57503658815924732796927268512359220093654065782651166474086873213897562591669139461637657743218269483127368502067086834142943722633173824328770582751298229218384634668803018140064093913557812104300156596305487698041934061627496715082394633864043543838906900101637618600513874001567624343801197495058260716932
e = 65537
p,q = sympy.symbols('p q')
m1 = sympy.solve([p*p1+q*q1-1-p*q,(p-1)*(q-1)-phi],[p,q])
p = m1[0][0]
q = m1[0][1]
n=p*q
d = libnum.invmod(e,phi)
m1 = libnum.n2s(pow(c,d,int(n)))

n= 12775720506835890504634034278254395430943267336816473660983646973423280986156683988190224391394224069040565587173690009193979401332176772774003070053150665425296356891182224095151626957780349726980433545162004592720236315207871365869074491602494662741551613634958123374477023452496165047922053316939727488269523121920612595228860205356006298829652664878874947173274376497334009997867175453728857230796230189708744624237537460795795419731996104364946593492505600336294206922224497794285687308908233911851722675754289376914626682400586422368439122244417279745706732355332295177737063024381192630487607768783465981451061
c= 11915755246503584850391275332434803210208427722294114071001100308626307947436200730224125480063437044802693983505018296915205479746420176594816835977233647903359581826758195341201097246092133133080060014734506394659931221663322724002898147351352947871411658624516142945817233952310735792476179959957816923241946083918670905682025431311942375276709386415064702578261223172000098847340935816693603778431506315238612938066215726795441606532661443096921685386088202968978123769780506210313106183173960388498229061590976260661410212374609180449458118176113016257713595435899800372393071369403114116302366178240855961673903
hint= 3780943720055765163478806027243965253559007912583544143299490993337790800685861348603846579733509246734554644847248999634328337059584874553568080801619380770056010428956589779410205977076728450941189508972291059502282197067064652703679207594494311426932070873126291964667101759741689303119878339091991064473009603015444698156763131697516348762529243379294719509271792197450290763350043267150173332933064667716343268081089911389405010661267902446894363575630871542572200564687271311946580866369204751787686029541644463829030926902617740142434884740791338666415524172057644794094577876577760376741447161098006698524808
kp = pow(114514,n,n)-hint
p = libnum.gcd(kp,n)
q = n//p
phi = (p-1)*(q-1)
d = libnum.invmod(65537,phi)
m2 = libnum.n2s(pow(c,d,n))
print(m1+m2)

 

4,LatticeLCG

格，不会，根本还不会，以后学会再回来看看