如何理解拓扑排序算法(转)
对于一条有向边(u,v),定义u < v;满足所有这样条件的结点序列称为拓扑序列。拓扑排序就是求一个有向图的拓扑序列的算法。
一个有向图顶点的拓扑序列不是惟一的。并不是任何有向图的顶点都可以排成拓扑序列,有环图是不能排的。
例子:比如排课问题,比如士兵排队问题等。
拓扑排序在实际生活中和算法中都有很大的应用。比如要排一下几门课程的先后次序,我们可以把课程抽象成结点,把什么课是什么课的基础抽象成边,那么该图的一个拓扑序列就是这些课的一个可行的先后次序。各种语言的编译器都用到了拓扑排序。
数学基础:
什么是拓扑排序(Topological Sort)?简单地说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
回顾离散数学中关于偏序和全序的定义:
若集合X上的关系R是自反的、反对称的和传递的,则称只是集合X上的偏序关系。
设R是集合X上的偏序(Partial Order),如果对每个x,y∈X必有xRy或yRx,则称R是集合X上的全序关系。
直观地看,偏序指集合中仅有部分成员之间可比较,而全序指集合中全体成员之间均可比较。[例如],图7.25所示的两个有向图,图中弧(x,y)表示x≤y,则(a)表示偏序,(b)表示全序。若在(a)的有向图上人为地加一个表示v2≤v3的弧(符号“≤”表示v2领先于v3),则(a)表示的亦为全序,且这个全序称为拓扑有序(Topological Order),而由偏序定义得到拓扑有序的操作便是拓扑排序。
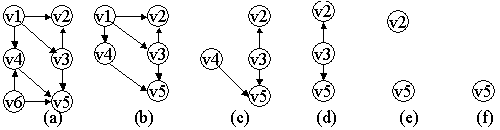
AOV-网及其拓扑有序序列产生的过程
(a)AOV-网;(b)输出v6之后;(c)输出v1之后;(d)输出v4之后;(e)输出v3之后;(f)输出v2之后
[思想]:
一、从有向图中选取一个没有前驱的顶点,并输出之;
二、从有向图中删去此顶点以及所有以它为尾的弧;
重复上述两步,直至图空,或者图不空但找不到无前驱的顶点为止。没有前驱 -- 入度为零,删除顶点及以它为尾的弧-- 弧头顶点的入度减1。
Status Topological Sort(ALGraph G){ //有向图G采用邻接表存储结构。 //若G无回路,则输出G的顶点的1个拓扑序列并返回OK,否则ERROR。 FindInDegree(G,indegree); //对各顶点求入度indegree[0..vernum-1] InitStack(S); for(i=0;i<G.vexnum; ++i) if(!indegree[i])Push(S,i) //建零入度顶点栈,s入度为0者进栈 count=0; //对输出顶点计数 while (!StackEmpty(S)) { Pop(S,i); printf(i,G.vertices[i].data); ++count; //输出i号顶点并计数 for(p=G.vertices[i].firstarc;p; p=p—>nextarc) { k=p—>adivex; //对i号顶点的每个邻接点的入度减1 if(!(--indegree[k]))Push(S,k);//若入度减为0,则入栈 }//for }//while if(count<G.vexnum) return ERROR; //该有向图有回路 else return OK; }//TopologicalSort
思想:
维护一个顶点入度为0的栈,
每次取栈顶元素top输出,对于top相邻的点进行入度数-1处理,处理后如果度数为0,再次入栈.
执行n次出栈操作,便可输出一个图的拓扑序.
判断是否包含有向环:如果入度为0的栈为空(top==-1),则说明包含有向环.(证明:无环时总有点入度为0).
时间复杂度:
1.搜索入度为0的顶点,建栈所需时间O(n);
2.无有向环时,每个顶点入栈一次,出栈一次,每条边扫描一次且仅一次,时间复杂度O(m).
3.总复杂度:O(n+m).
算法 ,总的时间复杂度为O(n+e)。
出处:http://shanyou.cnblogs.com/
版权:本文版权归作者和博客园共有
转载:欢迎转载,为了保存作者的创作热情,请按要求【转载】,谢谢
要求:未经作者同意,必须保留此段声明;必须在文章中给出原文连接;否则必究法律责任



