训练神经网络适合使用交叉熵错误率,而不是分类错误率或是均方差
一. 二次代价函数的不足
对于大多数人来说,犯错是一件让人很不开心的事情。但反过来想,犯错可以让我们意识到自己的不足,然后我们很快就学会下次不能再犯错了。犯的错越多,我们学习进步就越快。
同样的,在神经网络训练当中,当神经网络的输出与标签不一样时,也就是神经网络预测错了,这时我们希望神经网络可以很快地从错误当中学习,然后避免再预测错了。那么现实中,神经网络真的会很快地纠正错误吗?
我们来看一个简单的例子:
上图是一个只有一个神经元的模型。我们希望输入1的时候,模型会输出0(也就是说,我们只有一个样本(x=1, y=0))。假设我们随机初始化权重参数w=2.0,偏置参数b=2.0。激活函数为sigmoid函数。所以模型的第一次输出为:
以一个神经元的二类分类训练为例,进行两次实验(ANN常用的激活函数为sigmoid函数,该实验也采用该函数):输入一个相同的样本数据x=1.0(该样本对应的实际分类y=0);两次实验各自随机初始化参数,从而在各自的第一次前向传播后得到不同的输出值,形成不同的代价(误差):
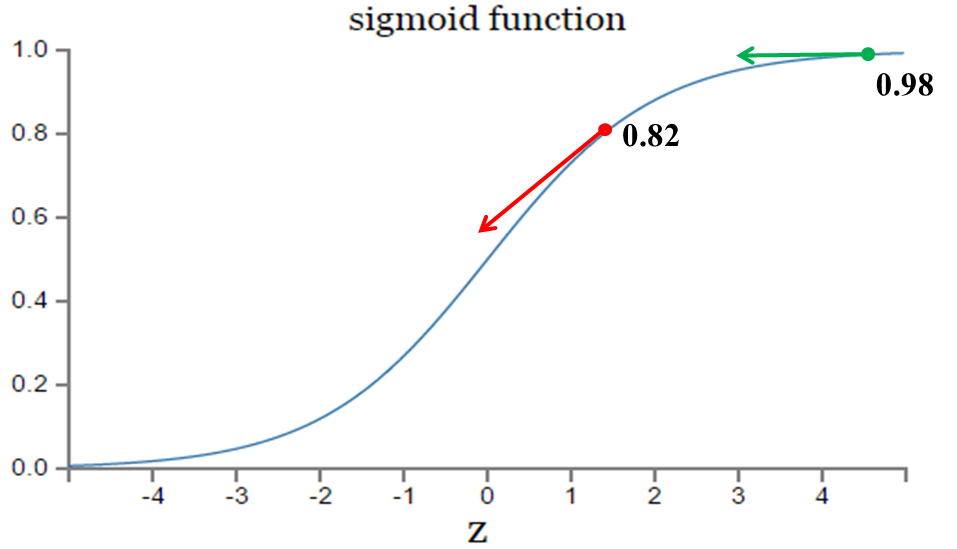
实验1:第一次输出值为0.82
实验2:第一次输出值为0.98
在实验1中,随机初始化参数,使得第一次输出值为0.82(该样本对应的实际值为0);经过300次迭代训练后,输出值由0.82降到0.09,逼近实际值。而在实验2中,第一次输出值为0.98,同样经过300迭代训练,输出值只降到了0.20。
从两次实验的代价曲线中可以看出:实验1的代价随着训练次数增加而快速降低,但实验2的代价在一开始下降得非常缓慢;直观上看,初始的误差越大,收敛得越缓慢。
其实,误差大导致训练缓慢的原因在于使用了二次代价函数。二次代价函数的公式如下:
其中,C表示代价,x表示样本,y表示实际值,a表示输出值,n表示样本的总数。为简单起见,同样一个样本为例进行说明,此时二次代价函数为:
目前训练ANN最有效的算法是反向传播算法。简而言之,训练ANN就是通过反向传播代价,以减少代价为导向,调整参数。参数主要有:神经元之间的连接权重w,以及每个神经元本身的偏置b。调参的方式是采用梯度下降算法(Gradient descent),沿着梯度方向调整参数大小。w和b的梯度推导如下:
其中,z表示神经元的输入,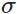
如图所示,实验2的初始输出值(0.98)对应的梯度明显小于实验1的输出值(0.82),因此实验2的参数梯度下降得比实验1慢。这就是初始的代价(误差)越大,导致训练越慢的原因。与我们的期望不符,即:不能像人一样,错误越大,改正的幅度越大,从而学习得越快。
可能有人会说,那就选择一个梯度不变化或变化不明显的激活函数不就解决问题了吗?图样图森破,那样虽然简单粗暴地解决了这个问题,但可能会引起其他更多更麻烦的问题。而且,类似sigmoid这样的函数(比如tanh函数)有很多优点,非常适合用来做激活函数,具体请自行google之。
二. 交叉熵代价函数
换个思路,我们不换激活函数,而是换掉二次代价函数,改用交叉熵代价函数:其中,x表示样本,n表示样本的总数。那么,重新计算参数w的梯度:
其中(具体证明见附录):
因此,w的梯度公式中原来的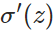

实际情况证明,交叉熵代价函数带来的训练效果往往比二次代价函数要好。
在使用神经网络做分类和预测的工作的时候,使用交叉熵模型来评估分类性能,往往要比分类错误率或是均方差模型更好。
实例
下面举个预测一个人属于哪个党派的例子。(来描述这个从的特征有很多,像年龄、性别、收入等。这里不讨论。)
将这个人的特征数据输入我们的分类模型,得到一组向量,来表示他/她属于哪个党派的概率。
模型一
| 预测结果 | 目标 | 正确吗? |
|---|---|---|
| 0.3 0.3 0.4 | 0 0 1 (democrat) | yes |
| 0.3 0.4 0.3 | 0 1 0 (republican) | yes |
| 0.1 0.2 0.7 | 1 0 0 (other) | no |
稍微解释一下,第一行0.3 0.3 0.4 | 0 0 1 (democrat) | yes的意思是:预测是other的概率是0.3;预测为republican的概率是0.3;预测是democrat的概率是0.4;而目标是democrat。
此时,
分类错误率:1/3 = 0.33
错误率
模型二
我们再看一个模型的分类结果。
| 预测结果 | 目标 | 正确吗? |
|---|---|---|
| 0.1 0.2 0.7 | 0 0 1 (democrat) | yes |
| 0.1 0.7 0.2 | 0 1 0 (republican) | yes |
| 0.3 0.4 0.3 | 1 0 0 (other) | no |
分类错误率:1/3 = 0.33
但是,我们可以观察到,前两项的分类结果有明显不同,所以直观上讲,第二个模型要比第一个模型更可靠。
交叉熵错误率模型的效果
仍然通过上面两个例子,我们看一下交叉熵的表现如何。(有关「熵」的计算,可以参考《统计学习方法》的5.2.2节)
模型一
计算第一行的熵,二、三行同理。-( (ln(0.3)*0) + (ln(0.3)*0) + (ln(0.4)*1) ) = -ln(0.4)然后得到平均交叉熵错误率(average cross-entropy error, ACE)
-(ln(0.4) + ln(0.4) + ln(0.1)) / 3 = 1.38第一行的均方差
(0.3 - 0)^2 + (0.3 - 0)^2 + (0.4 - 1)^2 = 0.09 + 0.09 + 0.36 = 0.54然后得到
(0.54 + 0.54 + 1.34) / 3 = 0.81- 模型二
ACE:-(ln(0.7) + ln(0.7) + ln(0.3)) / 3 = 0.64
均方差:(0.14 + 0.14 + 0.74) / 3 = 0.34
对比
| 项目 | 模型一 | 模型二 |
|---|---|---|
| ACE | 1.38 | 0.64 |
| 分类错误率 | 0.33 | 0.33 |
| 均方差 | 0.81 | 0.34 |
这样看起来ACE和均方差明显优于分类错误率,同时ACE和均方差相比差别不大。但是,考虑到均方差计算量要稍大于ACE。
总结
所以在应用上面三种方式评估结果的时候,要看你想做什么。
比如,你只想看在特定样本集上的结果的准确性,那就用分类错误率来评估。因为,此时你不需要知道得到每个结果的概率,这些对最终结果没有任何辅助说明意义。
但是,在训练分类模型,和长期评估的时候,ACE和均方差就会更远好一些。
交叉熵代价函数是如何产生的?
以偏置b的梯度计算为例,推导出交叉熵代价函数:
在第1小节中,由二次代价函数推导出来的b的梯度公式为:
为了消掉该公式中的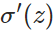
即:
对两侧求积分,可得:
而这就是前面介绍的交叉熵代价函数。
附录:
sigmoid函数为:
可证:
参考:



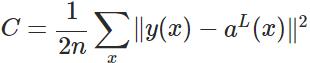
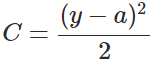
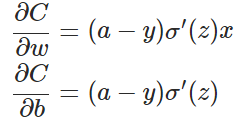
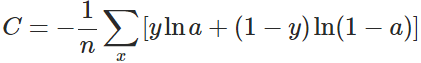
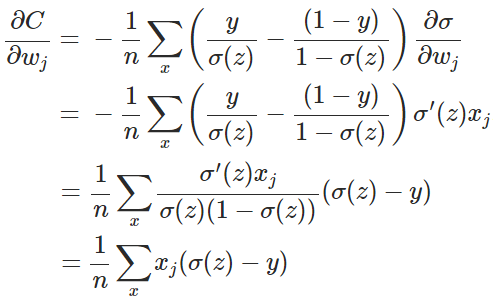
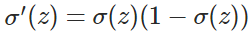
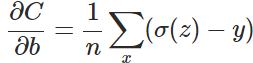
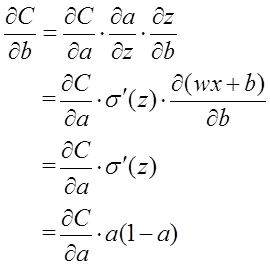
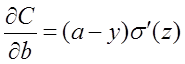
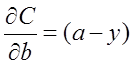
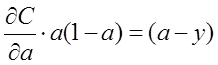
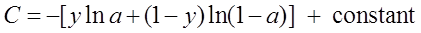

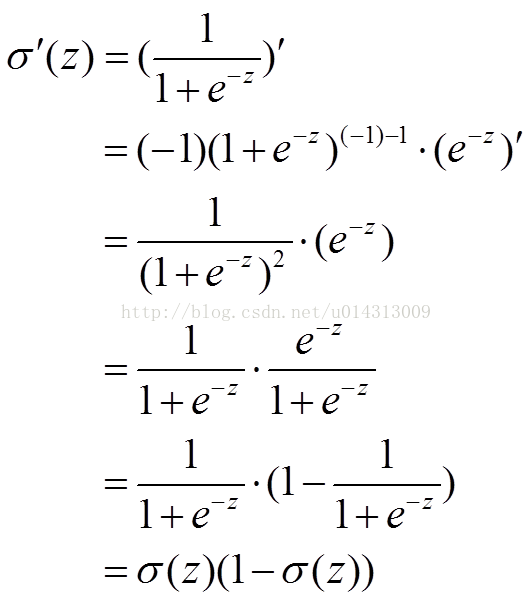

 浙公网安备 33010602011771号
浙公网安备 33010602011771号