[机器学习] 性能评估指标（精确率、召回率、ROC、AUC)

混淆矩阵

介绍这些概念之前先来介绍一个概念：混淆矩阵（confusion matrix）。对于 k 元分类，其实它就是一个k x k的表格，用来记录分类器的预测结果。对于常见的二元分类，它的混淆矩阵是 2x2 的。

假设要对 15 个人预测是否患病，使用 1 表示患病，使用 0 表示正常。预测结果如下：

预测值：	1	1	1	1	1	0	0	0	0	0	1	1	1	0	1
真实值：	0	1	1	0	1	1	0	0	1	0	1	0	1	0	0

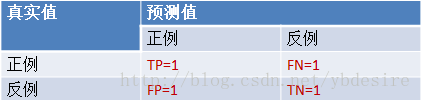
将上面的预测结果转为混淆矩阵，如下：

上图展示了一个二元分类的混淆矩阵，从该混淆矩阵可以得到以下信息：

• 样本数据总共有 5 + 2 + 4 + 4 = 15 个

• 真实值为 1 并且预测值也为 1 的样本有 5 个，真实值为 1 预测值为 0 的样本有 2 个，真实值为 0 预测值为 1 的样本有 4 个，真实值为 0 预测值也为 0 的样本有 4 个。

二元分类问题可以获得 True Positive（TP，真阳性）、False Positive（FP，假阳性）、 False Negative（FN，假阴性） 和 True Negative（TN，真阴性）。这四个值分别对应二元分类问题的混淆矩阵的四个位置。

小技巧：上面的这四个概念经常会被搞混淆（难道混淆矩阵的名称就是这么来的？），这里有个小方法帮你记住它。在医学上，一般认为阳性是患病，阴性是正常。所以只要出现“阳性”关键字就表示结果为患病，此外，阳性也分为真阳性和假阳性，从名称就可以看出：真阳性表示确确实实的阳性，也就是说实际为阳性（患病），预测也为阳性（患病）；假阳性表示不真实的阳性，也就是说实际为阴性（正常），预测为阳性（患病）。真阴性和假阴性也可以按照上面的方式来简单理解。

很明显，这里的 TP=5，FP=2，FN=4，TN=4。

1.准确率P、召回率R、F1 值

• 准确率（Precision）：P=TP/(TP+FP)。  通俗地讲，就是预测正确的正例数据占预测为正例数据的比例。
• 召回率（Recall）：    R=TP/(TP+FN)。  通俗地讲，就是预测为正例的数据占实际为正例数据的比例
• F1值（F score）：

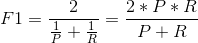
• 正如下图所示，F1的值同时受到P、R的影响，单纯地追求P、R的提升并没有太大作用。在实际业务工程中，结合正负样本比，的确是一件非常有挑战的事。
• 图像展示
  

什么是AUC

      根据维基百科的描述，AUC（Area under the Curve of ROC）是ROC曲线下方的面积，是判断二分类预测模型优劣的标准。ROC（receiver operating characteristic curve）接收者操作特征曲线，是由二战中的电子工程师和雷达工程师发明用来侦测战场上敌军载具（飞机、船舰）的指标，属于信号检测理论。ROC曲线的横坐标是伪阳性率（也叫假正类率，False Positive Rate），纵坐标是真阳性率（真正类率，True Positive Rate），相应的还有真阴性率（真负类率，True Negative Rate）和伪阴性率（假负类率，False Negative Rate）, AUC用于衡量“二分类问题”机器学习算法性能（泛化能力）。

我们知道，我们常用ACC准确率来判断分类器分类结果的好坏，既然有了ACC为什么还需要ROC呢，很重要的一个因素是实际的样本数据集中经常会出现数据偏斜的情况，要么负类样本数大于正类样本数，要么正类样本数大于负类样本数。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而相对于AUC是个数值而言，对应AUC更大的分类器效果更好，数值更好判断一些。

 

首先，解释几个二分类问题中常用的概念：True Positive, False Positive, True Negative, False Negative

它们是根据真实类别与预测类别的组合来区分的.

假设有一批test样本，这些样本只有两种类别：正例和反例。机器学习算法预测类别（左半部分预测类别为正例，右半部分预测类别为反例），而样本中真实的正例类别在上半部分，下半部分为真实的反例。
样本中的真实正例类别总数即TP+FN。True Positive Rate，TPR = TP/(TP+FN)。
同理，样本中的真实反例类别总数为FP+TN。False Positive Rate，FPR=FP/(TN+FP)。

		预测		合计
		1	0
实际	1 (P)	True Positive（TP）	False Negative（FN）	Actual Positive(TP+FN)
	0 (N)	False Positive（FP)	True Negative(TN)	Actual Negative(FP+TN)
合计		Predicted Positive(TP+FP)	Predicted Negative(FN+TN)	TP+FP+FN+TN

还有一个概念叫”截断点”。机器学习算法对test样本进行预测后，可以输出各test样本对某个类别的相似度概率。

比如t1是P类别的概率为0.3，一般我们认为概率低于0.5，t1就属于类别N。这里的0.5，就是”截断点”。
总结一下，对于计算ROC，最重要的三个概念就是TPR, FPR, 截断点。

截断点取不同的值，TPR和FPR的计算结果也不同。将截断点不同取值下对应的TPR和FPR结果画于二维坐标系中得到的曲线

x轴与y轴的值域都是[0, 1]，我们可以得到一组(x, y)的点，相连便作出了ROC曲线，示例图如下：

• 纵坐标是true positive rate(TPR)  = TP / (TP+FN=P) （分母是横行的合计）直观解释：实际是1中，猜对多少
• 横坐标是false positive rate(FPR) = FP / (FP+TN=N)  直观解释：实际是0中，错猜多少

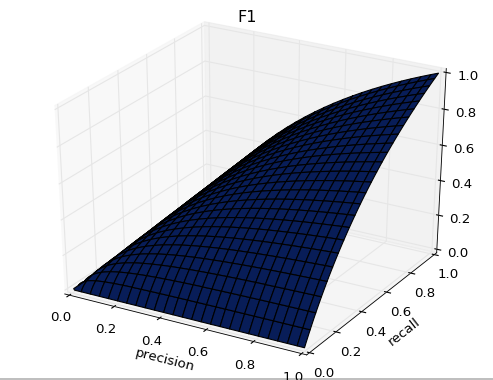
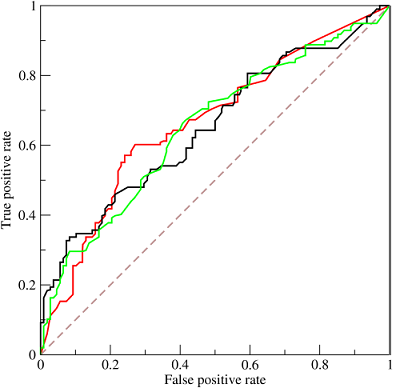
图中的虚线相当于随机预测的结果。不难看出，随着FPR的上升，ROC曲线从原点(0, 0)出发，最终都会落到(1, 1)点。ROC便是其右下方的曲线面积。下图展现了三种AUC的值：

• AUC = 1，是完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。

• 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。

• AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。

• AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测，因此不存在AUC < 0.5的情况

AUC对于每一个做机器学习的人来说一定不陌生，它是衡量二分类模型优劣的一种评价指标，表示正例排在负例前面的概率。其他评价指标有精确度、准确率、召回率，而AUC比这三者更为常用。因为一般在分类模型中，预测结果都是以概率的形式表现，如果要计算准确率，通常都会手动设置一个阈值来将对应的概率转化成类别，这个阈值也就很大程度上影响了模型准确率的计算。

      我们不妨举一个极端的例子：一个二类分类问题一共10个样本，其中9个样本为正例，1个样本为负例，在全部判正的情况下准确率将高达90%，而这并不是我们希望的结果，尤其是在这个负例样本得分还是最高的情况下，模型的性能本应极差，从准确率上看却适得其反。而AUC能很好描述模型整体性能的高低。这种情况下，模型的AUC值将等于0（当然，通过取反可以解决小于50%的情况，不过这是另一回事了）。

ROC 计算例子

from sklearn import  metrics
import numpy as np

y = np.array([1, 1, 2, 2])
scores = np.array([0.1, 0.4, 0.35, 0.8])
fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)
print fpr
print tpr
print thresholds

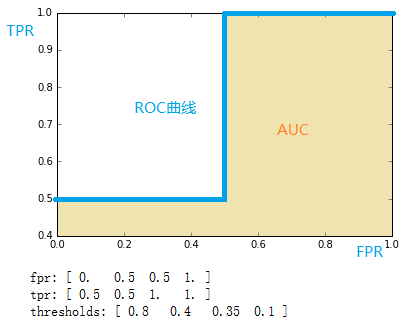
通过计算，得到的结果（FPR,TPR, 截断点）为

[ 0.   0.5  0.5  1. ]
[ 0.5  0.5  1.   1. ]
[ 0.8   0.4   0.35  0.1 ]

将结果中的FPR与TPR画到二维坐标中，得到的ROC曲线如下（蓝色线条表示），ROC曲线的面积用AUC表示（淡黄色阴影部分）。

详细计算过程

上例给出的数据如下:

y = np.array([1, 1, 2, 2])
scores = np.array([0.1, 0.4, 0.35, 0.8])

用这个数据，计算TPR，FPR的过程是怎么样的呢？

1. 分析数据

y是一个一维数组（样本的真实分类）。数组值表示类别（一共有两类，1和2）。我们假设y中的1表示反例，2表示正例。即将y重写为：

y_true = [0, 0, 1, 1]

score即各个样本属于正例的概率。

2. 针对score，将数据排序

样本	预测属于P的概率(score)	真实类别
y[0]	0.1	N
y[2]	0.35	P
y[1]	0.4	N
y[3]	0.8	P

3. 将截断点依次取为score值

将截断点依次取值为0.1,0.35,0.4,0.8时，计算TPR和FPR的结果。

3.1 截断点为0.1

说明只要score>=0.1，它的预测类别就是正例。 
此时，因为4个样本的score都大于等于0.1，所以，所有样本的预测类别都为P。

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1] 
y_pred = [1, 1, 1, 1]

TPR = TP/(TP+FN) = 1 
FPR = FP/(TN+FP) = 1

3.2 截断点为0.35

说明只要score>=0.35，它的预测类别就是P。 
此时，因为4个样本的score有3个大于等于0.35。所以，所有样本的预测类有3个为P（2个预测正确，1一个预测错误）；1个样本被预测为N（预测正确）。

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1] 
y_pred = [0, 1, 1, 1]

TPR = TP/(TP+FN) = 1 
FPR = FP/(TN+FP) = 0.5

3.3 截断点为0.4

说明只要score>=0.4，它的预测类别就是P。 
此时，因为4个样本的score有2个大于等于0.4。所以，所有样本的预测类有2个为P（1个预测正确，1一个预测错误）；2个样本被预测为N（1个预测正确，1一个预测错误）。

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1] 
y_pred = [0, 1, 0, 1]

TPR = TP/(TP+FN) = 0.5 
FPR = FP/(TN+FP) = 0.5

3.4 截断点为0.8

说明只要score>=0.8，它的预测类别就是P。所以，所有样本的预测类有1个为P（1个预测正确）；3个样本被预测为N（2个预测正确，1一个预测错误）。

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1] 
y_pred = [0, 0, 0, 1]

TPR = TP/(TP+FN) = 0.5 
FPR = FP/(TN+FP) = 0

用下面描述表示TPR和FPR的计算过程，更容易记住

• TPR：真实的正例中，被预测正确的比例
• FPR：真实的反例中，被预测正确的比例

最理想的分类器，就是对样本分类完全正确，即FP=0，FN=0。所以理想分类器FPR=0，TPR=0。

第一个点，(0,1)，即FPR=0, TPR=1，这意味着FN（false negative）=0，并且FP（false positive）=0。Wow，这是一个完美的分类器，它将所有的样本都正确分类。

第二个点，(1,0)，即FPR=1，TPR=0，类似地分析可以发现这是一个最糟糕的分类器，因为它成功避开了所有的正确答案。

第三个点，(0,0)，即FPR=TPR=0，即FP（false positive）=TP（true positive）=0，可以发现该分类器预测所有的样本都为负样本（negative）。

第四个点（1,1），分类器实际上预测所有的样本都为正样本。经过以上的分析，我们可以断言，ROC曲线越接近左上角，该分类器的性能越好。