最小二乘法(Least square method)&RANSAC【学习笔记】

一、最小二乘法(Least Square Method)

1.1 线性回归概念【转自百度百科】

  线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为$y = wx+ \varepsilon$，$\varepsilon$为误差服从均值为0的正态分布。

  在统计学中，线性回归（Linear Regression）是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归，大于一个自变量情况的叫做多元回归。（这反过来又应当由多个相关的因变量预测的多元线性回归区别，而不是一个单一的标量变量。）
  在线性回归中，数据使用线性预测函数来建模，并且未知的模型参数也是通过数据来估计。这些模型被叫做线性模型。最常用的线性回归建模是给定X值的y的条件均值是X的仿射函数。不太一般的情况，线性回归模型可以是一个中位数或一些其他的给定X的条件下y的条件分布的分位数作为X的线性函数表示。像所有形式的回归分析一样，线性回归也把焦点放在给定X值的y的条件概率分布，而不是X和y的联合概率分布（多元分析领域）。
  线性回归是回归分析中第一种经过严格研究并在实际应用中广泛使用的类型。这是因为线性依赖于其未知参数的模型比非线性依赖于其未知参数的模型更容易拟合，而且产生的估计的统计特性也更容易确定。
  线性回归模型经常用最小二乘逼近来拟合，但他们也可能用别的方法来拟合，比如用最小化“拟合缺陷”在一些其他规范里（比如最小绝对误差回归），或者在桥回归中最小化最小二乘损失函数的惩罚.相反,最小二乘逼近可以用来拟合那些非线性的模型.因此，尽管“最小二乘法”和“线性模型”是紧密相连的，但他们是不能划等号的。

1.2 最小二乘法(Least Square Method)

1.2.1 三种范数

  假设我们现在有一系列的数据点$(x_{i},y_{i}) (i=1,…,m)$，那么由我们给出的拟合函数$h(x)$得到的估计量就是$h(x_{i})$。
  那么我们就有了残差：$r_{i} = h(x_{i}) – y_{i}$
  由此我们得到三种范数的定义：

1. $\infty$-范数：残差绝对值的最大值，即所有数据点中残差距离的最大值：$\max|r_{i}|(1\le i\le m)$
2. 1-范数：绝对残差和，即所有数据点残差距离之和：$\sum_{i=1}^{m} |r_{i}|$
3. 2-范数：残差平方和：$\sum_{i=1}^{m} r_{i}^2$

1.2.2 最小二乘法【原创详细推导】

  最小二乘法可以理解为通过最小化残差平方和，提升拟合度，以寻找数据的最佳函数描述数据。
  则最小二乘法可用下式表达：

$$LSM = \min_{k,b} \sum_{n=1}^{N}[y_{n}-(k\times x_{n}+b)]^{2}$$

  这是一个无约束的最优化问题，分别对k和b求偏导，然后令偏导数为0，即可获得极值点。

$$d(LSM) = \sum_{n=1}^{N} 2 \times \left [ y_{n}-(k\times x_{n}+b) \right ] (-x_{n} \mathrm{d}k - \mathrm{d}b)$$

则

$$\frac{\partial LSM}{\partial k} = \sum_{n=1}^{N} -2x_{n} \left [ y_{n}-(k\times x_{n}+b) \right ]$$

$$\frac{\partial LSM}{\partial b} = \sum_{n=1}^{N} -2 \left [ y_{n}-(k\times x_{n}+b) \right ]$$

令$\frac{\partial LSM}{\partial k}=0 , \frac{\partial LSM}{\partial b}=0$可得

$$\sum_{n=1}^{N} (k \times x_{n}^2 - x_{n}y_{n} + bx_{n}) = 0 \cdots ①$$

$$\sum_{n=1}^{N} (y_{n} - k \times x_{n}) + bN = 0 \cdots ②$$

由②式得：

$$b = \frac{ \sum_{n=1}^{N} (y_{n}-k \times x_{n})}{N} \cdots ③$$

代入①中，

$$\sum_{n=1}^{N} (k x_{n}^2 - x_{n} y_{n} + \frac{ \sum_{n=1}^{N} (y_{n}-k \times x_{n})}{N} \times x_{n}) = 0$$

等式两端同时$\times N$

$$\sum_{n=1}^{N} (k N x_{n}^2 - Nx_{n}y_{n} + x_{n}\sum_{n=1}^{N} y_{n} - k x_{n} \sum_{n=1}^{N} x_{n}) = 0$$

$$\sum_{n=1}^{N} \left [ k (N x_{n}^2 - x_{n} \sum_{n=1}^{N} x_{n}) - Nx_{n}y_{n} + x_{n}\sum_{n=1}^{N} y_{n} \right ]= 0$$

移项化简之后得到$k$的表达式：

$$k = \frac{N \sum_{n=1}^{N}(x_{n} \times y_{n})-(\sum_{n=1}^{N}x_{n})(\sum_{n=1}^{N}y_{n})}{N\sum_{n=1}^{N}(x_{n})^{2}-(\sum_{n=1}^{N}x_{n})^{2}} \cdots ④$$

  为了简化内容，b的表达式就维持③式的形式，计算时，只需将④代入③即可得到b的表达式。
  即可求得k,b。

1.2.3 局限性

  最小二乘法对误差敏感，如果数据中存在误差较大值，则会影响其拟合效果；
  对于图片而言，其像素点数量大，采用最小二乘法运算量大，计算速度慢。

---

那么有没有一种办法能够优化或者既能一定程度利用LSM的优点又可一定程度规避其缺点呢？

---

二、RANSAC思想

2.1 个人理解

  随机采样一致性(random sample consensus)。一个求解已知模型的参数的框架。 它不限定某一特定的问题，可以是计算机视觉的问题，同样也可以是统计数学，甚至可以是经济学领域的模型参数估计问题。
  我的理解：RANSAC只提供一个解决宏观问题方法，并不提供解决具体问题的方法的一种思想。
  它是一种迭代的方法，用来在一组包含内群(inliers)和离群(outliers)的被观测数据中估算出数学模型的参数。 RANSAC是一个非确定性算法，在某种意义上说，它会产生一个在一定概率下合理的结果，其允许使用更多次的迭代来使其概率增加。

2.2 RANSAC与最小二乘法

  在实际生产活动中，由于环境、生产设备、测量仪器或人工等导致数据中引入误差或偏差等。又由于实际要求，我们又要面临在有限的时间、资源条件下得出“满足要求”的结果。
  除1.2.3所述最小二乘法的局限使其不如RANSAC之外，在模型确定以及最大迭代次数允许的情况下，RANSAC总是能找到最优解(对于包含80%误差的数据集，RANSAC的效果远优于直接的最小二乘法)。

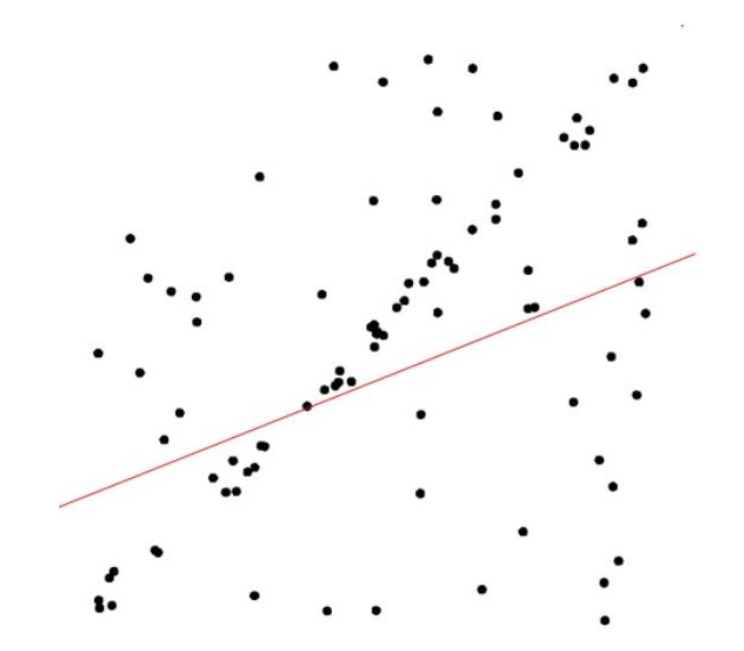
2.3 RANSAC思想的概括

2.3.1 必要的输入

• 一组观测到的数据(可能是预处理过的)；
• 一个可以用来概括或者描述或者被要求验证的模型，例如$y=kx+b$；
• 其他条件或要求，例如残差上限$r_{max}$、最大迭代次数$t_{max}$

2.3.2 实现步骤

1. 随机选取含有$n$个数据点的子集为内群(inliers)，找到使内群点成立的模型中的参数$k,b$；
2. 由上一步确定参数的模型，验证所有其他点，若残差不超过$r_{max}$则认为是内群点，统计内群点数量；
3. 重复上述步骤至最大迭代次数$t_{max}$或者得到足够满意的模型参数等截止条件等
4. 得到相对最佳的模型

2.4 关于$n$和$t$的讨论

  一定会有带着困惑的烦恼看到这里的小伙伴，他们会纠结残差上限$r_{max}$、最大迭代次数$t_{max}$和随机选取被认定是内群点的数量$n$究竟设定为多少才合适？
  残差上限$r_{max}$一般是结合实际要求或者经验，在项目的初始就能够得到的要求，因此不必纠结。那么剩下就是关于$n$和$t$的讨论：



  前提条件$n \le n_{inliers}$，否则下述推导将出现bug。
  设随机选取一个点为真实内群点的概率为$w$，那么：

$$w=\frac{n_{inliers}}{n_{inliers}+n_{outliers}}$$

  由此可得，随机选取的含有$n$个点的集合为真实内群子集的概率为：$w^{n}$
  而$1-w^{n}$即选取的集合中含有至少1个离群点(outliers)的概率
  假设经过$t$次迭代，没有任何一次迭代所选取的集合为真实内群子集的概率为：$(1-w^{n})^t$
  那么$t$次迭代中至少有1次成功选取到真实内群子集的概率(p)为：

$$p=1-(1-w^{n})^t$$

  通常$n_{inliers}$未知，因此$w$未知，但在给定数据集时可以合理地认为这是一个确定的数。

• 当$n$一定的条件下，$t↑\Rightarrow p↑$，即可通过增加迭代次数以提高选取到真实内群子集的概率
• 当$t$一定的条件下，$n↓\Rightarrow p↑$，即可通过降低$n$以提高选取到真实内群子集的概率

  P.S.同时应当注意，在确定模型参数时所用到的正是随机选取的含有$n$个点的集合，因此必须保证$n$不能太小，否则或者无法确定参数，或者不同迭代次数的子集拟合到相同或过于相近的参数导致产生无效迭代(假设$n=2$，数据集中存在三点共线，某三次迭代中的数据集合恰巧为三点中的两个点，实际拟合为同一条直线方程)。

2.5 RANSAC的优缺点

优点：

1. 它能鲁棒的估计模型参数。例如，它能从包含大量局外点的数据集中估计出高精度的参数。

缺点：

1. 它计算参数的迭代次数没有上限；如果设置迭代次数的上限，得到的结果可能不是最优的结果，甚至可能得到错误的结果。
2. RANSAC只有一定的概率得到可信的模型，概率与迭代次数成正比。
3. 它要求设置跟问题相关的阀值。
4. RANSAC只能从特定的数据集中估计出一个模型，如果存在两个（或多个）模型， RANSAC不能找到别的模型。
5. 要求数学模型已知

扩展阅读

  博主在写完自己的上述笔记之后也阅读了一些其他文章，觉得不够解渴的朋友也可以参考下面文章~

1.一文让你彻底搞懂最小二乘法（超详细推导）

2.最小二乘法 来龙去脉

3.最小二乘法——线性回归背后的数学，探究其公式的诞生过程

4.RANSAC基本原理

5.RANSAC算法理解

6.我的数学之美（一）——RANSAC算法详解