数字图像学习——双线性插值方法部分的讨论

写在前面：

  双线性插值在数字图像中属于基础中的基础，然而在解决课后作业问题中却发现“熟知≠真知”的情况，故两个星期反复推导、提问和沟通。决心写下笔记，供自己日后复习，也希望拿出来与同学和老师共同交流、接受批评指正，最终实现进步！
【同内容文章本人稍早前发布于CSDN】数字图像学习——双线性插值方法部分的讨论【个人详细推导】

一、准备工作：

1.1 认清几个事实：

(I) 数字图像在计算机中是以矩阵形式储存，其行列下角标从0开始
(II) 矩阵中每个元素中储存对应数字图像中的像素值(可能不只一个通道)
(III) 矩阵中元素信息对应数字图像对应位置中的位置和像素值信息，却不包含实际图像中像素点本身大小
(IV) 将图像放置于坐标系中，y轴正方向向下，x轴正方向向右

1.2提出几个设定：

(i) 下述讨论中，为了便于理解，假设所有图像中的像素点均为边长1的正方形
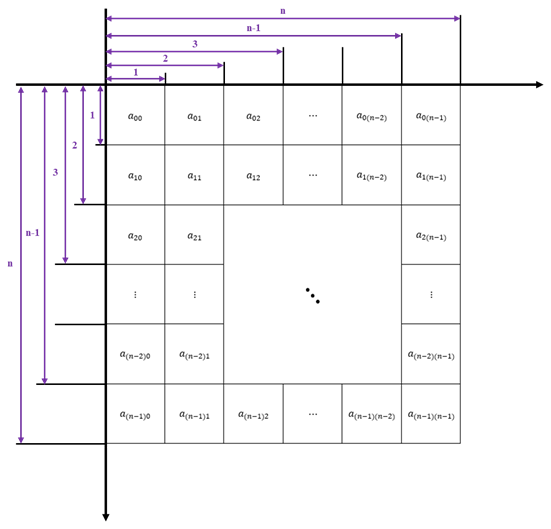
(ii) 原图像尺寸(H=m, W=n)，原图像矩阵 \(A_{m\times n}\)
\(A_{m \times n}=\begin{bmatrix}a_{00} &a_{01} &\cdots &a_{0(n-1)} \\a_{10} &a_{11} &\cdots &a_{1(n-1)} \\\vdots &\vdots &\ddots &\vdots \\a_{(m-1)0} &a_{(m-1)1} &\cdots &a_{(m-1)(n-1)} \\\end{bmatrix}\)
\(a_{ij}\in [0,255]\cap a_{ij}\in N(i=0,1⋯(m-1),j=0,1⋯(n-1))\)
(iii) 原图像中各点像素值(矩阵中元素值)与位置坐标满足映射 \(a_{ij}=f(i,j)\)

Fig 1 数字图像与对应矩阵图示

二、坐标变换讨论：

2.1原图像、目标图像和插值点阵

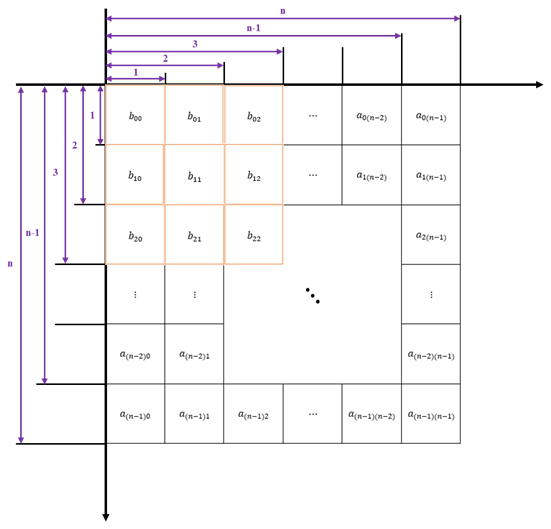
  设：目标图像尺寸(H=r, W=s), 图像矩阵\(B_{r \times s}=\begin{bmatrix}b_{00} &b_{01} &\cdots &b_{0(s-1)} \\b_{10} &b_{11} &\cdots &b_{1(s-1)} \\\vdots &\vdots &\ddots &\vdots \\b_{(r-1)0} &b_{(r-1)1} &\cdots &b_{(r-1)(s-1)} \\\end{bmatrix}\)

\[b_{ij}\in [0,255]\cap b_{ij}\in N(i=0,1⋯(r-1),j=0,1⋯(s-1)) \]

  因此y方向(即H方向)变换比例为\({\color{blue}{k_{m\rightarrow r}=\frac{r}{m}\cdots ①}}\)
  同理x方向(即W方向)变换比例为\({\color{blue}{k_{n\rightarrow s}=\frac{s}{n}\cdots ②}}\)
  那么在进行插值之前，我们就要试图找到图像B中各像素点与图像A中各像素点的“某种’位置’对应关系”，在此对应关系基础上，才可以应用插值算法。

  那么位置对应关系如何建立？

  我们很自然地认为只需要将B中像素坐标做变换\({\color{blue}{\left\{\begin{matrix} y_{b}\times\frac{1}{k_{m\rightarrow r}}=y_{M} \\ x_{b}\times\frac{1}{k_{n\rightarrow s}}=x_{M} \end{matrix}\right.\cdots ③}}\)
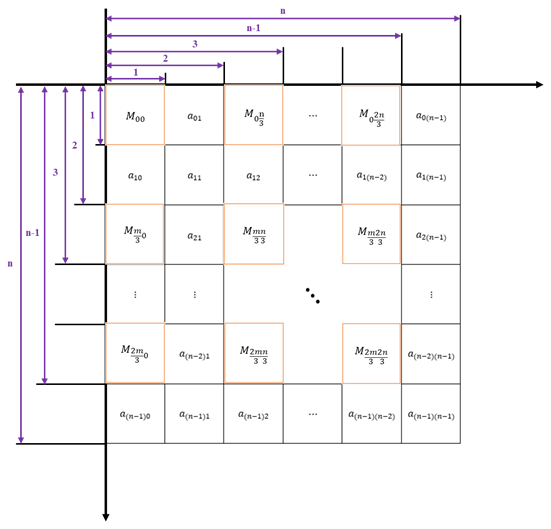
  即得到\(M(y_{M},x_{M})\)为\((y_{b},x_{b})\)的插值点与A中相关的4个点进行插值运算。
  不过！请稍作思考，我们就会发现由于上述事实和假设的存在，图像缩放比例与坐标比例之间存在差异会导致我们的坐标按照③式变换后得到B的插值点阵\(M_{r\times s}\)的坐标偏向左上角且与A于左上角对齐。这会带来“不可接受”的偏差，因此我们需要消除。

  那么，\(M_{r\times s}\)的坐标到底要如何做？

Fig 2 缩放前后数字图像与对应矩阵图示

Fig 3 图像B经比例变换后的点阵M与其矩阵图示

2.2几何中心的对齐

  也许解决这个问题的思路之一就是“修正”\(M_{r\times s}\)的坐标，方法就是对齐进行坐标平移变换使二者几何中心坐标相等，即所谓对齐。

  那么，平移向量如何取？

  我们不妨以y轴方向(H方向)举例推导，x轴方向同理。
  原图像几何中心坐标\({\color{blue}{y_{A0}=\frac{1}{2}(m-1)\cdots ④}}\)
  图像B的插值点阵\(M_{r\times s}\)几何中心坐标\({\color{blue}{y_{M0}=\frac{1}{2}(r-1)\times \frac{1}{k_{m\rightarrow r}}=\frac{1}{2}(r-1)\times\frac{m}{r} \cdots ⑤}}\)
  无论向量直接对A、直接对B、直接对M或者对A、B同时平移，在数学上均可以推导出大家在很多文章中看到的“左右各\(+\frac{1}{2}\)”的形式，下面是直接对M平移的推导过程：
  设：对M平移k个单位与A对齐，则根据④=⑤+k式可以得，

\[{\color{blue}{y_{A0}=y_{M0}+k\cdots⑥}} \]

\[\frac{1}{2}(m-1)=\frac{1}{2}(r-1)\times\frac{m}{r}+k \]

\[k=\frac{1}{2}(m-1)-\frac{1}{2}(r-1)\times\frac{m}{r} \]

\[k=\frac{1}{2}[(m-1)-(r-1)\times\frac{m}{r}] \]

\[k=\frac{1}{2}[\frac{r(m-1)-mr+m}{r}] \]

\[k=\frac{1}{2}[\frac{m}{r}-1]=\frac{1}{2}\times \frac{m}{r}-\frac{1}{2} \]

  将k值代回⑥到得，

\[y_{A0}=y_{M0}+\frac{1}{2}\times \frac{m}{r}-\frac{1}{2} \]

\[y_{A0}+\frac{1}{2}=y_{M0}+\frac{1}{2}\times \frac{m}{r} \]

\[y_{A0}+\frac{1}{2}=y_{B0}\times \frac{m}{r}+\frac{1}{2}\times \frac{m}{r} \]

\[{\color{blue}{y_{A0}+\frac{1}{2}=(y_{B0}+\frac{1}{2})\times \frac{m}{r} \cdots⑦}} \]

  看！我们成功得到的大家在资料中看到的⑦式同样形式的“左右各\(+\frac{1}{2}\)”的结论！
  但是，请注意！不要过度喜出望外，还记得我们仅仅是将“M几何中心坐标通过坐标平移变换与A的几何中心坐标重合”了么？

  那么，M中其他坐标变换后的坐标表达式是什么呢？

2.3关于插值点阵所对应矩阵中坐标的讨论(目前没有看到类似文章讨论)

2.3.1 平移后插值点阵所对应矩阵坐标\(y_{T}\)的取值范围

  根据上一节知，我们对M中坐标进行平移变换，变换后得到新的插值点阵\(T_{r\times s}\)，则

\[y_{T}=y_{M}+\frac{1}{2}(\frac{m}{r}-1) \]

\[y_{T}=y_{B}\times \frac{m}{r}+\frac{1}{2}(\frac{m}{r}-1) \]

Fig 4 点阵M经过坐标平移变换T的插值点阵与矩阵坐标图示

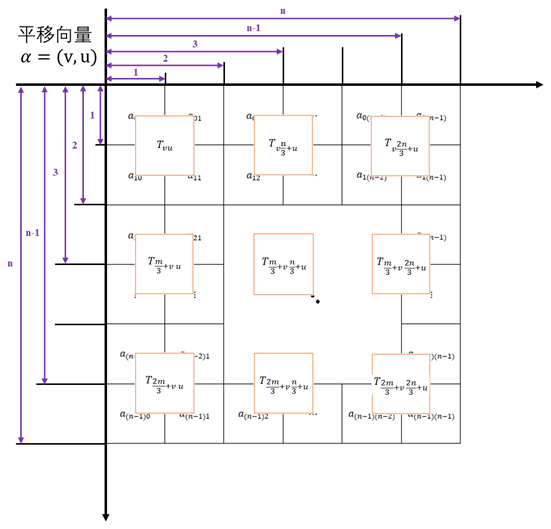
  由于\(y_{B}\in [0,(r-1)]\)，我们可以得到y方向插值点阵\(T_{r\times s}\)的坐标取值范围为

\[{\color{blue}{y_{T}\in [\frac{1}{2}(\frac{m}{r}-1),(r-1)\times \frac{m}{r}+\frac{1}{2}(\frac{m}{r}-1)]\cdots⑧}} \]

2.3.2 平移后插值点阵的矩阵坐标\(y_{T}\)的取值范围边界的分类讨论

  设：\(f(r)=\frac{1}{2}(\frac{m}{r}-1)\)，\(g(r)=(r-1)\times \frac{m}{r}+\frac{1}{2}(\frac{m}{r}-1)\)，则\(y_{T}\in [f(r),g(r)]\)
  (1).如果目标图像B相对原图像A是放大，则\(r\in [m+1,+\infty )\)

\[\because f^{'}(r)=-\frac{m}{2r^{2}}<0, \therefore f(r)\in (-\frac{1}{2},-\frac{1}{2(m+1)}] \]

  即\(y_{T}\in (-\frac{1}{2},-\frac{1}{2(m+1)}]\)落在原图像“最小坐标”之外，它与落在原图像之内的点在进行双线性插值的时候算法上将会有差别。

  P.S.那么等价矩阵中只有最小值\(y_{T,min}\)在原图像最小坐标之外么？

  我们来验证一下：设：\(\triangle y\in N^{+}\)，令

\[y_{T,min+\triangle y} =(0+\triangle y)\times \frac{m}{r}+\frac{1}{2}(\frac{m}{r}-1)\ge 0 \]

\[\triangle y\ge \frac{1}{2}(\frac{r}{m}-1)>\frac{1}{2}(\frac{m+1}{m}-1)=\frac{1}{2m} \]

\[\frac{1}{2m}\in (0,\frac{1}{2}], \triangle y_{min}\le 1 \]

  又

\[\because \triangle y\in N^{+}, \therefore \triangle y_{min}=1 \]

  翻译翻译就是：y轴负方向上有且仅有\(y_{T,min}\)在原图像“最小坐标”之外。
  下面我们进行对上限取值范围的讨论：

\[\because g^{'}(r)=\frac{m}{2r^{2}}>0, \therefore g(r)\in [m-1+\frac{1}{2(m+1)},m-\frac{1}{2}) \]

\[g(r)_{min}-(m-1)=m-1-(m-1)+\frac{1}{2(m+1)}=\frac{1}{2(m+1)}>0 \]

  即\(y_{T,max}\in [m-1+\frac{1}{2(m+1)},m-\frac{1}{2})\)落在原图像“最大坐标”之外，它与落在原图像之内的点在进行双线性插值的时候算法上将会有差别。(此时要注意我们已经证明了插值点阵中的四个角点更加特殊)

  P.S.那么等价矩阵中只有最小值\(y_{T,max}\)在原图像最大坐标之外么？

  我们来验证一下：设：\(\triangle y\in N^{+}\)，令

\[y_{T,max-\triangle y}-(m-1)=(r-1-\triangle y)\times \frac{m}{r}+\frac{1}{2}(\frac{m}{r}-1)-(m-1)\ge 0 \]

\[(r-1-\triangle y)\times \frac{m}{r}+\frac{1}{2}(\frac{m}{r}-1)-(m-1)\ge 0 \]

\[\frac{1}{2}(\frac{r}{m}-1)\ge \triangle y \]

\[\frac{1}{2}(\frac{r}{m}-1)\in [\frac{1}{2m},+\infty )>0, \therefore \triangle y_{min}\le 1 \]

  又

\[\because \triangle y\in N^{+}, \therefore \triangle y_{min}=1 \]

  翻译翻译就是：y轴正方向上有且仅有\(y_{T,max}\)在原图像“最大坐标”之外。

  (2).如果目标图像B相对原图像A是缩小，则\(r\in [1,m-1]\)(注意m>\({\color{red}{2}}\))

\[\because f^{'}(r)=-\frac{m}{2r^{2}}<0, f(r)\in [\frac{1}{2(m-1)},\frac{1}{2}(m-1)]>0 \]

\[y_{T,min}-0>0 \]

  即y轴负方向上\(y_{T,min}\)在原图像“最小坐标”之内。

  下面我们进行对上限取值范围的讨论：

\[\because g^{'}(r)=\frac{m}{2r^{2}}>0, \therefore g(r)\in [\frac{1}{2}(m-1),(m-1)-\frac{1}{2(m-1)}] \]

\[g(r)_{max}-(m-1)=-\frac{1}{2(m-1)}<0 \]

  即y轴正方向上\(y_{T,max}\)在原图像“最大坐标”之内。
  其余情况，如变换比例为1或原图(H=W=2)缩小为新图(H=W=1)等情况不作讨论。
  至此关于插值点阵\(T_{r\times s}\)中矩阵坐标的讨论结束！

三、双线性插值思路和方法讨论：

3.1线性插值原理(个人理解版)3.1线性插值原理(个人理解版)

  (为了避免与前几章相关名词或符号相混淆，也为了更适合接下来的讨论，本人对线性插值介绍的一些名词和符号做了调整。)
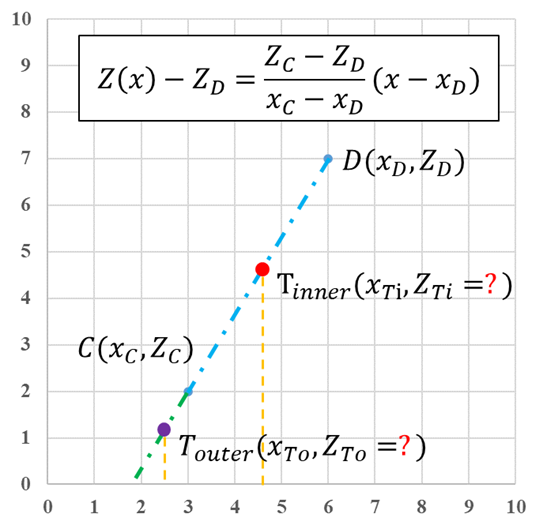
  设：平面直角坐标系中存在已知的两点坐标分别为\(C(x_{C},Z_{C})\)和\(D(x_{D},Z_{D})\)(两点横纵坐标各不相等)，已知另外两个横坐标\(x_{Ti},x_{To}\)
  求：当\(T_{inner}(x_{Ti},Z_{Ti})\)和\(T_{outer}(x_{To},Z_{To})\)在CD两点所在所确定的直线上时的坐标。
  我们知道，如果点在直线上，那么该点坐标一定满足该直线方程。
  首先求该直线方程，根据点斜式可知：

\[{\color{blue}{Z(x)-Z_{D}=\frac{Z_{C}-Z_{D}}{x_{C}-x_{D}}(x-x_{D})\cdots ⑨}} \]

  只需将\(x_{Ti},x_{To}\)带入⑨式即可求得两点坐标。

Fig 5 线性插值原理图示

3.2双线性插值原理(个人理解版)

  即使用3次线性插值，其中前两次插值所得到的点所确定的直线用于第三次插值。
  已知原图像中点\((y_{ij},x_{ij})\)的像素值满足\(f(y_{ij},x_{ij})\)，那么图6中欲通过双线性插值得到点T的像素值，就需要先通过两次线性插值得到\(P_{inner}\)和\(Q_{inner}\)的像素值，即

\[g_{up}(y_{up},x_{ij})-f(y_{up},x_{lf})=\frac{f(y_{up},x_{rt})-f(y_{up},x_{lf})}{x_{rt}-x_{lf}}(x_{ij}-x_{lf}) \]

\[{\color{green}{g_{up}(y_{up},x_{ij})}}=\frac{f(y_{up},x_{lf})(x_{rt}-x_{ij})-f(y_{up},x_{rt})(x_{ij}-x_{lf})}{x_{rt}-x_{lf}} \]

  同理可得，

\[{\color{green}{g_{dn}(y_{dn},x_{ij})}}=\frac{f(y_{dn},x_{lf})(x_{rt}-x_{ij})-f(y_{dn},x_{rt})(x_{ij}-x_{lf})}{x_{rt}-x_{lf}} \]

Fig 6 双线性插值过程图示
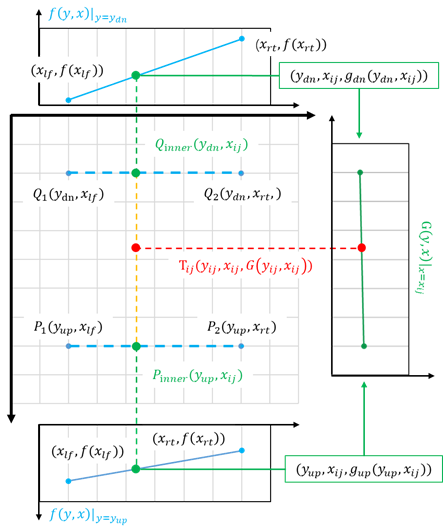
  则做第三次线性插值

\[{\color{red}{G(y_{ij},x_{ij})}}=\frac{{\color{green}{g_{dn}(y_{dn},x_{ij})}}(y_{up}-y_{ij})-{\color{green}{g_{up}(y_{up},x_{ij})}}(y_{ij}-y_{dn})}{y_{up}-y_{dn}} \]

  如果考虑实际情况，则有\({\color{blue}{x_{rt}-x_{lf}=1}}\)且\({\color{blue}{y_{up}-y_{dn}=1}}\)，那么

\[ \left\{\begin{matrix} {\color{green}{g_{up}(y_{up},x_{ij})}}=f(y_{up},x_{lf})(x_{rt}-x_{ij})+f(y_{up},x_{rt})(x_{ij}-x_{rf}) \\ {\color{green}{g_{dn}(y_{dn},x_{ij})}}=f(y_{dn},x_{lf})(x_{rt}-x_{ij})+f(y_{dn},x_{rt})(x_{ij}-x_{rf}) \\ {\color{red}{G(y_{ij},x_{ij})}}={\color{green}{g_{dn}(y_{dn},x_{ij})}}(y_{up}-y_{ij})+{\color{green}{g_{up}(y_{up},x_{ij})}}(y_{ij}-y_{dn}) \end{matrix}\right.\cdots ⑩ \]

  经过代入化简可以得到某些资料上的那个“四项式”(下述紫色部分式子)：

\[{\color{red}{G(y_{ij},x_{ij})}}=Term1 + Term2 + Term3 + Term4 \]

\[Term1=f(y_{dn},x_{lf})(x_{rt}-x_{ij})(y_{up}-y_{ij})\Leftrightarrow {\color{purple}{(1-u)\cdot (1-v)\cdot f(i,j)}} \]

\[Term2=f(y_{dn},x_{rt})(x_{ij}-x_{lf})(y_{up}-y_{ij})\Leftrightarrow {\color{purple}{u\cdot (1-v)\cdot f(i+1,j)}} \]

\[Term3=f(y_{up},x_{lf})(x_{rt}-x_{ij})(y_{ij}-y_{dn})\Leftrightarrow {\color{purple}{(1-u)\cdot v\cdot f(i,j+1)}} \]

\[Term4=f(y_{up},x_{rt})(x_{ij}-x_{lf})(y_{ij}-y_{dn})\Leftrightarrow {\color{purple}{u\cdot v\cdot f(i+1,j+1)}} \]

  计算机代码中可直接使用⑩式计算插值即可。

3.3双线性插值实际应用时对特殊情况的处理

  情况一：比例为1的缩放
  如果遇到图片缩放比例为1时，考虑功耗和代码运行效率等，虽然此时仍可以无障碍运行插值算法代码程序，但仍建议代码中在判定成功时，直接copy原图像直接输出。
  情况二：放大图像
  从双线性插值原理我们不难得知，所有插值是假设使用“内插值”。虽然数学上我们同样可以使用4个点阵对点阵外一点使用“外插值”，但是在实际计算机处理大量数据时，其常常是采用循环语句进行批量处理，因此不可避免需要增加判断语句代码，对外插值情况编写单独算法。
  例如2.3.2的结论，在图像放大时，等价点阵的最外层的一圈点的矩阵坐标在原图像矩阵坐标“外侧”。因此对于四个角上的点，我们需要单独以原图像对应的四角方格的4个点阵做外插值；而对于四条边上的点，则需要选取最临近的一个方格的4个点做外插值。

四、总结：

  \(T_{r\times s}\)无论百度或者知乎等关于“双线性插值”的介绍都集中于对基础数学原理的简单推导和“为什么要在等式两端\(+\frac{1}{2}\)”做简单推导。
  而本笔记针对作业中实际问题作更加细致的讨论，所涉及到运用的知识为高中或者大一的数学知识，作图部分仅靠office家族即可完成。公式推导部分更加详细且整洁，图示信息更加丰富且易读。
  本笔记并没有将得到的结论应用于代码实践中，原因在于：可实现算法的编程语言众多，如C++、Java或者python等不便于也没能力逐一展示。但通过上述几章的讨论，我们已经知道了当解释器报错或者输出结果不堪入目的时候，有可能就是我们的代码在处理数学结果上没有同样分类处理所造成的。
  需要指出的是，不同人提出的处理方法各不相同，也有可能提出的新解决方法的同时也引入的新的问题。这就要求我们对不同解决方案之间评估风险，做出取舍……一切以“最适合”解决所面临的问题为最优先。
  鉴于本笔记是在作者七次推导失败后形成的，相信一定仍存在漏洞，甚至是错误。请大家一定多提问题，对任何错误及时加以批评指正！
  谢谢大家！永远支持原创！

  P.S.吐槽一下markdown写公式搭进去半条命，排版又搭进去剩下半条命,又找隔壁王二狗借了半条命给公式内的特殊项上色……囧