搜索树
2-3树
首先说明个问题,为什么需要2-3树?
使用二叉树作为便于查找和修改的数据结构,继承了有序数组通过二分查找实现查找的速度,和继承了基于链表操作符号表的速度。也就是说我们可以通过实现二叉树的方式实现符号表可以继承有序数组和链表实现符号表的优点而不继承他们的缺点,因为数据和链表的优势是互补的。
但是想要二叉树实现几乎等同于基于有序数组的二分查找速度,那么就需要二叉树左子树和右子树相对平衡。但是二叉树的生成无法保证左子树和右子树的平衡性。例如顺序插入键值为【1,2,3,4,5,6,7,8,9】生成的二叉树等同于链表。那么二叉树查找的时间复杂度和链表差不多。这时候二叉树就没有意义,所以我们要有一种方法在生成二叉树的时候保持二叉树整体的平衡性,但是也要保持二叉树整体的有序性。
2-3树指的是一棵树:如果它的结点只有一个键值两条链接那么这就是2-结点,如果有两个键值,小键值在左边,大键值在右边,并且右三个链接,这就是3-结点,左连接指向小于两个键值的结点,右链接指向大于两个键值的结点,中链接指向[小键值,大键值]这个区间的结点。链接一个空结点的时空链接。

2-3树是如何保持树的平衡性的?
2-3树的生长方法不同于二叉树,一般二叉树是向下生长,而2-3树是向上生长,这样保持了叶子结点的都在同一层上.每一层的结点到root结点的路径长度是一致的.
局部性:
当插入结点或者删除结点的时候,只有与这个操作相关的结点需要变动,不涉及其他结点.
全局性:
当插入结点或者删除结点时,整棵树要么同时变高,要么同时变矮.
2-3树的操作
插入
-
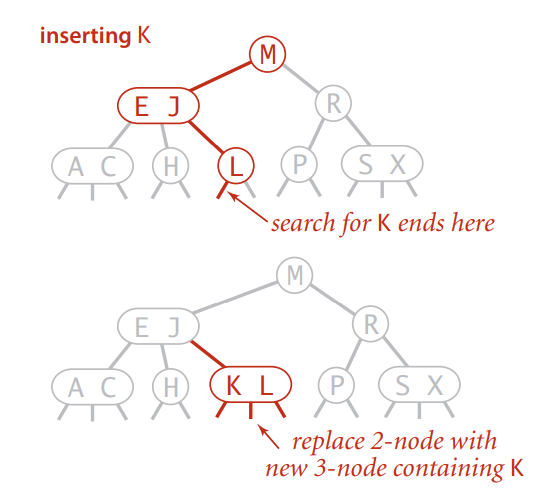
向2-结点插入
如果插入的结点是2-链接结点的话,那么就要把这个结点变为3-链接结点就好了.
-
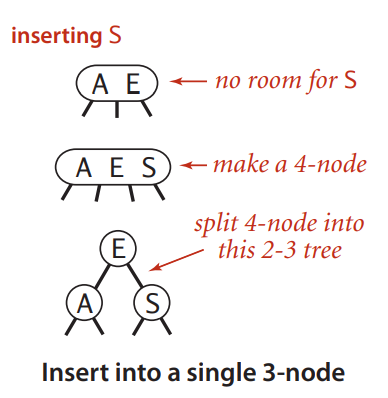
向一个3-链接结点插入
首先向3-链接结点插入键值,变成3键值4链接结点,然后提取中间键作为这个3键值做作为另外两个键的父结点,生成一棵完全二叉树. 插入前树的高度是0,插入后树的高度是1.这个体现了2-3树的生成规律.
-
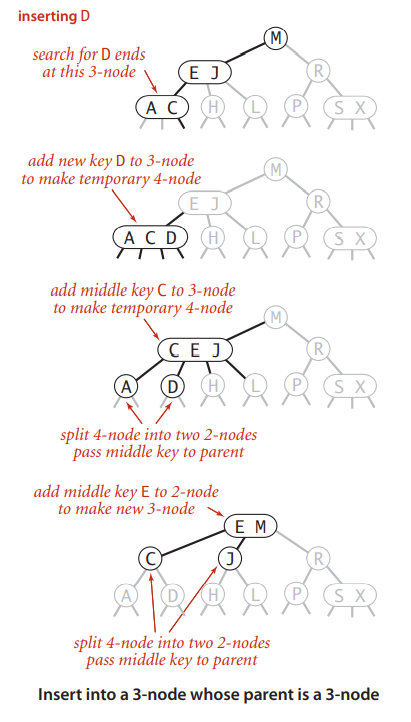
向一个父节点是2-结点的3-结点插入键值
也是把3-结点先变成4-结点,然后也是生成一个完全二叉树,再把这个二叉树的root结点传给3-结点的父2-结点,让这个父2-结点变为3-结点。

-
向一个父节点为3-结点的3-结点插入结点
还是相同的,将3-结点变为4-结点在变成完全二叉树,把完全二叉树的root结点传给父3-结点.父3-结点也变成4-结点.再变成一颗完全二叉树,并且树高+1.
-
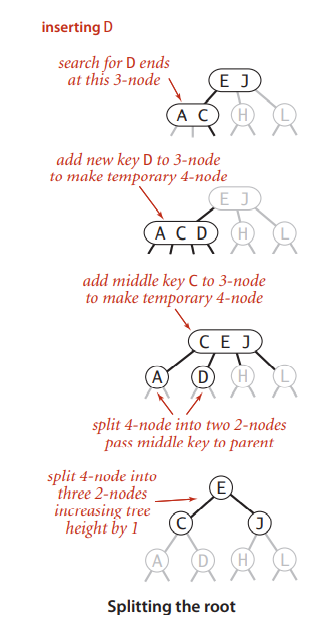
分解root结点
如果从更路径到添加结点的路径都是3-结点,那么最后,root会变成一颗平衡二叉树.树高+1
红黑树的删除操作
红黑树的删除操作和插入操作都是有一个同样的目的,就是做完操作之后,树要保持平衡。
我们先说明下红黑树的性质:
1.红链接均为左链接
这个是为了与2-3树对应,简化红黑树的实现.当然也可以有红链接是右链接的方式.
2.不可以有两个连续做红链接.
这个也是与2-3树对应,如果右连续两个红链接那么与2-3树对应的话就是一个4-结点.
3.红黑树的完美平衡的,就是任意一个空连接到root的黑色链接的数量是一致的.
这个是最重要的.
插入操作时,为了保持红黑树的平衡性,那么我们要做的就是为插入操作所影响的结点插入一条红链接。这个操作意味着将一个2-结点变为了3-结点。
删除操作时,为了保持红黑树的平衡性,我们要做的就是先删除红链接来保持树的平衡性。这个意味着将一个3-,或者临时的4-结点变为了一个2-或者3-结点。删除红链接并不会影响树的平衡性。
由于插入操作和上面的2-3树的插入一致,代码也不难理解,所以略过,只记录删除操作。
为了保持红黑树的平衡性,那么我们删除一个结点的时候,一定要保证它不是2-结点。这是最重要的,即使要删除的结点不是2-结点,为了防止意外我们还是要做一些保证性的变化。
这里先理解deleteMin()的删除操作,再去理解deleteMax()和delete()的时候会简单很多。
删除最小结点
root的情况
首先从root结点开始,如果root结点的左结点,和右结点的链接都是黑色的,那么这个由root和它结点构成的完全二叉子树是由插入操作子树向上传递红链接导致的生成的root的4-结点,插入操作将它拆分,使树高+1。
所以在删除操作时,我们要将它变化回去。变成拆分前的临时4-结点。所以删除操作可以看成插入操作的逆过程。所以开始删除之前我们要将root的颜色置为红色。
public void deleteMin(){
//上面加深字体是这个理解.
if(isBlack(root.left)&&isBlack(root.right)){
root.color = RED;
}
}
root除了将3个2-链接结点还原成临时的4-结点,还要考虑到其他的情况。
例如:
左节点是2-结点,右结点不是2-结点,那么我们就要进行变化确保左节点不是2-结点,可以从父节点借位,父节点借键后的空缺由兄弟结点的键填补。
如果父节点不是2-结点,但是左节点和右结点都是2-结点,那么我们可以取父节点中最小的键,与两个子节点生成一个临时的4-结点。
为什么一定是左结点,这是因为这时我们只考虑删除最小键的情况,最小键在左子树。
具体变化如图:
3个2-结点变为4-结点: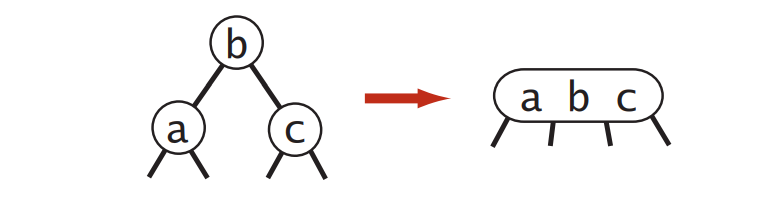
其他情况: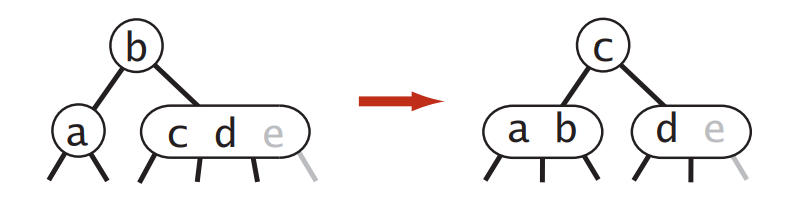
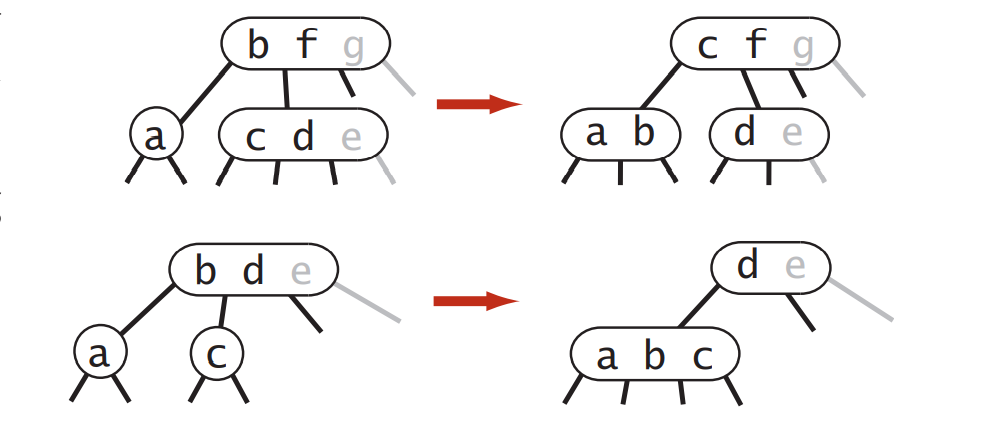
下沿子树的变化情况
- 如果左连接不是红链接,也就是说左结点不是2-链接结点,那么继续向下找,
- 如果左节点是2-结点兄弟不是,那么处理情况和root的一致,逆向还原,将2-变为3-或者4-。
- 如果左节点和右结点时2-结点,但是父节点是3-,4-结点的话,取父结点中的最小键,然后让它和左右子节点生成4-链接结点。
private node<K,V> deleteMin(node<K, V> h, K key){
//这个就是删除操作了
if(Object.isNull(h.left)){
return null;
}
if(isBlack(h.left) && isBlack(h.left.left)){
//将左节点变成3-结点或者4-结点
h = moveRedLeft;
}
h.left = deleteMin(h.left, key);
h.N = size(h.left) + size(h.right) + 1;
return balance(h);
}
private node<K, V> moveRedLeft(node<K,V> h){
/*
首先能进入这里,就说明了h结点的左连接是2-结点,那么我们就要把左连接结点变为红色.
首先,我们不管右连接结点是什么情况,即使右连接不是2-结点,变红都是必要步骤,
如果左结点时2-结点,那么与它一起生成的3-结点的键一定时父节点中最小键就是它的后继结点。
所以只要左连接结点时2-结点,这部都不是多余的。
给右结点一起变红可能是一个多余的步骤,对于向下查找而言,但是对于root的第一种情况,
就是3个2-结点的情况,这个就不是多余的了,通过冗余操作提高代码的复用率也不是不可。
那么问题来了,如果右结点是3-结点,那么h将指向右结点的连接变红不会有问题吗?
不会,因为通过下面的右旋加左旋操作,到最后,置红的链接变为了root的红链接,
root最后会被置黑,所以操作上是没有问题的。
*/
flibColors(h);
if(isRed(h.right.left)){
h.right = rotateRight(h.right);
h = rotateLeft(h);
}
return h;
}
删除最大结点
删除最大结点本质和删除最小节点是一样的。不过需要多余的一步,那就是将红链接右旋。变成一个红链接在右边的红黑树。这是因为,原本的定义中,红链接用于在左边,所以右节点不会有3-结点。最大键一定在最右边。所以这个操作是必要的。·
private node<K,V> deleteMax(node<K,V> h, K key){
//删除键前要先变换。
if(isRed(h.left)){
h = rotateRight(h);
}
if(Objects.isNull(h.right)){
return null;
}
-------------------------------
剩下的都一样了.
}
删除操作
删除操作就是删除deleteMin()和deleteMax()方法的结合。
如果key < h.key 那么就是做moveRedLeft操作,保证左子结点是3-或者4-结点。
如果key > h.key 那么就是左moveRedRgiht操作,保证右子结点时3-或者4-结点。
如果key == h.key 那么我们不删除该结点,而是用改结点的后继结点取代该节点的位置。然后我们删除原来位置的后继结点,通过deleteMin()实现。
private node<K, V> delete(node<K,V> h, K key){
if(lessThan(key, h.key)){
if(isBlack(h.left) && isBlack(h.left.left)){
h = moveRedLeft(h);
}
h.left = delete(h.left, key);
}else{
if(isRed(h.left)){
h = rotateRight(h);
}
if(isBlack(h.right) && isBlack(h.right.left)){
h = moveRedRight(h);
}
if(key.equals(h.key)){
n.val = get(h.right, min(h,right).key);
n.key = min(h.right).key;
/*
二叉树的删除时具有局部性的,就是只影响相关的结点.
而且红黑树的删除绝对不会对平衡性有什么影响,因为删除的链接时红链接,
也就是说删除的3-结点的或者4-结点中的一个键.
*/
h.right = deleteMin(h.right);
}
else h.right = delete(h.right);
}
return balance(h);
}



