力扣_中级算法_链表_第3题_和_树和图_第1~3题

一位C++小白的力扣刷题_成长记录_welcome to visit  ^_^  

 

链表_第3题：相交链表

题目描述：

编写一个程序，找到两个单链表相交的起始节点。

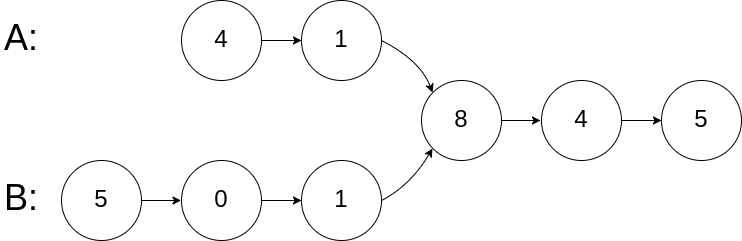
如下面的两个链表：

在节点 c1 开始相交。

 

举例

示例 1：

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Reference of the node with value = 8
输入解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

 

示例 2：

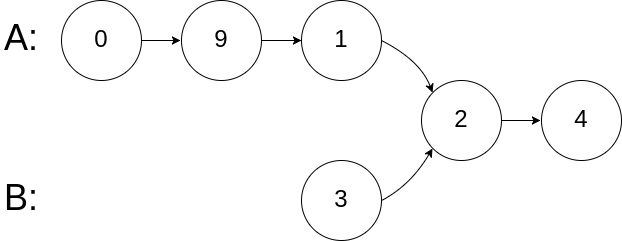
输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Reference of the node with value = 2
输入解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

 

示例 3：

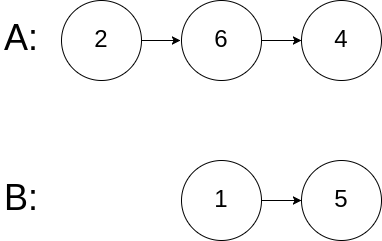
输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
输入解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
解释：这两个链表不相交，因此返回 null。

 

注意：

• 如果两个链表没有交点，返回 null.
• 在返回结果后，两个链表仍须保持原有的结构。
• 可假定整个链表结构中没有循环。
• 程序尽量满足 O(n) 时间复杂度，且仅用 O(1) 内存。

解题思路：如果把时间复杂度放宽一点，就比较简单，两层 for 循环就可以搞定。但如果要限制时间复杂度。就要巧妙地调用指针。

学习心得：简单的方法总是比较容易想到。高级点的方法，需要一点积累与直觉呢。看了这道题 的优秀的

题解，让我感觉到了 指针 的魅力。真的，指针提高了很多效率。

 

 

实现：（C++）

/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
　　public:
　　　　ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
　　　　ListNode *h_A=headA; //定义一个在 链表1上移动的指针
　　　　ListNode *h_B=headB; //定义一个在 链表2上移动的指针
　　　　if( headA==NULL||headB==NULL ) return nullptr; //特殊情况，特殊处理
　　　　while ( h_A!=h_B ) //只要两者指向了相同的 东西，就跳出循环
　　　　 {
　　　　       h_A= ( h_A==NULL ? headB:h_A->next ); //指针h_A遍历完了 链表一后，重新指向链表二，继续遍历
　　　　　　h_B= ( h_B==NULL ? headA:h_B->next ); //指针h_B遍历完了 链表二后，重新指向链表一，继续遍历
　　　　    }
　　return h_A;
　}
};

运行结果： 

代码执行结果：

我的输入

8
[4,1,8,4,5]
[5,6,1,8,4,5]
2
3

我的答案

Intersected at '8'

预期答案

Intersected at '8'

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

树和图_第1题： 中序遍历二叉树

题目描述：

 

给定一个二叉树，返回它的中序 遍历。

 

举例：

示例:

输入: [1,null,2,3]
   1
    \
     2
    /
   3

输出: [1,3,2]

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

解题思路：如果用递归算法，的确很简单。那如果用迭代算法来做，就要构造一个 栈stack 来，并结合vector容器。（但我用的是前面个方法，哈哈~）

学习心得：树和递归是好兄弟，很多时候，他俩都相辅相成。如果要用迭代的话，就要把“vector”或“stack”

或“queue” 结合起来解决问题。

 

实现：（C++） 

/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
　　public:
　　　　void BL( TreeNode* root,vector<int>& vec)　　 //第二个形参，加个 “&”就与众不同啦！引用嘛，要就在递归的工程中，vec里面储存的东西不变
　　　　 {
　　　　      if( root==NULL ) return ;
　　　　　  BL( root->left,vec);　　　　　　 //中序遍历：先左，再中，最后右。
　　　　　  vec.push_back( root->val);
　　　　　  BL( root->right,vec);
　　　　　  return ;
　　　　     }
　　　　vector<int> inorderTraversal(TreeNode* root)

　　　　 {
　　　　　 vector<int> vec;
　　　　　 BL( root,vec );
　　　　    return vec;
　　　　}
};

 

运行结果：

代码执行结果：

我的输入

[1,null,2,3]

我的答案

[1,3,2]

预期答案

[1,3,2]

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

树和图_第2题：二叉树的锯齿形层次遍历

题目描述：

给定一个二叉树，返回其节点值的锯齿形层次遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

 

举例：

例如：
给定二叉树 [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

返回锯齿形层次遍历如下：

[
  [3],
  [20,9],
  [15,7]
]

解题思路：主要是灵活运用 队列，这里还要用到 “双端队列deque”。锯齿形层次的构建，就依靠 “双端队列deque”的特点，要么从队列前端压入，要么从队列后端压入。

学习心得：今天刷力扣，最大的收获就是，新学习到这个C++标准模板库“双端队列deque”。还有

指针在树的遍历操作中的灵活运用。

 

 

实现：（C++）

/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
　　public:
　　　　vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
　　　　queue<TreeNode*> q; 　　　　 //构建一个 queue属性的储存TreeNode*类型数据 的对象
　　　　deque<int> deq;　　　　　　    //构建一个“双端队列” 储存每一层的int类型的数据
　　　　vector<vector<int>> res; 　　　 //最终要返回的 二维vector容器
　　　　if( root==NULL ) return res; 　　 //特殊情况，特殊处理
　　　　int i,n,flag=0;　　　　　　　　 //flag作为一个 判断左右方向放入 的标记
　　　　q.push(root); 　　　　　　　　 //先把“树根”放入队列
　　　　TreeNode *fp;　　　　　　　　 //定义一个移动指针
　　　　while( !q.empty() )　　　　　　 //只要队列里还有元素，说明 还没遍历完
　　　　  {
　　　　       n=q.size();　　　　　　　 //n是每一层装入数据的个数
　　　　　　for( i=0;i<n;i++ )
　　　　　　 {
　　　　　　    fp=q.front();
　　　　　　    q.pop();
　　　　　　　if( flag%2==0 )　　　　 //如果是奇数层，从左至右放入
　　　　　　　     deq.push_back( fp->val );
　　　　　　　else　　　　　　　　 //如果是偶数层，从右至左放入
　　　　　　　　 deq.push_front( fp->val);
　　　　　　   if( fp->left ) 　　　　　　 //这里建议 作一作图，就清晰明了了。 每次都是 从左至右装入。
　　　　　　　　q.push( fp->left );
　　　　　　　if( fp->right )
　　　　　　　　q.push( fp->right );
　　　　　　  }
　　　　　　flag++;
　　　　res.push_back( vector<int>( deq.begin(),deq.end() ) ); 　　 //①新学到了，另一种将数据放入 vector里的方法
　　　　deq.clear(); 　　　　　　　　　　　　　　　　　　　　 //②这里用到了 map库里的 clear()函数。功能：删除所有元素。
　　　}
　　return res;
　　}
};

运行结果：

代码执行结果：

我的输入

[3,9,20,null,null,15,7]

我的答案

[[3],[20,9],[15,7]]

预期答案

[[3],[20,9],[15,7]]

 

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

树和图_第3题： 从前序与中序遍历序列构造二叉树

题目描述：

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

举例：

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]

返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7

解题思路：前序遍历数组的第一个元素一定是根结点，用 hashmap 记录下来。 在中序遍历数组里找到 与前序遍历数组的根结点 值相同的 元素。则该元素的 左边即为 左子树，其右边 即为右子树。

然后进行递归， 把前面句话里的 左子树和右子树 分别重新 “整” 一遍，不停地递归。 结合指针（其实是坐标）来解决。 

学习心得：递归，递归，最难地地方就在于 ①找到递归点。②递归的东西怎么表示。这道题考得很综合。

让我再一次感受到哈希表的强大功能。而且还有一个小小的 小细节（我亲自检验）。就是在转参过程中，

“ vector<int> & preorder”和“vector<int> preorder”是有很大，很大的区别的！虽然两种情况，都能

得到最终的答案。但有“&”（即引用）的情况，其内存消耗将近第二种的 1/10 ！消耗时间也大大缩小！

可见，“& 引用”的功能 还是不容小觑。

 

实现：（C++）

/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
　　private:
　　　　unordered_map<int,int> index; //定义一个私有成员，哈希表。key为int类型，val也是int类型
　　public:
　　　　TreeNode* Tree( const vector<int>& preorder,const vector<int>& inorder,int pre_left,int pre_right,int in_left,int in_right) 　 // 这里的两个 “&” 引用，可以减少很多很多空间！const 有没有无关紧要
　　　　  {
　　　　　  if( pre_left>pre_right ) return nullptr; 　　　　　　　　　 //终止条件
　　　　　  int pre_root_index=pre_left; 　　　　　　　　　　　　 //前序根结点的下标 即是 最左端（或左子树的最左端）的下标
　　　　　  int in_root_index=index[ preorder[pre_root_index] ];　　　　　　　　　　　 //在中序数组中找到 与前序数组中根结点值相等的 元素的下标
　　　　　  int left_tree_size=in_root_index - in_left;　　　　　　　　　　　　　　　　//left_tree_size表示 中序数组中左子树的长度（和前序数组的左子树长度一样的）
　　　　　  TreeNode *root_1=new TreeNode( preorder[pre_root_index] );　　　　　　 //申请一个新的结点
　　　　　  root_1->left=Tree( preorder,inorder,pre_left+1,left_tree_size+pre_left,in_left,in_root_index-1); 　　　　　　 //要解释好这一句话，不轻松啊
　　　　　　　　　　　　　　　//左子树递归。 前序数组的左边界、右边界相应在变；中序数组的左边界、右边界也相应在变。 关键是前序数组中 左子树的长度 和 中序数组中 左子树的长度是相同的。
　　　　　  root_1->right=Tree( preorder,inorder,left_tree_size+pre_left+1,pre_right,in_root_index+1,in_right); 　　　　 //右子树递归。（和左子树递归功能相似）
　　　　      return root_1;
　　　　　 }
　　　　TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
　　　　int i,n=preorder.size();
　　　　for( i=0;i<n;i++ )　　　　　　 //将中序数组中 每个元素(key)，对应到不同的(val)
　　　　    index[ inorder[i] ]=i;
　　return Tree( preorder,inorder,0,n-1,0,n-1 );;
　 }
};

运行结果：

代码执行结果：

我的输入

[3,9,20,15,7]
[9,3,15,20,7]

我的答案

[3,9,20,null,null,15,7]

预期答案

[3,9,20,null,null,15,7]