力扣_初级算法_树_4~5题_和_排序和搜索_2题_和动态规划_1~4题

C++小白所作...单纯记录一下自己刷力扣的学习心得

 

树_第4题：二叉树的层序遍历

题目描述:

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

举例：

示例：
二叉树：[3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

返回其层次遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

学习心得：提升了自己对“队列”的运用能力，提升了对“出队”、“入队”的操作能力。

解题思路：建立一个“队列”，来储存“树”上的数，依次从上到下，从左到右。“出队人数” 由 for循环 控制。另外还要

建立一个二维 “vector容器” 来储存结果，也是“队列”中 “出队的人” 的归属地。

实现：（C++）  

 

/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int> > res; 　　　　　　 //res：result的缩写，结果的意思
if( root==NULL ) return res; 　　　　 //这里res是空的二维容器
queue<TreeNode*> q; 　　　　　　 //定义一个“树结构指针”类型具有队列属性的 变量
q.push(root); 　　　　　　　　　　 //树根放进去
while( !q.empty() ) 　　　　　　　　 //队列不为空时
{
int current_q_size=q.size(); 　　　　 //计算出当且队列的元素个数
res.push_back( vector<int>() );　　 //在res（二维容器）末尾处生成一个“空行”（空的一维容器）
for( int i=0;i<current_q_size;i++ )　　 //用for循环控制“出队人数”
{
auto node=q.front();　　　　　　　　 /*①新学到auto， 知识补充:使用auto定义变量时必须对其进行初始化，在编译阶段编译器需要根据初始化表达式来推导auto的 实际类型。

　　　　　　　　　　　　　　　　　　因此auto并非是一种“类型”的声明，而是一个类型声明时的“占位符”，编译器在编译期会将auto替换为变量实际的 类型。*/
q.pop();
res.back().push_back( node->val ); 　　 //在“二维容器” res里 的最后一行 的最后一位放入node储存的数据
if( node->left ) q.push( node->left ); 　　 //如果该节点有“左孩子”，则放进队列
if( node->right ) q.push( node->right ); 　　 //如果该节点有“右孩子”，则放进队列
}
}
return res;
}
};

 

------------------------------------------------------------------------------------------------------------------------------------

树_第5题：将有序数组转换为二叉搜索树

题目描述：

 

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

 

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

举例：

示例:

给定有序数组: [-10,-3,0,5,9],

一个可能的答案是：[0,-3,9,-10,null,5]，它可以表示下面这个高度平衡二叉搜索树：

      0
     / \
   -3   9
   /   /
 -10  5

学习心得（摘自CSDN，ID：明明是悟空）：采用平衡二叉树的优点是：使树的结构较好，从而提高查找运算的速度。
缺点是：是插入和删除运算变得复杂化，从而降低了他们的运算速度。
解题思路：类似于，把一个有序的数组的 中间 “dia”（吊）起来。 然后采用递归，把“数组中间”的左边的区间 细分，
再把“数组中间”的右边的区间 细分。不断细分，用while( left > right )作为终止条件。
实现：（C++）

/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* helper( vector<int>& nums,int left_index,int right_index )
{
if( left_index > right_index) return nullptr; 　　　　　　 //终止条件
int mid=( left_index+right_index )/2;　　　　　　　　 　 //选择数组中间 靠左边一位的下标（数组元素个数为偶数情况），否则是选择数组中中间间元素的下标(数组元素个数为奇数的情况)
TreeNode* root=new TreeNode(nums[mid]);　　　　　 //建立一个 “树结点”，并调用结构体的构造函数
root->left=helper( nums,left_index,mid-1 ); 　　　　　　 //递归调用，不停细分 数组中间一刀切下来 左边的部分，注意 左右区间范围的变化
root->right=helper( nums,mid+1,right_index );　　　　 //递归调用，不停细分 数组中间一刀切下来 右边的部分，注意 左右区间范围的变化
return root;
}
TreeNode* sortedArrayToBST(vector<int>& nums) {
TreeNode* root=nullptr;
root=helper( nums,0, nums.size()-1 ); 　　　　　　 //区间是 “数组下标”的范围, 准备放入helper函数里面去 “切” 
return root;
}
};

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

排序和搜索_第2题：第一个错误的版本
题目描述：

你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。

假设你有 n 个版本 [1, 2, ..., n]，你想找出导致之后所有版本出错的第一个错误的版本。

你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

举例：

 

 

示例:

 

给定 n = 5，并且 version = 4 是第一个错误的版本。

调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true

所以，4 是第一个错误的版本。

学习心得（）：如果用最直接的“暴力解法”（直接遍历），那会超时。后来学习到“二分法”。
并且不能用“(min+max)/2”来中分，要考虑用“min+(max-min)/2”来中分，以避免超出int能表示的范围。

 

解题思路：不停“二分”，关键是在终止条件那里。无论如何中分，总有一个min和max（ 两者值不同，而且 最少两者的值差1 ）。所以当两者只相差1时

进行 if 判断。

实现：（C++）

 

// The API isBadVersion is defined for you.
// bool isBadVersion(int version);

 

class Solution {
public:
int dichotomy( int min,int max )　　　　　　 //注：dichotomy的中文意思是：二分法
{
if( min==max-1 )
{
if( isBadVersion( min ) )
return min;
else
return max;
}
if( isBadVersion( min+(max-min)/2 ) )
{
return dichotomy( min,min+(max-min)/2 ); 　　 //“二分”左边的部分
}
else
{
return dichotomy( min+(max-min)/2,max);　　 //“二分”左边的部分
}
}
int firstBadVersion(int n) {
if( n==1 ) return 1; 　　　　　　　　 //n=1是单独“拉”出来
return dichotomy( 1,n );
}
};

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

动态规划_第1题：爬楼梯

题目描述：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

举例：

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

学习心得：刚开始想到用高中学到的排列组合，但感觉好麻烦。后面分别列出1、2、3、4、5...阶的情况
渐渐发现规律，发现和 斐波那契【fěi bō nà qì】数列一个样儿。那就不用说了，直接开解。但值得我
回味的是这道题的“数学思想”，渐渐感受到“数学思维”在解某些题的重要性。

解题思路：斐波那契数列，生兔子那个数列，OK~
实现：（C++）

class Solution {
public:
int climbStairs(int n) {
if( n==1 ) return 1; 　　 //一个初始值
if( n==2 ) return 2; 　　 //另一个初始值
int a=1,b=2;
int res,i;
for( i=2;i<n;i++ )
{
res=a+b;
a=b;
b=res;
}
return res;
}
};

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

动态规划_第2题：买卖股票的最佳时机

题目描述：

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票一次），设计一个算法来计算你所能获取的最大利润。

注意：你不能在买入股票前卖出股票。

举例：

示例 1:

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

解题思路：灵活运用 min( 数据值, 数据值 ) 和 max( 数据值, 数据值 ) 两个函数。 取一个类似 “指针” 功能的 int 型变量，

用来储存数组中值最小的 元素。还取 一个 int型的 总利润变量，用max()函数，不停比较，并取最大的那个。

学习心得：算法思维真的很重要。没用“min()”和"max()"之前，硬是怎么想也想不出来。

其实“min()”或“max()”两个函数都可以转变成 if()语句的 判断形式。最主要的还是那个“思维”。

一种状态，买这个股票，买了就“持有”，其后面的状态也是“持有”；不买就是后面的状态都

是“不持有”，也就是说，后面的状态由，前面的状态决定。

实现：（C++）

 

class Solution {
public:
int maxProfit(vector<int>& prices) {
if( prices.size()==0 ) return 0; 　　　　　 //特殊数据，特殊处理
int maxprices,minprices,i;
maxprices=0;
minprices=INT_MAX;　　　　　　　　　　 //INT_MAX：int类型的最大值
for( i=0;i<prices.size();i++ )
{
minprices=min( minprices,prices[i] );
maxprices=max( maxprices,prices[i]-minprices ); 　　 //在 “prices[i]-minprices” 中，minprices是前面最小的一个“股票价格”
}
return maxprices;
}
};

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

动态规划_第3题：最大子序和

题目描述：

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

举例：

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

解题思路：和上一题有相似之处，有异曲同工之妙，只不过这里是  连着“买” 。灵活运用 max() 函数。

学习心得：真的是，脑袋里想清楚了，写代码就快。没有那个“思维”真的 难顶。但不管怎么说

max_result 始终 要把 自身 和 另外一个数据值进行比较。

 实现：（C++）

class Solution {
public:
int maxSubArray(vector<int>& nums) {
if( nums.size()==0 ) return 0; 　　　　　　 //特殊情况，特殊处理
if( nums.size()==1 )         　　　　　　　　 //特殊情况，特殊处理
return nums[0];
int max_res=nums[0],cur_ptr=nums[0],i;　　 //羊毛出在羊身上啊! max_res:最大利润。cur_ptr:当前储存的利润。它俩都先赋初始值nums[0]。
for( i=1;i<nums.size();i++ )
{
cur_ptr=max( nums[i],cur_ptr+nums[i] );　　 //就是这句和下一句要好生理解。cur_ptr:当前储存的利润（可能不是最大利润）
max_res=max( max_res,cur_ptr);　　　　 //先前在 解题思路 里说了，max_res始终要把 自身 和 另外一个数据值进行比较
}
return max_res;
}
};

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

动态规划_第4题：打家劫舍

题目描述：

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

举例：

示例 1：

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。

示例 2：

输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
     偷窃到的最高金额 = 2 + 9 + 1 = 12 。

 

提示：

• 0 <= nums.length <= 100
• 0 <= nums[i] <= 400

解题思路：先把数学公式列出来（这步很关键，图来源于力扣官方）。然后找最基础的初始条件值。采用递归解出。

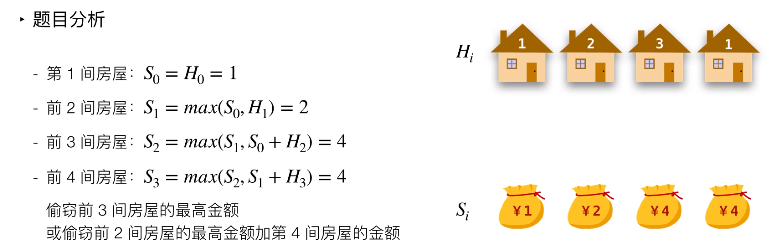
学习心得：通过做这道题，我是深刻第认识到 “数学” 的重要性，这道题里面就用到了“数列的项”

和“数列的和”的知识。把递归的本色用的淋漓尽致。

实现：（C++）

class Solution {
public:
int rob(vector<int>& nums) {
if( nums.size()==0 ) return 0;　　　　　　 //特殊情况，特殊处理
if( nums.size()==1 ) return nums[0]; 　　 //特殊情况，特殊处理
vector<int> v(nums.size(),0); 　　　　 //建立一个一维的“vector容器” 大小是 “nums容器” 的大小，且其内全部赋值为0
v[0]=nums[0];　　　　　　　　　　 //一个初始条件值
v[1]=max(nums[0],nums[1]); 　　　　 //另一个初始条件值
int i=2; 　　　　　　　　　　　　 //从第三家开始偷（前提是要有三家或三家以上的房子）
while( i <nums.size() )
{
v[i]=max( v[i-2]+nums[i],v[i-1] ); 　　　　 //递归，出现了！就是那个数学公式
i++;
}
return v[ nums.size()-1 ];
}
};