Convolutional 2D Knowledge Graph Embeddings

https://ojs.aaai.org/index.php/AAAI/article/view/11573

---

Abstract Link prediction for knowledge graphs is the task of predicting missing relationships between entities. Previous work on link prediction has focused on shallow, fast models which can scale to large knowledge graphs. However, these models learn less expressive features than deep, multi-layer models which potentially limits performance. (之前模型浅层、快速但表现力差不及深层模型). In this work we introduce ConvE, a multi-layer convolutional network model for link prediction, and report state-of-the-art results for several established datasets. We also show that the model is highly parameter efficient, yielding the same performance as DistMult and R-GCN with 8x and 17x fewer parameters. Analysis of our model suggests that it is particularly effective at modelling nodes with high indegree – which are common in highlyconnected, complex knowledge graphs such as Freebase and YAGO3. In addition, it has been noted that the WN18 and FB15k datasets suffer from test set leakage, due to inverse relations from the training set being present in the test set however, the extent of this issue has so far not been quantified. We find this problem to be severe: a simple rule-based model can achieve state-of-the-art results on both WN18 and FB15k. To ensure that models are evaluated on datasets where simply exploiting inverse relations cannot yield competitive results, we investigate and validate several commonly used datasets – deriving robust variants where necessary. We then perform experiments on these robust datasets for our own and several previously proposed models, and find that ConvE achieves state-of-the-art Mean Reciprocal Rank across all datasets.

1. Introduction

之前提出的模型如disMult，Trans等，都是浅层模型，模型比较简单，参数较少、训练速度快，但是这些模型相比于深层模型，表现力差，不能抓到更复杂的信息。

浅层模型想要增加特征数量的方法，只能是增加embedding的维度，但随着知识图谱的不断扩大，模型参数会变得很大，也很容易过拟合。

本文的贡献：

• 介绍了一个简单的、有竞争力的2D卷积链路预测模型，ConvE；
• 开发了一个1-N的评分程序，加速三倍的训练和300倍的评估；
• 更好的参数效率，比DistMult和R-GCN在FB15k-237表现更好，参数却是它们的1/8,1/17；
• 论文提出的模型与其他浅的模型的性能区别随着知识图谱复杂度的增加而成比例增加
• 验证了测试数据集泄露的严重性，同时提出了一个改进版的数据集
• 对ConvE和先前其他最好的模型做了评估，ConvE取得了SOTA效果

1D vs 2D Convolutions

文章认为2D卷积比1D卷积通过embedding之间的交互增强了模型的表现力。
1D卷积对一维的embedding，通过k=3的过滤器进行卷积，这样只能捕捉到两个向量拼接点处的交互：

\[\left( \left[ \begin{matrix} a & a & a \\ \end{matrix} \right];\left[ \begin{matrix} b & b & b \\ \end{matrix} \right] \right)=\left[ \begin{matrix} a & a & a & b & b & b \\ \end{matrix} \right]\]

得到的结果维度为1*4。

2D卷积将二维embedding进行堆叠，然后用3*3的卷积核进行卷积，这样可以捕捉整个拼接行的交互：

\[\left( \left[ \begin{matrix} a & a & a \\ a & a & a \\ \end{matrix} \right];\left[ \begin{matrix} b & b & b \\ b & b & b \\ \end{matrix} \right] \right)=\left[ \begin{matrix} a & a & a \\ a & a & a \\ b & b & b \\ b & b & b \\ \end{matrix} \right]\]

得到的结果维度为2*1，也可以采用以下形式进行堆叠：

\[\left[ \begin{matrix} a & a & a \\ b & b & b \\ a & a & a \\ b & b & b \\ \end{matrix} \right]\]

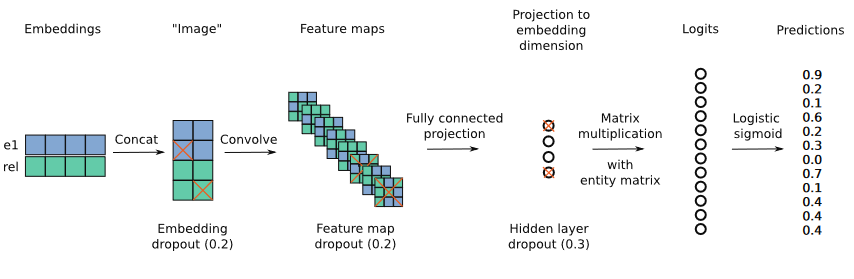
Remark1： nn.Conv2d(1, 32, (3, 3), bias=True)

ConvE的打分函数：

\[{{\psi }_{r}}\left( {{e}_{s}},{{e}_{o}} \right)=f\left( vec\left( f\left( \left[ {{{\bar{e}}}_{s}};{{{\bar{r}}}_{r}} \right]*\omega \right) \right)W \right){{e}_{o}}\tag{1} \]

\({e}_{s}\),\({e}_{o}\)表示头部实体和尾部实体的embedding，\({{{\bar{e}}}_{s}},{{{\bar{r}}}_{r}}\)代表Reshape后的头部实体和关系向量，\(\omega\)代表卷积核，\(W\)代表投影矩阵。

交叉熵损失：

\[\mathcal{L}\left( p,t \right)=-\frac{1}{N}\sum\limits_{i}{\left( {{t}_{i}}\cdot \log \left( {{p}_{i}} \right)+\left( 1-{{t}_{i}} \right)\cdot \log \left( 1-{{p}_{i}} \right) \right)}\tag{2} \]