20181102 T2 求和

给定长度为𝑛的序列𝑎，定义一次操作为：
1. 定义序列𝑆（序列𝑎的前缀和）
2. 将𝑆复制回𝑎。
给定整数𝑘，求对𝑎进行𝑘次操作后每个元素的值。

---

 

很好的一道数学题，考场上没有想出来，连暴力都没有写对QAQ

首先来看暴力，直接去维护，有30

然后来看满分做法

首先，很明确的就是，我们可以算出每一项的系数，我在考场上就有了这个想法，但是来不及推导了

先举一个例子

1 0 0 0 0

进行五次操作

会形成一个矩阵：
1 1 1 1 1

1 2 3 4 5

1 3 6 10 15

1 4 10 20 35 

1 5 15 35 70

然后就发现长得极其的像杨辉三角

而我们又知道，杨辉三角每一项的值是可以用组合数来求的

也就是C（n-1,m-1），n代表第n行，m代表第m列

而这里的系数在杨辉三角中是斜着的一列

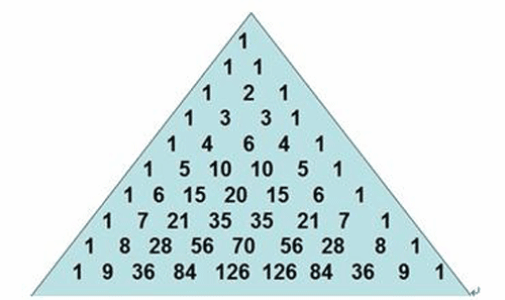
因为有了求系数的方法

现在我们的目标就转化为了预处理出组合数然后直接计算结果

我们还有一个结论就是C（n,m）=C(n-1,m-2)/(n-2)*n

以及组合数的对称，会变化的也只有n的值

递推的方式就出来了

但好似很显然，直接算的话会爆long long

所以要在计算过程中qui逆元来应对除法

最后直接暴力求出结果并且输出即可

注：求得过程中，前面的数的系数更大，所以要在开一个循环来从后往前相乘，时间复杂度O（n^2）

下面给出代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#define ll long long
using namespace std;
const ll M=1000000007;
inline ll rd(){
    ll x=0,f=1;
    char ch=getchar();
    for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
    for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
    return x*f;
}
inline void write(ll x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
    return ;
}
ll a[100006];
ll n,k;
ll INV[100006];
ll pow(ll a,ll b){
    ll ans=1,base=a;
    while(b){ if(b&1){ans*=base,ans%=M;} base*=base,base%=M,b>>=1;}
    return ans;
}
ll inv(ll x,ll y){return (x*pow(y,M-2))%M;}
int main(){
    freopen("sum.in","r",stdin);
    freopen("sum.out","w",stdout);
    n=rd(),k=rd(),INV[0]=1;
    for(ll i=1;i<=n;i++) INV[i]=(inv(INV[i-1],i)*(i+k-1))%M;
    for(ll i=1;i<=n;i++){
        ll ans=0;
        a[i]=rd();
        for(ll j=i;j>=1;j--) ans=(ans+(a[j]*INV[i-j])%M)%M;
        write(ans),putchar(' ');
    }
    return 0;
}