Poj3177 分离的路径

为了从 F 个草场中的一个走到另一个，贝茜和她的同伴们不得不路过一些她们讨厌的可怕的树。奶牛们已经厌倦了被迫走某一条路，所以她们想建一些新路，使每一对草场之间都会至少有两条相互分离的路径，这样她们就有多一些选择。
每对草场之间已经有至少一条路径，给出所有 R 条双向路的描述，每条路连接了两个不同的草场，请计算最少的新建道路的数量。
路径由若干道路首尾相连而成，两条路径相互分离，是指两条路径没有一条重合的道路，但是两条分离的路径上可以有一些相同的草场。

对于同一对草场之间，可能已经有两条不同的道路，你也可以在它们之间再建一条道路，作为另一条不同的道路。

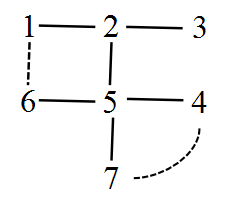
样例解释

图中实线表示已有的道路，虚线表示新建的两条道路。现在可以检验一些路径，比如：

草场 1 和草场 2：
1→2 和1→6→5→2
草场 1 和草场 4：
1→2→3→4 和 1→6→5→4
草场 3 和草场 7：
3→4→7 和3→2→5→7
事实上，每一对草场之间都连接了两条分离的路径。

 

---

题目描述就表明了是显然的点双联通分量

然后缩点之后根据定义来计算

一个图缩点之后会变成一棵树，而让一棵树点双联通，最少情况就是入度为一的点的个数除2向上取整

下面给出代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
using namespace std;
inline int rd(){
    int x=0,f=1;
    char ch=getchar();
    for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
    for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
    return x*f;
}
inline void write(int x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
    return ;
}
int n,m;
int head[1000006],nxt[1000006],to[1000006];
int v[1000006];
int total=0;
void add(int x,int y){
    total++;
    to[total]=y;
    nxt[total]=head[x];
    head[x]=total;
    return ;
}
int dfn[1000006],low[1000006];
int tot=0;
int book[1000006];
int set=0;
int sta[1000006];
int color[1000006];
int cnt=0;
int v2[1000006];
int f[100006];
void tarjan(int x,int fa){
    low[x]=dfn[x]=++tot;
    sta[++set]=x;
    f[x]=fa;
    book[x]=1;
    for(int e=head[x];e;e=nxt[e]){
        if(to[e]==fa) continue;
        if(!dfn[to[e]]){
            tarjan(to[e],x);
            low[x]=min(low[x],low[to[e]]);
        }
        else if(book[to[e]]) low[x]=min(low[x],dfn[to[e]]);
    }
    if(dfn[x]==low[x]){
        book[x]=0;
        cnt++;
        color[x]=cnt;
        v2[cnt]=v[x];
        while(set&&sta[set]!=x){
            int h=sta[set];
            book[h]=0;
            color[h]=cnt;
            v2[cnt]+=v[h];
            set--;
        }
        set--;
    }
    return ;
}
int du[100006];
int main(){
    n=rd(),m=rd();
    for(int i=1;i<=m;i++){
        int x=rd(),y=rd();
        add(x,y),add(y,x);
    }
    for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,i);
    for(int i=1;i<=n;i++) if(color[i]!=color[f[i]]) du[color[i]]++,du[color[f[i]]]++;
    int ans=0;
    for(int i=1;i<=cnt;i++) if(du[i]==1) ans++;
    write((ans+1)/2);
    return 0;
}