POJ1691平板涂色

题目描述

原题来自：POJ 1691

CE 数码公司开发了一种名为自动涂色机（APM）的产品。它能用预定的颜色给一块由不同尺寸且互不覆盖的矩形构成的平板涂色。

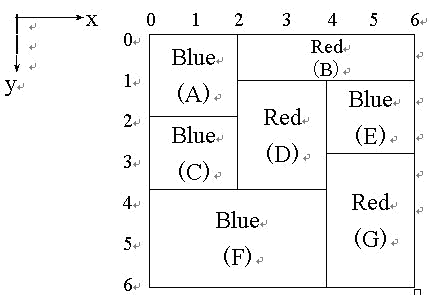
为了涂色，APM 需要使用一组刷子。每个刷子蘸了颜色 C 。APM 拿起一把蘸有颜色 C 的刷子，并给所有颜色为 C 的矩形涂色。请注意，涂色有顺序要求：为了避免颜料渗漏使颜色混合，一个矩形只能在所有紧靠它上方的矩形涂色后，才能涂色。例如图中矩形 F 必须在 C 和 DDD 涂色后才能涂色。注意，每一个矩形必须立刻涂满，不能只涂一部分。

写一个程序求一个使 APM 拿起刷子次数最少的涂色方案。注意，如果一把刷子被拿起超过一次，则每一次都必须记入总数中。

输入格式

第一行为矩形的个数 N 。
下面有 N 行描述了 N 个矩形。每个矩形有 555 个整数描述，左上角的 y 坐标和 x 坐标，右下角的 y 坐标和 x 坐标，以及预定颜色。

输出格式

一行一个整数，表示拿起刷子的最少次数。

样例

样例输入

7
0 0 2 2 1
0 2 1 6 2
2 0 4 2 1
1 2 4 4 2
1 4 3 6 1
4 0 6 4 1
3 4 6 6 2

样例输出

3

数据范围与提示

对于全部数据，1≤N≤14，颜色号为 1 到 20 的整数。保证平板的左上角坐标总是 (0,0)，坐标的范围是 0 到 9 。

---

我只想吐槽CE公司这个名字不太吉利

 

这道题比较水，一个简单的DFS就能过，只不过加一点贪心的思想

为了尽量少的拿起刷子，我们在一种颜色可以涂的情况下，一定要尽量多的涂

下面给出代码：

#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
inline int rd(){
    int x=0,f=1;
    char c=getchar();
    for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
    for(;isdigit(c);c=getchar()) x=x*10+c-'0';
    return x*f;
}
inline void write(int x){
     if(x<0) putchar('-'),x=-x;
     if(x>9) write(x/10);
     putchar(x%10+'0');
}
struct node{int sx,sy,ex,ey,co;}s[100000];
bool cmp(const node &x,const node &y){
    if(x.sx!=y.sx) return x.sx<y.sx;
    return x.sy<y.sy;
}
int n,m;
int color[1000],book[1000][1000],used[1000];
int ans=99999;
bool check(int x){//对于一块区域，是否能涂 
    for(int i=1;i<=n;i++) if(book[x][i]&&!used[i]) return 0;
    return 1;
}
void dfs(int step,int sum,int la){//分别是用了几次，涂了几块，和上一个涂的 
    if(step>=ans) return ;
    if(sum==n){
        ans=min(ans,step);
        return ;
    }
    for(int i=1;i<=m;i++){//尽量用同种颜色 
        int cnt=0;
        if(i!=la&&color[i]!=0){
            for(int j=1;j<=n;j++){
                if(used[j]==0&&s[j].co==i&&check(j)==1){//能涂就涂 
                    used[j]=1;
                    cnt++;
                }
                else if(used[j]!=0&&s[j].co==i) used[j]++; 
            }
            if(cnt>0) dfs(step+1,sum+cnt,i);//如果有可以涂色的，就继续搜索 
            for(int j=n;j>=1;j--){
                if(used[j]==1&&s[j].co==i&&check(j)==1){//赋原来的值 
                    used[j]=0;
                    cnt--;
                }
                else if(used[j]>1&&s[j].co==i) used[j]--;
            }
        }
    }
    return ;
}
int main(){
    n=rd();
    int i,j,k;
    for(i=1;i<=n;i++){
        s[i].sx=rd(),s[i].sy=rd(),s[i].ex=rd(),s[i].ey=rd(),s[i].co=rd();
        s[i].sx++;
        s[i].sy++;
        color[s[i].co]++;
    }
    for(i=1;i<=20;i++) if(color[i]) m=i;
    sort(s+1,s+n+1,cmp);//按照需要涂色顺序排列 
    for(i=2;i<=n;i++)
        for(j=i-1;j>=1;j--) 
            if(s[i].sx==s[j].ex+1&&((s[i].sy>=s[j].sy&&s[i].sy<=s[j].ey)||(s[i].ey>=s[j].sy&&s[i].ey<=s[j].ey)))//记录对于排序后的第i个涂色区域有那几个先行条件 
                book[i][j]=1;
    dfs(0,0,0);
    write(ans);
    return 0;
}