浅谈图的割点和割边(Tarjan)
快要NOIP了,想着复习一下图论,然后就发现不太会写割点和割边了,而且之前还没有写过博客,所以今天来填个坑
割点
首先是割点,什么是割点呢
就是在一个连通的无向图中,把一个点去掉之后,图就不再连通,去掉的这个点就是割点
我们来举一个例子:
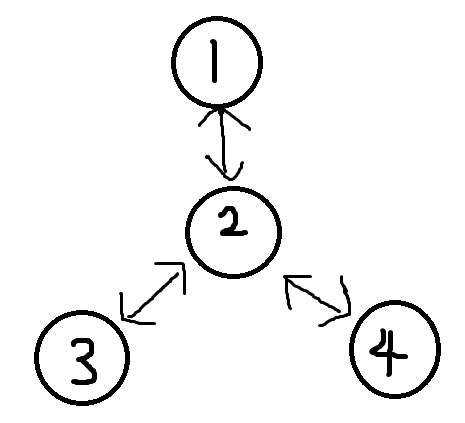
显而易见,上面这个图的割点是2
还有两点要注意的
1.割点可能有很多个
2.无向图和有向图都有割点
然后我们来看一看如何实现割点
方案一:枚举去掉每个点的情况,DFS判断时间复杂度O(n^2)
方案二:Tarjan实现
如果你不会Tarjan,可与去看看我的一篇博客
传送门:https://www.cnblogs.com/WWHHTT/p/9744658.html
好了,现在我们假定大家都已经学会了Tarjan,没学的赶紧去学
其实割点就是在Tarjan的基础上加了几个判断
首先是用一个状态fa来记录当前点的父亲
然后再搜索过程中记录以当前节点为根的子树有多少个
判断一共有两种
(1)当前点是根时,它的子树必须要超过两个,否则不是割点。
至于为什么,我们看上面的图
我们定义1为整个图的根
然后去掉1时
图是这样的:

大家都很和谐,没有了1,照样过的很好(这是我见过根节点被黑的最惨的一次)
(2)当前点不是根时,如果它有一个儿子在不经过它的情况下,不能够回到它的父亲,那么这个点就是割点
举例:
上图我们把2去掉后
是这个样子滴: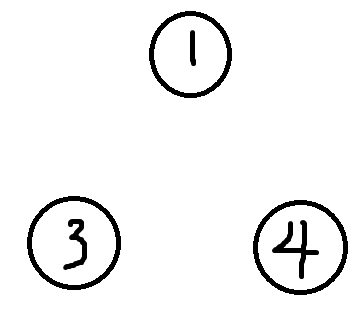
大家都跟对方没了联系(莫名想到春物的是不是没救了)
既然已经明白了规则
下面来看看具体的实现过程吧
还是用刚才的图(方便我画) (红色的点表示当前搜到的节点)
我们从点1开始搜
首先是到了1的唯一的儿子2
然后发现2也有儿子,就继续搜,然后到了3
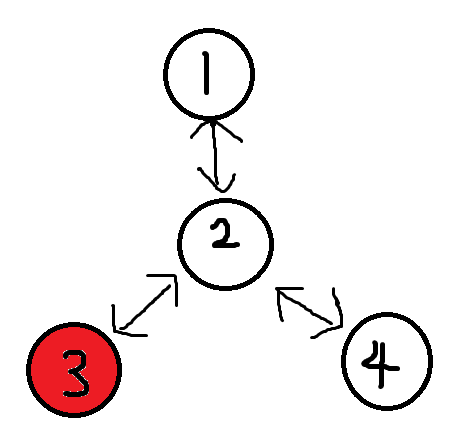
这时我们发现3唯一的连边是2
更新low[3]
此时 DFN[1]=1
LOW[1]=1
DFN[2]=2;
LOW[2]=2;
DFN[3]=3;
LOW[3]=2;
DFN[4]=0;
LOW[4]=0;
因为3没有儿子了,代表low[3]的值已经不会变了,比较low[3]和dfn[2],我们发现,3不经过2无法回到dfs序更更高的点
所以2是割点
然后我们来到了2的第二个儿子4

和3的情况一样,更新loe[4]
此时 DFN[1]=1
LOW[1]=1
DFN[2]=2;
LOW[2]=2;
DFN[3]=3;
LOW[3]=2;
DFN[4]=4;
LOW[4]=2;
4现在也没有儿子了,比较low[4]和dfn[2],判定2为割点,回溯
现在我们又回到了2
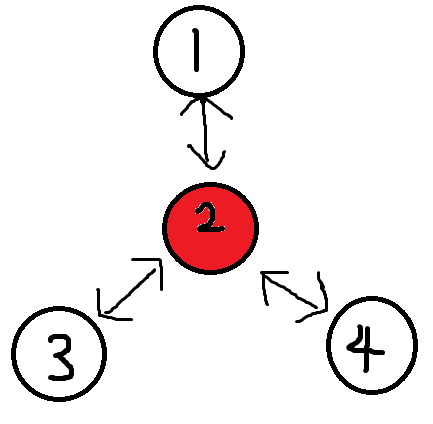
此时除了1(是2父亲),2的儿子已经都跑完了,现在我们已知2有两个子树
但是2不是根节点,所以没用,继续回溯
现在又回到了1
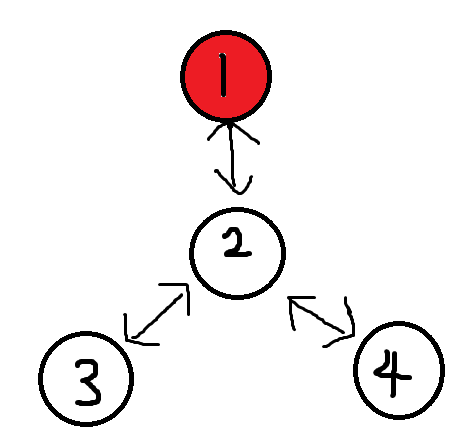
我们得到了1的子树数量为1,就算1是根节点,还是没用(好可怜)
于是割点就跑完了
下面给出一组数据:
第一行n,m,代表有n个点,m条边
之后m行,每行两个数x,y,代表x,y之间有一条无向边
4 3
1 2
2 3
2 4
输出
所有的割点
2
下面给出代码:(有注释哦)
#include<iostream> #include<cmath> #include<cstdio> #include<cstdlib> #include<cstring> #include<string> #include<algorithm> using namespace std; inline int min(int a,int b){return a<b?a:b;} inline int max(int a,int b){return a>b?a:b;} inline int rd(){ int x=0,f=1; char c=getchar(); for(;!isdigit(c);c=getchar()) if(c=='-') f=-1; for(;isdigit(c);c=getchar()) x=x*10+c-'0'; return x*f; } inline void write(int x){ if(x<0) putchar('-'),x=-x; if(x>9) write(x/10); putchar(x%10+'0'); } int n,m; int head[100006]; int nxt[200006],to[200006]; int total=0; void add(int x,int y){ total++; to[total]=y; nxt[total]=head[x]; head[x]=total; return ; } int dfn[100006],low[100006]; int tot=0; int book[100006]; void tarjan(int x,int fa){//记录一个fa,代表当前点的父亲 dfn[x]=low[x]=++tot; int child=0;//以x为根的子树的个数 for(int e=head[x];e;e=nxt[e]){ if(!dfn[to[e]]){ tarjan(to[e],x);//扩展 low[x]=min(low[x],low[to[e]]);//回溯low if(x==fa) child++;//只有在当前点是根时用记录child if(x!=fa&&low[to[e]]>=dfn[x]) book[x]=1;//如果一个点不是根,并且它的儿子在不经过它的情况下无法回到它的父亲,那么它也是割点 } else if(to[e]!=fa) low[x]=min(low[x],dfn[to[e]]);//如果一个点被搜索过了并且是x的儿子或者是它的父亲,就可以直接回溯 } if(x==fa&&child>=2) book[x]=1;//如果一个点是根并且有多于两个子树,就是割点 return ; } int main(){ n=rd(),m=rd(); for(int i=1;i<=m;i++){ int x=rd(),y=rd(); add(x,y);//无向图 add(y,x); } for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,i);//防止图不连通 for(int i=1;i<=n;i++) if(book[i]) printf("%d ",i);//一个图可能有多个割点 return 0; }
割边
我们来看看割边
割边呢,也称作桥,和个点很像,指的是在一个图中,去掉某一条边后,这个图不联通了
举个例子:
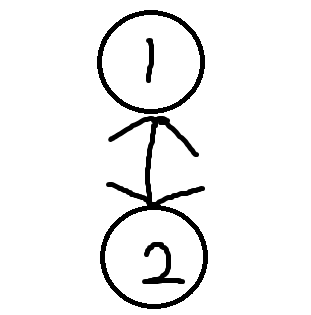
上面这个图,把中间的边去掉之后,1和2就不连通了,所以边1->2就是割边
具体的实现也和割点类似
只不过少一种判断而已
割边是非常好判断的,因为不存在根之类的东西
一条边是不是割边只需要判断这条边连接的两个节点是否可以从其他的路径连通
我们再举一个例子: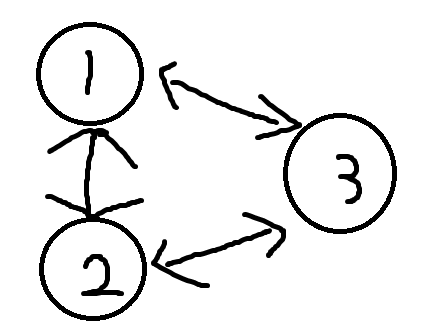
在刚才的图上增加一个点3,分别连接1,2
此时我们去掉1->2
仍然有一条路径可以从2到达1,所以1->就不是割边了
具体的实现过程就不呈现了(反正就算这样也没有比我写得更详细的了)
上组数据吧
和之前的规定一样
2 1
1 2
输出
1->2
下面给出代码:
#include<iostream> #include<cmath> #include<cstdio> #include<cstdlib> #include<cstring> #include<string> #include<algorithm> using namespace std; inline int min(int a,int b){return a<b?a:b;} inline int max(int a,int b){return a>b?a:b;} inline int rd(){ int x=0,f=1; char c=getchar(); for(;!isdigit(c);c=getchar()) if(c=='-') f=-1; for(;isdigit(c);c=getchar()) x=x*10+c-'0'; return x*f; } inline void write(int x){ if(x<0) putchar('-'),x=-x; if(x>9) write(x/10); putchar(x%10+'0'); } int n,m; int head[100006]; int nxt[200006],to[200006]; int total=0; void add(int x,int y){ total++; to[total]=y; nxt[total]=head[x]; head[x]=total; return ; } int dfn[100006],low[100006]; int tot=0; void tarjan(int x,int fa){ dfn[x]=low[x]=++tot; for(int e=head[x];e;e=nxt[e]){ if(!dfn[to[e]]){ tarjan(to[e],x);//扩展 low[x]=min(low[x],low[to[e]]);//回溯low if(low[to[e]]>dfn[x]) printf("%d->%d\n",x,to[e]);//如果两点之间只有这一条路径,那么它是割边 } else if(to[e]!=fa) low[x]=min(low[x],dfn[to[e]]);//如果一个点被搜索过了并且是x的儿子或者是它的父亲,就可以直接回溯 } return ; } int main(){ n=rd(),m=rd(); for(int i=1;i<=m;i++){ int x=rd(),y=rd(); add(x,y);//无向图 add(y,x); } for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,i); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号