二分的弟弟“三分”

相信大家一定都学过二分算法，没学过的GUN回去重学。

那么今天来学习一下他的弟弟，三分。

三分法适用于求凸型函数的鸡汁极值。不知道函数是什么的可以洗洗睡了先好好学习数学。

而二次函数就是一个典型的例子。

如图所示

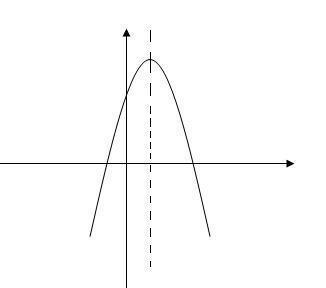
三分所求的，就是这个二次函数与图中虚线的交点的函数值。

那么怎样求这个值呢，二分法显然是不行的，因为这个函数不具备单调性(并且有时精度不够)，所以二分法的兄弟算法“三分”也就诞生了，DUANG DUANG DUANG  

首先，我们设当前的求解区间为[ L , R ]，看起来与二分完全一样极其相似，但是它既然叫做“三分”那么聪明的小朋友肯定已经知道了，我们要将这段区间均分成三份。

我们需要两个mid来存点

m1=L+(R-L)/3

m2=R-(R-L)/3 或者 L+(R-L)/3*2

如图所示

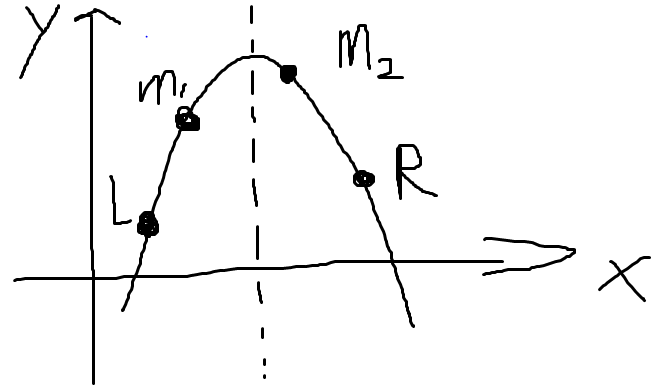
接下来我们计算这两个点的函数值 f(m1) ， f(m2)  。

比较这两个函数值的大小，我们称函数值更大的那个点m2为好点（仅适用于样例，求最大值或最小值由题目来定）。

根据好人必须死法则，他成功的没有存活下来。

而另一个点“坏点”m1则凭借顽强的小强精神活了下来。

因为最优点必定更靠近好点，否则他就不是好点了。

 

我们可以推出，最优点一定在m1 和 R 之间。

此时，我们的求解区间从[ L , R ] ，变成了 [ m1 , R ]。

如图

 

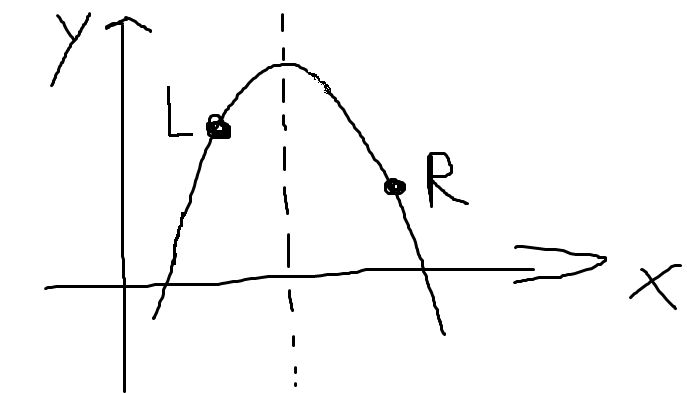
以此类推，根据最终的终止条件，我们可以求出函数的极值的近似值（必须定一个精度）（不排除有精确值）。

 代码如下

#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
inline int min(int a,int b){return a<b?a:b;}
inline int max(int a,int b){return a>b?a:b;}
inline int rd()
{
    int x=0,f=1;
    char c=getchar();
    for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
    for(;isdigit(c);c=getchar()) x=x*10+c-'0';
    return x*f;
}
inline void write(long long x)
{
     if(x<0) putchar('-'),x=-x;
     if(x>9) write(x/10);
     putchar(x%10+'0');
}
double a,b,c;
double f(double x){return x*x*a+x*b+c;}//求函数值 
int main()
{
    cin>>a>>b>>c;//函数 
    double l=1e-9,r=1e9;//初始求解区间  根据题目定义 
    while(r-l>=1e-11)//终止条件 
    {
        double m1=l+(r-l)/3.0;//取三等分点   用.0以防被卡
        double m2=r-(r-l)/3.0;
        if(f(m1)<=f(m2)) l=m1;//判断好点和坏点 修改区间 
        else r=m2;
    }
    cout<<r;//输出结果 有时需要输出函数值或保留小数位数 一定要注意 
    return 0;
}

 

最后喜欢的话不如来推荐，评论，关注三连。

不喜欢的话也昧着良心推荐一下吧！！！！