s - t 平面图最大流 （附例题 bzoj 1001）

以下均移自 周冬的《两极相通-浅析最大最小定理在信息学竞赛中的应用》

平面图性质

1、（欧拉公式）如果一个连通的平面图有n个点，m条边和f个面，那么f=m-n+2

2、每个平面图G都有一个与其对偶的平面图G* G*中的每个点对应G中的一个面

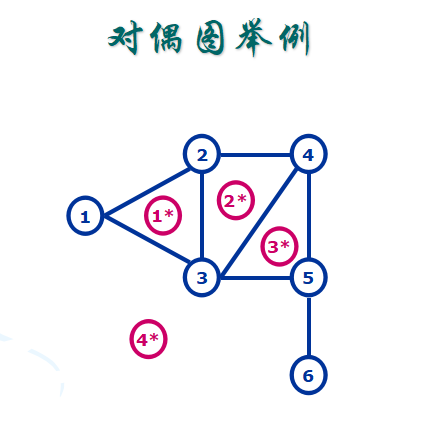
G*中的每个点对应G中的一个面

对于G中的每条边e

e属于两个面f1、f2，加入边(f1*， f2*)

 

 

e只属于一个面f，加入回边(f*， f*)

 

平面图G与其对偶图G*之间存在怎样的关系呢？

G的面数等于G*的点数，G*的点数等于G的面数，

G与G*边数相同 G*中的环对应G中的割一一对应

 

 

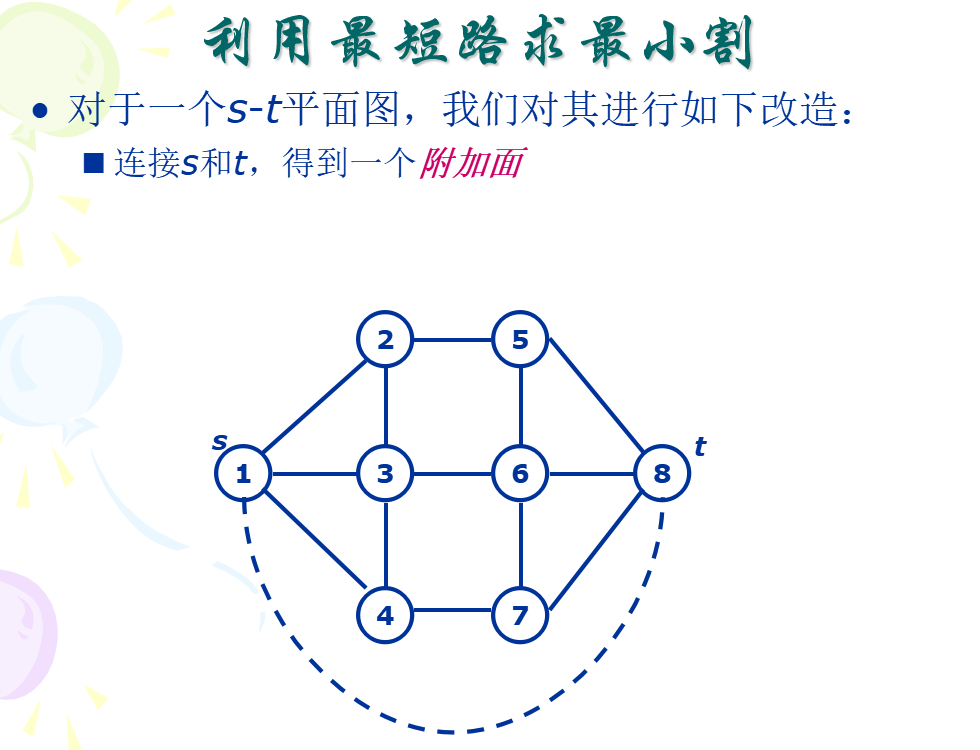
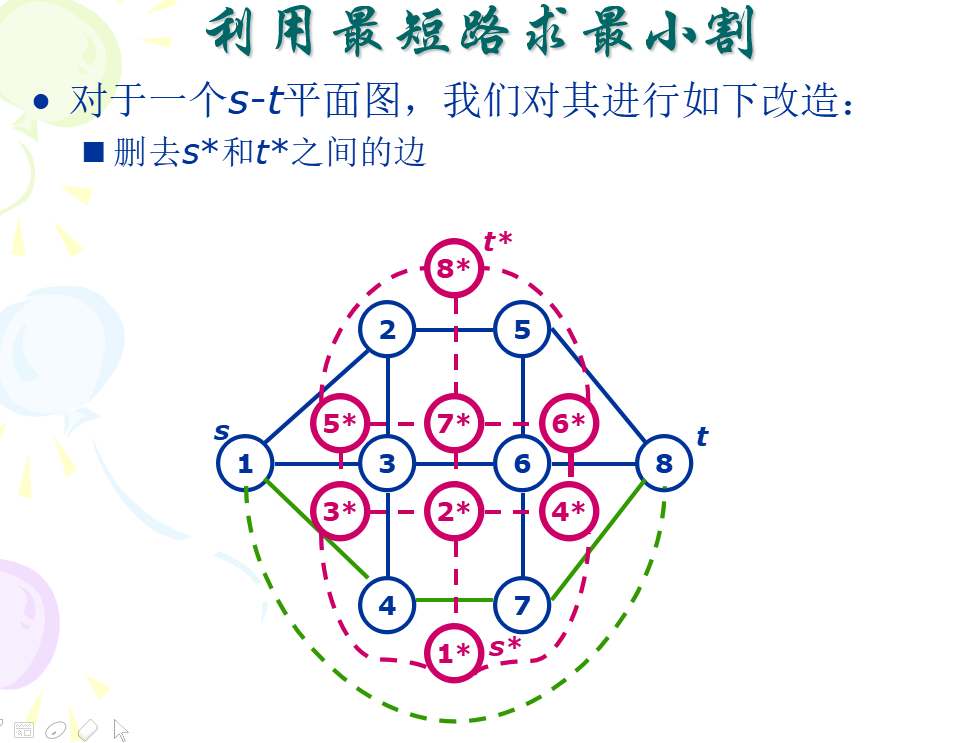
例题：BZOJ 1001 

 

1001: [BeiJing2006]狼抓兔子

Time Limit: 15 Sec  Memory Limit: 162 MB
Submit: 29380  Solved: 7697
[Submit][Status][Discuss]

Description

现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，

而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

 

左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路 

1:(x,y)<==>(x+1,y) 

2:(x,y)<==>(x,y+1) 

3:(x,y)<==>(x+1,y+1) 

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，

开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下解(N,M)的窝中去，狼王开始伏击

这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，

才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的

狼的数量要最小。因为狼还要去找喜羊羊麻烦.

Input

第一行为N,M.表示网格的大小，N,M均小于等于1000.

接下来分三部分

第一部分共N行，每行M-1个数，表示横向道路的权值. 

第二部分共N-1行，每行M个数，表示纵向道路的权值. 

第三部分共N-1行，每行M-1个数，表示斜向道路的权值. 

输入文件保证不超过10M

Output

输出一个整数，表示参与伏击的狼的最小数量.

Sample Input

3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6

Sample Output

14

 

 

解析：

　　根据上文建图

　　   偌。。这就是建出来的图   然后跑一遍spfa就好啦

对啦对啦。。。n == 1 和 m == 1 的时候要单独考虑

 

#include <iostream>
#include <cstdio>
#include <sstream>
#include <cstring>
#include <map>
#include <cctype>
#include <set>
#include <vector>
#include <stack>
#include <queue>
#include <algorithm>
#include <cmath>
#include <bitset>
#define rap(i, a, n) for(int i=a; i<=n; i++)
#define rep(i, a, n) for(int i=a; i<n; i++)
#define lap(i, a, n) for(int i=n; i>=a; i--)
#define lep(i, a, n) for(int i=n; i>a; i--)
#define rd(a) scanf("%d", &a)
#define rlld(a) scanf("%lld", &a)
#define rc(a) scanf("%c", &a)
#define rs(a) scanf("%s", a)
#define pd(a) printf("%d\n", a);
#define plld(a) printf("%lld\n", a);
#define pc(a) printf("%c\n", a);
#define ps(a) printf("%s\n", a);
#define MOD 2018
#define LL long long
#define ULL unsigned long long
#define Pair pair<int, int>
#define mem(a, b) memset(a, b, sizeof(a))
#define _  ios_base::sync_with_stdio(0),cin.tie(0)
//freopen("1.txt", "r", stdin);
using namespace std;
const int maxn = 2001000, INF = 0x7fffffff, LL_INF = 0x7fffffffffffffff;

int head[maxn], cnt, n, m, s, t;
int d[maxn << 1], vis[maxn];
struct node
{
    int u, v, w, next;
}Node[maxn << 2];

void add_(int u, int v, int w)
{
    Node[cnt].u = u;
    Node[cnt].v = v;
    Node[cnt].w = w;
    Node[cnt].next = head[u];
    head[u] = cnt++;
}

void add(int u, int v, int w)
{
    add_(u, v, w);
    add_(v, u, w);
}

bool spfa(int s)
{
    for(int i = 0; i < (maxn << 1); i++) d[i] = INF;
    queue<int> Q;
    mem(vis, 0);
    Q.push(s);
    vis[s] = 1;
    d[s] = 0;
    while(!Q.empty())
    {
        int u = Q.front(); Q.pop();
        vis[u] = 0;
        for(int i = head[u]; i != -1; i = Node[i].next)
        {
            node e = Node[i];
            if(d[e.v] > d[u] + e.w)
            {
                d[e.v] = d[u] + e.w;
                if(!vis[e.v])
                {
                    Q.push(e.v);
                    vis[e.v] = 1;
                }
            }
        }
    }
    return true;
}

void init()
{
    mem(head, -1);
    cnt = 0;
}

int main()
{
    init();
    int u, v, w;
    cin >> n >> m;
    s = 0, t = n * m * 2 + 1;
    if(n == 1){
        int minn = INF;
        for(int i = 0; i < m; i++){
            rd(w);
            minn = min(minn, w);
        }
        pd(minn);
        return 0;
    }
    if(m == 1){
        int minn = INF;
        for(int i = 0; i < n - 1; i++){
            rd(w);
            minn = min(minn, w);
        }
        pd(minn);
        return 0;
    }
    for(int i = 0; i < n; i++)
    {
        for(int j = 1; j <= m - 1; j++)
        {
            cin >> w;
            if(i == 0)
                add(t, i * (m - 1) + j, w);
            else if(i == n - 1)
                add((n - 1) * (m - 1) + (i - 1) * (m - 1) + j, s, w);
            else
                add(i * (m - 1) + j, (n - 1) * (m - 1) + (i - 1) * (m - 1) + j, w);
        }
    }
    for(int i = 0; i < n - 1; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            cin >> w;
            if(j == 1)
                add(s, (n - 1) * (m - 1) + i * (m - 1) + j, w);
            else if(j == m)
                add((i + 1) * (m - 1), t, w);
            else
                add(i * (m - 1) + (j - 1), (n - 1) * (m - 1) + i * (m - 1) + j, w);
        }
    }
    for(int i = 0; i < n - 1; i++)
        for(int j = 1; j <= m - 1; j++)
        {
            cin >> w;
            add(i * (m - 1) + j, (n - 1) * (m - 1) + i * (m - 1) + j, w);
        }
    spfa(s);
    cout << d[t] << endl;



    return 0;
}