单车模型的方向变化量

 

先解释一下侧偏角

汽车在行驶过程中，由于路面的侧向倾斜，侧向风或者曲线行驶时的离心力等的作用，车轮中心沿车轴方向产生一个侧向力F。因为车轮是有弹性的，所以，在侧向力F未达到车轮与地面间的最大摩擦力时，侧向力F使轮胎产生变形，使车轮倾斜，导致车轮行驶方向偏离预定的行驶路线。这种现象，就称为汽车轮胎的侧偏现象。

由于侧偏现象导致车轮实际运动的方向和车轮的方向不一致，其间的夹角就是侧偏角

 

运动学模型中的单车模型

这里先讨论在dt的时间内方向的变化量

 

使用自行车模型，我们基本上做了如下假设

• 和自行车一样，车辆是前轮驱动的
• 左右转向轮的角度和速度是一致的，也即左右轮享有同一个瞬时旋转中心 𝑂 。这样我们就能将左右轮压缩为一个轮子（这是使用自行车模型最大的好处，我们只用处理一个转向轮）
• 不需要考虑车辆的垂直运动
• 车辆是刚体

那么既然抽象成了单车，单车的特性也一目了然：

• 前轮的速度方向是沿着前轮的转向角方向（即前轮指向的方向）（这里不考虑侧偏角的影响）。
• 后轮的速度方向是沿着车辆纵向轴线的方向（即车辆的行驶方向）。
• 因为前轮和后轮都属于同一个刚体，它们的速度矢量都指向一个共同的旋转中心。

因此“瞬时转向中心（旋转中心）是车辆绕其旋转的点，它位于所有车轮的速度方向垂线线的交点处。”

ok，确认了旋转中心就可以画出单车模型的图了

 

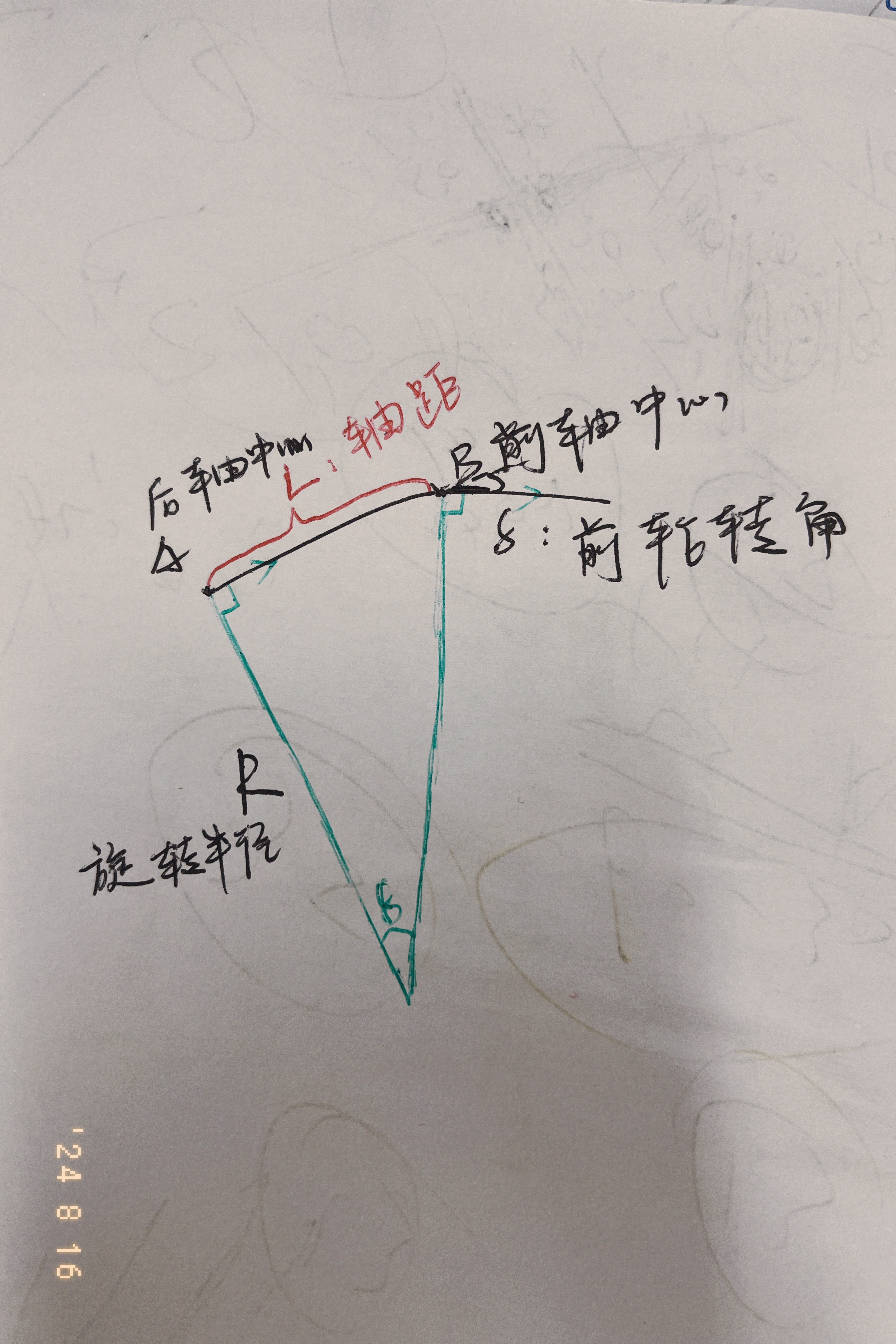
其中

A：后轴中心

B：前轴中心

L：轴距

R：旋转半径

\delta：前轮转角

 

如果我们想求主车在dt时间内的方向变化量怎么求呢？

设\omega为角速度

则

$$\triangle h=\omega *dt$$

根据线速度与角速度的关系

$$\omega =\frac{v}{R} $$

而根据图可知

$$R=\frac{L}{\tan \delta } $$

所以

 $$\triangle h=\frac{v*\tan\delta *dt }{L} $$