587. 安装栅栏 求凸包 Andrew's Algorithm

总结：

用于判断凸多边形内部点

给出任意多边形顶点，设A和B为其中两点且逆时针排序，C为内部一点，则向量AB叉乘向量AC小于0

如果是顺时针排序，则向量AB叉乘向量AC大于0

 

 

先按x从小到大，如果x相同，则y从小到大的顺序排序

已知x最小、y最小、x最大、y最大的点肯定为凸包上的点，为什么，可以仔细想想

因此，排序后的第一个肯定为凸包上的点

分两部分求

先求凸包的下半部分，再求上半部分

根据规则排序后，凸包下半部分的顶点，在数组中肯定是逆时针的顺序

先选数组中前两个点A、B放到凸包集合中，接下来遍历数组中剩下的每个点，

如第三个点C，判断，如果向量AB × 向量AC < 0   （叉积，＞0，说明C在B的里面），则说明点C在线段AB的外面，即C可能是一个凸包点，而B不是

满足右手螺旋定则，食指为第一个向量的方向

 

 

 

 

 

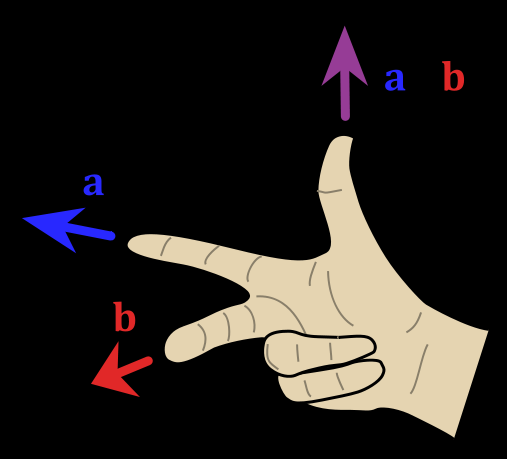
因此，从凸包集合中剔除B，加入C

如果 = 0，则说明共线，点C在直线AB上，直接加入凸包集合即可

否则，continue

想一下求余弦的公式就知道为啥了

 

 

当然如果选C时凸包中的点数大于2，比如有X、A、B，则如果B被剔除，则还要考虑A是否合适

举个栗子：

 

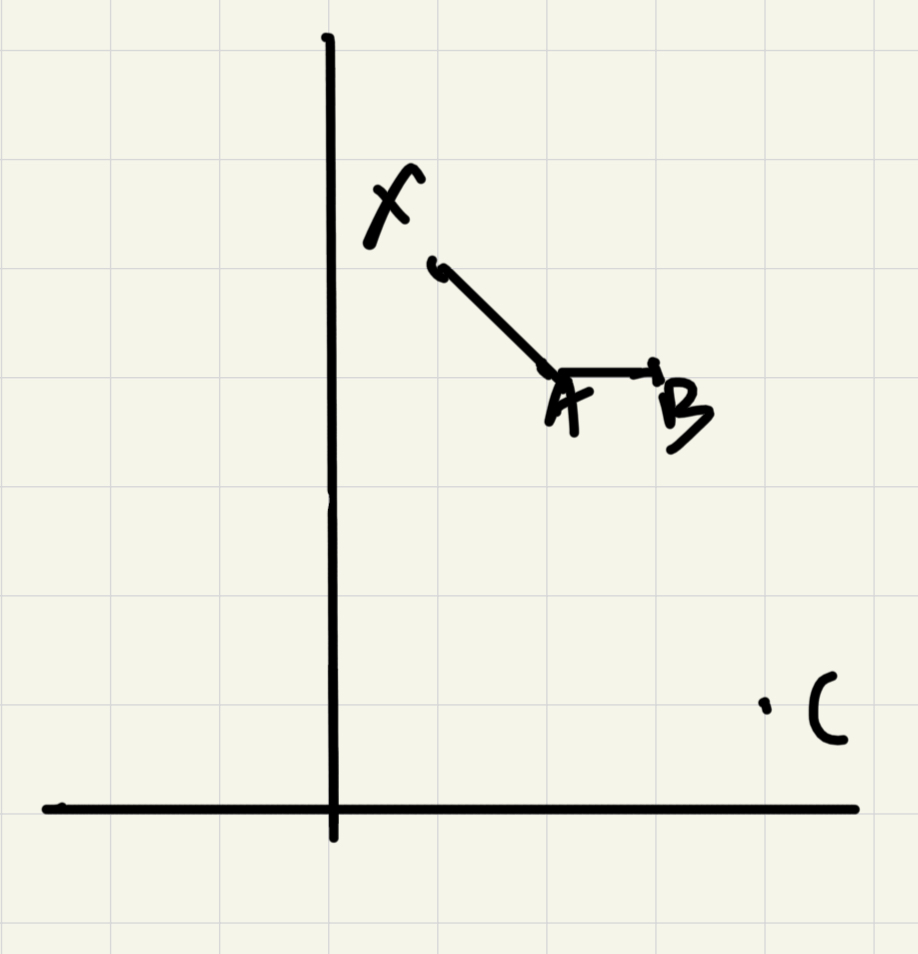
由上图可知，必须得判断A是否合适了吧

凸包上半部分的选点，数组从后向前遍历，这样就相当于x从大到小，如果x相同则y从大到小排序，保证了数组中上半部分凸包顶点的逆时针性质

代码如下

 

class Solution {
public:

    int xmul(vector<int> a, vector<int> b, vector<int> c)
    {
        return (b[0] - a[0]) * (c[1] - a[1]) - (b[1] - a[1]) * (c[0] - a[0]);
    }
    bool vis[110][110];
    vector<vector<int>> outerTrees(vector<vector<int>>& trees) {

        vector<vector<int>> v;
        memset(vis, 0, sizeof(vis));
        sort(trees.begin(), trees.end());
        int n = trees.size();
        for(int i = 0; i < n; i++)
        {
            while(v.size() >= 2 && xmul(v[v.size() - 2], v[v.size() - 1], trees[i]) < 0)
                vis[v[v.size() - 1][0]][v[v.size() -1][1]] =  0, v.pop_back();
            v.push_back(trees[i]);
            vis[trees[i][0]][trees[i][1]] = 1;
        }
        int k = v.size();
        for(int i = n - 2; i >= 0; i--)
        {
            while(v.size() >= k + 1 && xmul(v[v.size() - 2], v[v.size() - 1], trees[i]) < 0)
                v.pop_back();
            if(vis[trees[i][0]][trees[i][1]] == 0)
                v.push_back(trees[i]);
        }

        return v;
    }
};