神经网络层数增多 梯度消失、爆炸问题 以及 激活函数在反向传播中的作用

假设有一个三层全连接网络，设\(x_i\)为第i层网络的输入，\(f_i\)为第i层激活函数的输出，，则
\(x_i = f_{i - 1}\)

\(f_{i+1} = f(f_i * w + b)\)

注意现在x是已知的，要通过已知的x去训练w

设\(Loos = g(f_3)\)

则\(w_{3(new)} = w_{3(old)} - lr * \delta Loss / \delta w_{3(old)}\)

其中\(\delta Loss / \delta w_{3(old)} = \delta Loss / \delta f_3 * \delta f_3 / \delta w_{3(old)} = \delta Loss / \delta f_3 * f'_3(w_{3(old)})\)

推广得
\(\delta Loss / \delta w_{1(old)} = (\delta Loss / \delta f_3) * (\delta f_3 / \delta f_2) * (\delta f_2 / \delta f_1) * (\delta f_1 / w_{1(old)})\)

又因为\(x_i = f_{i - 1}\)，所以

\(\delta Loss / \delta w_{1(old)} = (\delta Loss / \delta f_3) * f'_3 * f'_2 * f'_1\)

tanh：

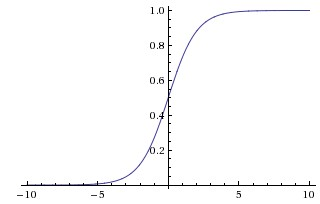
sigmoid：

relu：

图像可见，tanh和sigmoid当值较大时会发生饱和现象，导数较小，当网络很深时，传播到第一层时，梯度就会趋近于0，因此训练时拟合得较慢，训练时间就比较长
relu得导数要么是0要么是1，因此训练得就比较快。
梯度爆炸和消失：
对于\(f'_i\)
此部分大于1，那么层数增多的时候，最终的求出的梯度更新将以指数形式增加，即发生梯度爆炸，
如果此部分小于1，那么随着层数增多，求出的梯度更新信息将会以指数形式衰减，即发生了梯度消失。