WGAN的改进点和实操

包含三部分：1、WGAN改进点 2、代码修改 3、训练心得

一、WGAN的改进部分：

判别器最后一层去掉sigmoid （相当于最后一层做了一个y = x的激活）
生成器和判别器的loss不取log
每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c
不要用基于动量的优化算法（包括momentum和Adam），推荐RMSProp，SGD也行（这部分很玄学）

去掉sigmoid会出现什么问题？

优点：去掉sigmoid 只要二者存在差值就会学习让他们尽量小

缺点：去掉sigmoid 判别器的输出会到无穷大生成器也会到无穷大（只要二者的差值很小就满足条件）无法优化。

（公式1）

如何解决（上述）无法优化问题（loss可能一直上升）？

这就是WGAN的第三个改进点。（每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c）

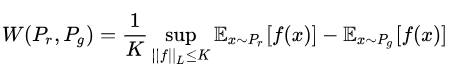（公式2）（作者用这个公式来表达，证明过程再论文附录中）

详细解读（这部分参看：https://blog.csdn.net/omnispace/article/details/54942668）

分析

首先需要介绍一个概念——Lipschitz连续。它其实就是在一个连续函数 $f$ 上面额外施加了一个限制，要求存在一个常数 $K\geq 0$ 使得定义域内的任意两个元素 $x_1$ 和 $x_2$ 都满足

$|f(x_1) - f(x_2)| \leq K |x_1 - x_2|$

此时称函数 $f$ 的Lipschitz常数为 $K$ 。

简单理解，比如说 $f$ 的定义域是实数集合，那上面的要求就等价于 $f$ 的导函数绝对值不超过 $K$ （这里是导数概念（f(x1) - f(x2)）/(x1-x2) 为导数）。再比如说 $\log (x)$ 就不是Lipschitz连续，因为它的导函数没有上界。Lipschitz连续条件限制了一个连续函数的最大局部变动幅度。

公式2的意思就是在要求函数 $f$ 的Lipschitz常数 $||f||_L$ 不超过 $K$ 的条件下，对所有可能满足条件的 $f$ 取到 $\mathbb{E}_{x \sim P_r} [f(x)] - \mathbb{E}_{x \sim P_g} [f(x)]$ 的上界，然后再除以 $K$ 。特别地，我们可以用一组参数 $w$ 来定义一系列可能的函数 $f_w$ ，此时求解公式2可以近似变成求解如下形式

$K \cdot W(P_r, P_g) \approx \max_{w: |f_w|_L \leq K} \mathbb{E}_{x \sim P_r} [f_w(x)] - \mathbb{E}_{x \sim P_g} [f_w(x)]$ （公式3）

再用上我们搞深度学习的人最熟悉的那一套，不就可以把 $f$ 用一个带参数 $w$ 的神经网络来表示嘛！由于神经网络的拟合能力足够强大，我们有理由相信，这样定义出来的一系列 $f_w$ 虽然无法囊括所有可能，但是也足以高度近似公式2要求的那个 $sup_{||f||_L \leq K}$ 了。

最后，还不能忘了满足公式3中 $||f_w||_L \leq K$ 这个限制。我们其实不关心具体的K是多少，只要它不是正无穷就行，因为它只是会使得梯度变大 $K$ 倍，并不会影响梯度的方向。所以作者采取了一个非常简单的做法，就是限制神经网络 $f_\theta$ 的所有参数 $w_i$ 的不超过某个范围 $[-c, c]$ ，比如 $w_i \in [- 0.01, 0.01]$ ，此时关于输入样本 $x$ 的导数 $\frac{\partial f_w}{\partial x}$ 也不会超过某个范围，所以一定存在某个不知道的常数 $K$ 使得 $f_w$ 的局部变动幅度不会超过它，Lipschitz连续条件得以满足。具体在算法实现中，只需要每次更新完 $w$ 后把它clip回这个范围就可以了。

到此为止，我们可以构造一个含参数 $w$ 、最后一层不是非线性激活层的判别器网络 $f_w$ ，在限制 $w$ 不超过某个范围的条件下，使得

$L = \mathbb{E}_{x \sim P_r} [f_w(x)] - \mathbb{E}_{x \sim P_g} [f_w(x)]$ （公式4）

尽可能取到最大，此时 $L$ 就会近似真实分布与生成分布之间的Wasserstein距离（忽略常数倍数 $K$ ）。注意原始GAN的判别器做的是真假二分类任务，所以最后一层是sigmoid，但是现在WGAN中的判别器 $f_w$ 做的是近似拟合Wasserstein距离，属于回归任务，所以要把最后一层的sigmoid拿掉。

接下来生成器要近似地最小化Wasserstein距离，可以最小化 $L$ ，由于Wasserstein距离的优良性质，我们不需要担心生成器梯度消失的问题。再考虑到 $L$ 的第一项与生成器无关，就得到了WGAN的两个loss。

二、代码修改：

根据改进的四个部分来修改代码（TF下）：

加变量：

1 CLIP = [-0.01, 0.01]  #用来截断w（第三个改进点）
2 CRITIC_NUM = 5     #权衡训练次数  Discrimnator要训练的比Genenrator多（5 次Discrimnator 一次 G）

① 判别器最后一层去掉sigmoid

1 return tf.nn.sigmoid(h4), h4
2 替换后：
3 return h4, h4

② 生成器和判别器的loss不取log

原始的GAN loss为：

min _Gmax_D E_x_∼_q₍_x₎[logD(x)]+E_z_∼_p₍_z₎[log(1−D(G(z)))

去掉log为 min _Gmax_D D(x) + 1−D(G(z)）

由于最大化D 我们在代码中应该加 “-” D loss: min_D -（D(x) + 1−D(G(z)））

G loss min_G−D(G(z)）

1 self.d_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=self.D_logits, labels=tf.ones_like(self.D)))
2 self.d_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=self.D_logits_, labels=tf.zeros_like(self.D_)))
3 self.g_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=self.D_logits_, labels=tf.ones_like(self.D_))) \
4 self.d_loss = self.d_loss_real + self.d_loss_fake

修改D loss为：

1 self.d_loss_real = tf.reduce_mean(self.D_logits)
2 self.d_loss_fake = -tf.reduce_mean(self.D_logits_)
3 self.d_loss = -(self.d_loss_real + self.d_loss_fake)

修改G loss为：

1 self.g_loss = -tf.reduce_mean(self.D_logits_)

③ ④ 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c(放到参数更新后) 修改优化器

原始：

1 d_optim = tf.train.AdamOptimizer(args.lr, beta1=args.beta1) \
2                           .minimize(self.d_loss, var_list=self.d_vars)
3 g_optim = tf.train.AdamOptimizer(args.lr, beta1=args.beta1) \
4                           .minimize(self.g_loss, var_list=self.g_vars)

修改为：

1 d_optim = tf.train.RMSPropOptimizer(args.lr, beta1=args.beta1) \
2             .minimize(self.d_loss, var_list=self.d_vars)
3 g_optim = tf.train.RMSPropOptimizer(args.lr, beta1=args.beta1) \
4             .minimize(self.g_loss, var_list=self.g_vars)
5 clip_d_op = [var.assign(tf.clip_by_value(var, CILP[0], CILP[1])) for var in self.d_vars]     #进行截断

三、训练心得：

一、权重

a. 调节Generator loss中GAN loss的权重
G loss和Gan loss在一个尺度上或者G loss比Gan loss大一个尺度。但是千万不能让Gan loss占主导地位, 这样整个网络权重会被带偏。

二、训练次数
b. 调节Generator和Discrimnator的训练次数比
一般来说，Discrimnator要训练的比Genenrator多。比如训练五次Discrimnator，再训练一次Genenrator(WGAN论文是这么干的)。

三、学习率
c. 调节learning rate
这个学习速率不能过大。一般要比Genenrator的速率小一点。

四、优化器
d. Optimizer的选择不能用基于动量法的
如Adam和momentum。可使用RMSProp或者SGD。

五、结构
e. Discrimnator的结构可以改变
如果用WGAN，判别器的最后一层需要去掉sigmoid。但是用原始的GAN，需要用sigmoid，因为其loss function里面需要取log，所以值必须在[0,1]。这里用的是邓炜的critic模型当作判别器。之前twitter的论文里面的判别器即使去掉了sigmoid也不好训练。

posted @ 2019-07-26 10:07 WSX_1994 阅读(4788) 评论(0) 编辑收藏举报

刷新页面返回顶部

WSX_WOLF