一维数组子数组求最大和

#include <iostream> 
#include <algorithm> 
using namespace std; 
#define MAXN 1003 
int A[MAXN]; 
int Tail[MAXN]; 
 // 动态规划思想，时间复杂度O(n) 
int main() 
{ 
    int length;    //数组长度
    int   i;       //循环变量
    int  tail;     //记录数组结束的位置 
    cout<<"please input the length of array:"<<endl;
    cin >> length; 
    cout<<"please input every number of array:"<<endl;
    for (i=1; i<=length; i++) 
    {
        cin >> A[i]; 
    }                                               // 计算以tail结尾的子数组之和的最大值，即子数组包含第k个数 
    Tail[1] = A[1]; 
    for (tail=2; tail<=length; tail++)                   // tail个阶段 
    {                                 
        Tail[tail] = max(A[tail],Tail[tail-1]+A[tail]); 
    }                                              // 只有两个状态 
                                                   // 因为和最大的子数组肯定以某个数结尾，所以取这length个子数组的最大值
    int All = Tail[1]; 
    for (i=2; i<=length; i++) 
        All = max(All, Tail[i]); 
    cout << "MAX :  "<<All<<"  !"<<endl; 
} 

返回一个整数数组中最大子数组的和，细化分析：
1，在所有以元素tail结尾的子数组中，选出元素和最大的子数组，tail=1,2...n。
2，以元素k结尾的和最大的子数组是包含以元素tail-1结尾的和最大的子数组还是就只有元素tail这一个元素，一共有这两个可选状态。

3，在得到以每个元素结尾的和最大的子数组之后，只要取其中最大值就是所有子数组中最大的子数组。

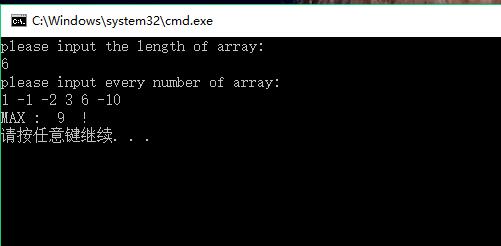
总结：

这个题目乍一看好像很简单但是还是花了一点时间，主要是把重点放在时间复杂度上了，还是经验不足，思路很狭隘。

结对编程伙伴：李妍 20133099 博客地址：http://www.cnblogs.com/liyan-luckygirl/