数列分块入门
数列分块入门
算是入门了吧
写在前面
本人十分之 Naive 所以写的不好还请见谅。
前置知识
- 暴力
线段树
线段树貌似也不太需要,但本文建立在你已经会线段树的基础上。但真有人先学分块再学线段树的嘛?
前置思想
先插一个题外话,以下题目均在Loj上。Luogu在这方面略有欠缺。
好的,回到正题。严格来讲,分块是一种处理数据的思想,而非数据结构。
我们先从最经典的问题来一步一步了解分块:
LOJ #6277. 数列分块入门 1
来看这一道题。非常显然,这题可以用线段树秒杀,但我们要学习分块。
在线段树上,我们把区间分为了 \(\log{n}\) 个子区间,单独维护它们的信息,并且根据它们信息的可加性,维护处一整段的信息。
而分块是这样子的:
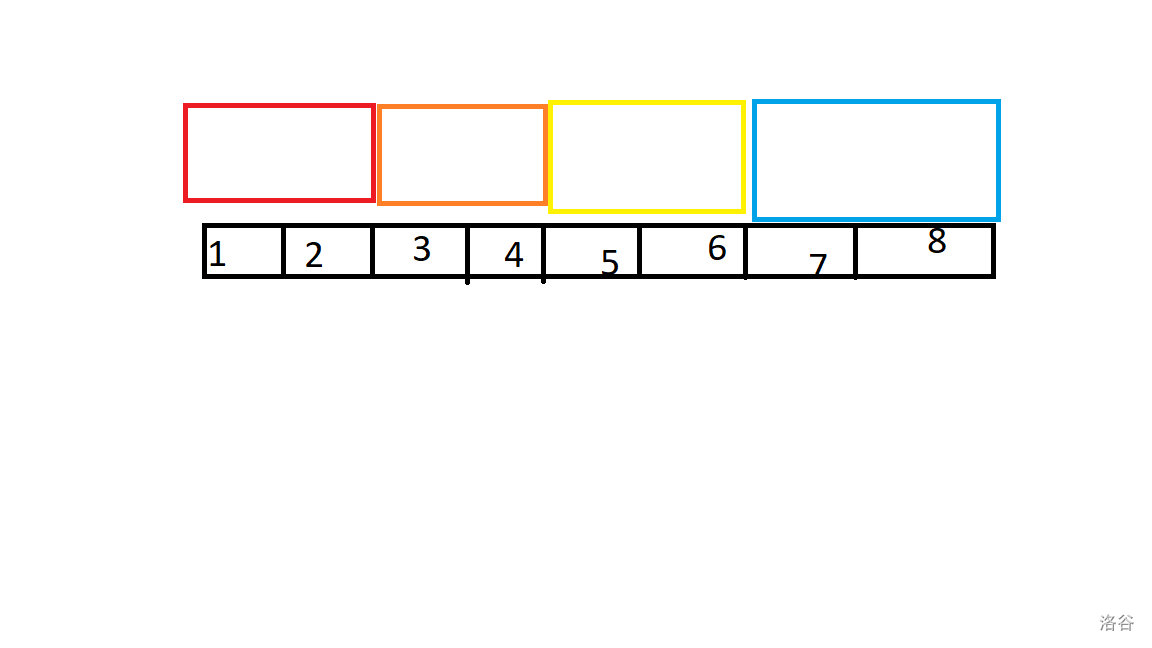
如题,我们完美的把这八个元素分成了四个块。我们可以维护每个块的信息。对于每一次查询一个区间问题,我们只需要暴力地把每个查询区间完整块内的答案加起来,再计算零散的元素的贡献,即可获得答案。
以此题为例,查询2到7的时候流程是这样的:

这东西看着就很不靠谱是吧。。。。但是如果我们把块长设为 \(\sqrt{n}\) ,它的时间复杂度就蜕变为了 \(O(n \sqrt{n})\)
分块的时间复杂度主要取决于分块的块长,一般可以通过均值不等式求出某个问题下的最优块长,以及相应的时间复杂度。
那这东西对比线段树有什么优势呢???
我个人认为,这东西与线段树,就好像树状数组与线段树。分块处理的信息并不需要满足线段可加性,但线段树是 \(\log\),分块是 \(\sqrt\)。
到此为止,分块入门基本上就讲完了。
对于本题,细节看代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 50005;
#define int long long
int a[maxn], sum[maxn], add[maxn];
int id[maxn];
int L[maxn], R[maxn];
int n, t;
void addd(int l, int r, int y){
int p = id[l], q = id[r];
if(p == q){ // 如果属于一个块就暴力加
for(int i = l; i <= r; i++){
a[i] += y;
}
sum[p] += y*(r-l+1);//记得更新当前块的和
}else{
for(int i = p+1; i <= q-1; i++) add[i] += y; // 大块直接加tag
for(int i = l; i <= R[p]; i++) a[i] += y; // 小块暴力加
for(int i = r; i >= L[q]; i--) a[i] += y; // 小块暴力加
sum[p] += y * (R[p] - l + 1);//记得更新当前块的和
sum[q] += y * (r - L[q] + 1);//记得更新当前块的和
}
}
signed main(){
cin>>n;
for(int i = 1; i <= n; i++) cin>>a[i];
int t = sqrt(n); // t为块长
for(int i = 1; i <= n; i++) id[i] = (i-1)/t+1; // id记录了a[i]属于哪个块
for(int i = 1; i <= n; i++) sum[id[i]] += a[i];//块信息预处理
for(int i = 1; i <= id[n]; i++) L[i]=(i-1)*t+1,R[i]=i*t;//L[i]为第i个块的左端点,R[i]为右端点
R[id[n]] = n;//需要特判一下最后一个块不完整的情况
for(int i = 1; i <= n; i++){
int op, l, r, c;
cin>>op>>l>>r>>c;
if(op) cout<<a[r] + add[id[r]]<<endl; // 输出a[i] + tag
else addd(l, r, c);
}
return 0;
}
LOJ #6280. 数列分块入门 4
同上,直接看代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 50005;
#define int long long
int a[maxn], sum[maxn], add[maxn];
int id[maxn];
int L[maxn], R[maxn];
int n, t;
void addd(int l, int r, int y){
int p = id[l], q = id[r];
if(p == q){ // 如果属于一个块就暴力加
for(int i = l; i <= r; i++){
a[i] += y;
}
sum[p] += y*(r-l+1);//记得更新当前块的和
}else{
for(int i = p+1; i <= q-1; i++) add[i] += y; // 大块直接加tag
for(int i = l; i <= R[p]; i++) a[i] += y; // 小块暴力加
for(int i = r; i >= L[q]; i--) a[i] += y; // 小块暴力加
sum[p] += y * (R[p] - l + 1);//记得更新当前块的和
sum[q] += y * (r - L[q] + 1);//记得更新当前块的和
}
}
int q(int l, int r, int c){
int p = id[l], q = id[r];
int ans = 0;
if(p == q){//同块直接暴力统计答案
for(int i = l; i <= r; i++){
ans += a[i];
ans %= c;
}
ans += add[p] % c * (r-l+1) % c;
ans %= c;
return ans;
}
for(int i = p+1; i <= q-1; i++){
ans += sum[i] % c + add[i] % c * (R[i] - L[i] + 1) % c; //统计中间完整块的答案
}
for(int i = l; i <= R[p]; i++) ans += a[i], ans %= c;//散块
for(int i = r; i >= L[q]; i--) ans += a[i], ans %= c;//散块
ans += add[p] % c * (R[p] - l + 1) % c;
ans %= c;
ans += add[q] % c * (r - L[q] + 1) % c;
ans %= c;
return ans;
}
signed main(){
cin>>n;
for(int i = 1; i <= n; i++) cin>>a[i];
int t = sqrt(n); // t为块长
for(int i = 1; i <= n; i++) id[i] = (i-1)/t+1; // id记录了a[i]属于哪个块
for(int i = 1; i <= n; i++) sum[id[i]] += a[i];//块信息预处理
for(int i = 1; i <= id[n]; i++) L[i]=(i-1)*t+1,R[i]=i*t;//L[i]为第i个块的左端点,R[i]为右端点
R[id[n]] = n;//需要特判一下最后一个块不完整的情况
for(int i = 1; i <= n; i++){
int op, l, r, c;
cin>>op>>l>>r>>c;
if(op) cout<<q(l, r, c+1)<<endl;
else addd(l, r, c);
}
return 0;
}
LOJ#6278. 数列分块入门 2
有趣的题,请你确保理解了上面的题。
好的,这道题求小于 \(x\) 的数的个数。如果是在有序的序列,那我们肯定会做,直接二份即可。
考虑使用分块,对于每一个块,进行块内排序,即:
for(int i = 1; i <= t; i++){
sort(a+L[i], a+R[i]+1);
}
这样子,我们就可以二分每一个块进行暴力统计,对于每一个散的元素,直接在原数组上暴力统计即可。太暴力了!
总时间复杂度 \(O(n\log{n} + n\sqrt{n}\log{n})\)
注:我的代码中b为原数组
#include<bits/stdc++.h>
using namespace std;
const int MAX = 50005;
int a[MAX];
int b[MAX];
int id[MAX];
int pls[MAX];
int L[MAX], R[MAX];
void add(int l, int r, int c){
int p = id[l], q = id[r];
if(p == q){
for(int i = l; i <= r; i++) b[i] += c;
for(int i = L[p]; i <= R[p]; i++){
a[i] = b[i];
}
sort(a+L[p], a+R[p]+1);
}else{
for(int i = p+1; i <= q-1; i++) pls[i] += c;
for(int i = l; i <= R[p]; i++) b[i] += c;
for(int i = L[p]; i <= R[p]; i++) a[i] = b[i];
sort(a+L[p], a+R[p]+1);
for(int i = r; i >= L[q]; i--) b[i] += c;
for(int i = L[q]; i <= R[q]; i++) a[i] = b[i];
sort(a+L[q], a+R[q]+1);
}
}
int query(int l, int r, int c){
int p = id[l], q = id[r];
if(p == q){
int ans = 0;
for(int i = l; i <= r; i++) if(b[i] + pls[p] < c) ans++;
return ans;
}else{
int ans = 0;
for(int i = p+1; i <= q-1; i++){
int x1 = lower_bound(a+L[i], a+R[i]+1, c-pls[i]) - a - L[i];
ans += x1;
}
for(int i = l; i <= R[p]; i++) if(b[i] + pls[p] < c) ans++;
for(int i = L[q]; i <= r; i++) if(b[i] + pls[q] < c) ans++;
return ans;
}
}
signed main(){
int n;
cin>>n;
for(int i = 1; i <= n; i++) cin>>a[i], b[i] = a[i];
int t = sqrt(n); // t为块长
for(int i = 1; i <= n; i++) id[i] = (i-1)/t+1; // id记录了a[i]属于哪个块
for(int i = 1; i <= id[n]; i++) L[i]=(i-1)*t+1,R[i]=i*t;//L[i]为第i个块的左端点,R[i]为右端点
R[id[n]] = n;//需要特判一下最后一个块不完整的情况
for(int i = 1; i <= t; i++){
sort(a+L[i], a+R[i]+1);
}
for(int i = 1; i <= n; i++){
int op, l, r, c;
cin>>op>>l>>r>>c;
if(op == 0){
add(l, r, c);
}else{
cout<<query(l, r, c*c)<<endl;
}
}
return 0;
}
LOJ #6279. 数列分块入门 3
同上
#include<bits/stdc++.h>
using namespace std;
static char buf[1000000],*p1=buf,*p2=buf;
#define getchar() p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++
inline int read(){int x=0,f=1;char c=getchar();while(c<'0' || c>'9'){if(c=='-') f=-1;c=getchar();}while(c>='0' && c<='9') {x=x*10+c-48;c=getchar();}return x*f;}
inline void write(int x){static char buf[20];static int len=-1;if(x<0)putchar('-'),x=-x;do buf[++len]=x%10,x/=10;while(x);while(len>=0)putchar(buf[len--]+'0');}
const int MAX = 1e5+10;
int a[MAX];
int b[MAX];
int id[MAX];
int pls[MAX];
int L[MAX], R[MAX];
void add(int l, int r, int c){
int p = id[l], q = id[r];
if(p == q){
for(int i = l; i <= r; i++) b[i] += c;
for(int i = L[p]; i <= R[p]; i++){
a[i] = b[i];
}
sort(a+L[p], a+R[p]+1);
}else{
for(int i = p+1; i <= q-1; i++) pls[i] += c;
for(int i = l; i <= R[p]; i++) b[i] += c;
for(int i = L[p]; i <= R[p]; i++) a[i] = b[i];
sort(a+L[p], a+R[p]+1);
for(int i = r; i >= L[q]; i--) b[i] += c;
for(int i = L[q]; i <= R[q]; i++) a[i] = b[i];
sort(a+L[q], a+R[q]+1);
}
}
int query(int l, int r, int c){
int p = id[l], q = id[r];
if(p == q){
int ans = -0x3f3f3f3f;
for(int i = l; i <= r; i++) if(b[i] + pls[p] < c) ans = max(ans, b[i]+pls[p]);
return ans;
}else{
int ans = -0x3f3f3f3f;
for(int i = p+1; i <= q-1; i++){
int x1 = lower_bound(a+L[i], a+R[i]+1, c-pls[i]) - a;
if(x1 == L[i]) continue;
ans = max(ans, a[x1-1]+pls[i]);
}
for(int i = l; i <= R[p]; i++) if(b[i] + pls[p] < c) ans = max(ans, b[i]+pls[p]);
for(int i = L[q]; i <= r; i++) if(b[i] + pls[q] < c) ans = max(ans, b[i]+pls[q]);
return ans;
}
}
signed main(){
int n = read();
for(int i = 1; i <= n; i++) a[i] = read(), b[i] = a[i];
int t = sqrt(n); // t为块长
for(int i = 1; i <= n; i++) id[i] = (i-1)/t+1; // id记录了a[i]属于哪个块
for(int i = 1; i <= id[n]; i++) L[i]=(i-1)*t+1,R[i]=i*t;//L[i]为第i个块的左端点,R[i]为右端点
R[id[n]] = n;//需要特判一下最后一个块不完整的情况
for(int i = 1; i <= t; i++){
sort(a+L[i], a+R[i]+1);
}
for(int i = 1; i <= n; i++){
int op = read(), l = read(), r = read(), c = read();
if(op == 0){
add(l, r, c);
}else{
int ans = query(l, r, c);
if(ans == -0x3f3f3f3f) puts("-1");
else write(ans), putchar('\n');
}
}
return 0;
}
LOJ #6281. 数列分块入门 5
双倍经验:https://www.luogu.com.cn/problem/SP2713
https://www.luogu.com.cn/problem/P4145
很巧妙的一道题。
考虑到1e12的数开6次方就变成了1,再对它进行操作就没有意义了。所以我们对于数据分块,对于每个块,如果每个数都变成了1,那就不用去操作它了。
复杂度我不太会算,大概是: \(O(n\sqrt{n})\) 的吧。不过这题稍加思考就可以用线段树代替分块实现 \(\log\) 解法。
代码:
#include<bits/stdc++.h>
using namespace std;
static char buf[1000000],*p1=buf,*p2=buf;
#define getchar() p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++
inline int read(){int x=0,f=1;char c=getchar();while(c<'0' || c>'9'){if(c=='-') f=-1;c=getchar();}while(c>='0' && c<='9') {x=x*10+c-48;c=getchar();}return x*f;}
inline void write(int x){static char buf[20];static int len=-1;if(x<0)putchar('-'),x=-x;do buf[++len]=x%10,x/=10;while(x);while(len>=0)putchar(buf[len--]+'0');}
const int maxn = 200010;
#define int long long
int a[maxn], sum[maxn], pls[maxn];
int id[maxn];
int L[maxn], R[maxn];
int n, t;
void add(int l, int r){
int p = id[l], q = id[r];
if(p == q){
if(sum[p] == R[p]-L[p]+1) return ;
for(int i = l; i <= r; i++){
sum[p] -= a[i];
a[i] = sqrt(a[i]);
sum[p] += a[i];
}
}else{
if(sum[p] != R[p] - L[p] + 1) for(int i = l; i <= R[p]; i++) sum[p] -= a[i], a[i] = sqrt(a[i]), sum[p] += a[i];
if(sum[q] != R[q] - L[q] + 1) for(int i = r; i >= L[q]; i--) sum[q] -= a[i], a[i] = sqrt(a[i]), sum[q] += a[i];
for(int i = p+1; i <= q-1; i++) if(sum[i] != R[i] - L[i] + 1) for(int j = L[i]; j <= R[i]; j++) sum[i] -= a[j], a[j] = sqrt(a[j]), sum[i] += a[j];
}
}
int query(int l, int r){
int p = id[l], q = id[r];
int ans = 0;
if(p == q){
for(int i = l; i <= r; i++) ans += a[i];
return ans;
}else{
for(int i = p+1; i <= q-1; i++) ans += sum[i];
for(int i = l; i <= R[p]; i++) ans += a[i];
for(int i = L[q]; i <= r; i++) ans += a[i];
return ans;
}
}
signed main(){
n = read();
for(int i = 1; i <= n; i++) a[i] = read();
int t = sqrt(n); // t为块长
for(int i = 1; i <= n; i++) id[i] = (i-1)/t+1; // id记录了a[i]属于哪个块
for(int i = 1; i <= n; i++) sum[id[i]] += a[i];//块信息预处理
for(int i = 1; i <= id[n]; i++) L[i]=(i-1)*t+1,R[i]=i*t;//L[i]为第i个块的左端点,R[i]为右端点
R[id[n]] = n;//需要特判一下最后一个块不完整的情况
for(int i = 1; i <= n; i++){
int op = read(), l = read(), r = read(), c = read();
if(l > r) swap(l, r);
if(op) cout<<query(l, r)<<endl;
else add(l, r);
}
return 0;
}
LOJ #6282. 数列分块入门 6
挺无聊的题。直接对于数据分块,然后暴力插入。
#include<bits/stdc++.h>
using namespace std;
#define int long long
static char buf[1000000],*p1=buf,*p2=buf;
#define getchar() p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++
inline int read(){int x=0,f=1;char c=getchar();while(c<'0' || c>'9'){if(c=='-') f=-1;c=getchar();}while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+c-48;c=getchar();}return x*f;}
inline void write(int x){static char buf[20];static int len=-1;if(x<0)putchar('-'),x=-x;do buf[++len]=x%10,x/=10;while(x);while(len>=0)putchar(buf[len--]+48);}
const int MAX = 300005;
int a[MAX], id[MAX];
vector <int> v[MAX];
int n;
void add(int x, int val){
for(int i = 1; i <= id[n]; i++){
if(x <= v[i].size()){
auto pos = v[i].begin();
for(int i = 1; i < x; i++) pos++;
v[i].insert(pos, val);
return ;
}else{
x -= v[i].size();
}
}
}
int query(int x){
for(int i = 1; i <= id[n]; i++){
if(x <= v[i].size()) return v[i][x-1];
else x -= v[i].size();
}
}
signed main(){
n = read();
int t = sqrt(n);
for(int i = 1; i <= n; i++) a[i] = read(), id[i] = (i-1)/t+1, v[id[i]].push_back(a[i]);
for(int i = 1; i <= n; i++){
int op = read(), l = read(), r = read(), c = read();
if(op == 0) add(l, r);
else write(query(r)), puts("");
}
return 0;
}
LOJ#6283. 数列分块入门 7
同https://www.luogu.com.cn/problem/P3373
懒得写了。。。。。
LOJ#6284. 数列分块入门 8
区间推平???珂朵莉树???
然而这题只需要对于每一个区间打一个修改tag即可。需要再改。
#include<bits/stdc++.h>
using namespace std;
static char buf[1000000],*p1=buf,*p2=buf;
#define getchar() p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++
inline int read(){int x=0,f=1;char c=getchar();while(c<'0' || c>'9'){if(c=='-') f=-1;c=getchar();}while(c>='0' && c<='9') {x=x*10+c-48;c=getchar();}return x*f;}
inline void write(int x){static char buf[20];static int len=-1;if(x<0)putchar('-'),x=-x;do buf[++len]=x%10,x/=10;while(x);while(len>=0)putchar(buf[len--]+'0');}
const int maxn = 100005;
#define int long long
int a[maxn], sum[maxn], pls[maxn];
int id[maxn];
int L[maxn], R[maxn];
int n, t;
void add(int l, int r, int c){
int p = id[l], q = id[r];
if(p == q){
if(sum[p] != c){
if(sum[p] != 0)for(int i = L[q]; i <= R[q]; i++) a[i] = sum[p];
sum[p] = 0;
for(int i = l; i <= r; i++) a[i] = c;
}
}else{
if(sum[p] != c){
if(sum[p] != 0)for(int i = L[p]; i < l; i++) a[i] = sum[p];
sum[p] = 0;
for(int i = l; i <= R[p]; i++) a[i] = c;
}
if(sum[q] != c){
if(sum[q] != 0)for(int i = L[q]; i <= R[q]; i++) a[i] = sum[q];
sum[q] = 0;
for(int i = r; i >= L[q]; i--) a[i] = c;
}
for(int i = p+1; i <= q-1; i++) sum[i] = c;
}
}
int query(int l, int r, int c){
int p = id[l], q = id[r];
int ans = 0;
if(p == q){
if(sum[p] == c) ans += r-l+1;
else if(sum[p] == 0)for(int i = l; i <= r; i++) ans += a[i] == c;
return ans;
}else{
for(int i = p+1; i <= q-1; i++){
if(sum[i] == c) ans += R[i] - L[i] + 1;
else if(sum[i] == 0) for(int j = L[i]; j <= R[i]; j++) ans += a[j] == c;
}
if(sum[p] == c){
ans += R[p] - l + 1;
}else if(sum[p] == 0){
for(int i = l; i <= R[p]; i++) ans += a[i] == c;
}
if(sum[q] == c){
ans += r - L[q] + 1;
}else if(sum[q] == 0){
for(int i = L[q]; i <= r; i++) ans += a[i] == c;
}
return ans;
}
}
signed main(){
n = read();
for(int i = 1; i <= n; i++) a[i] = read();
int t = sqrt(n); // t为块长
for(int i = 1; i <= n; i++) id[i] = (i-1)/t+1; // id记录了a[i]属于哪个块
for(int i = 1; i <= id[n]; i++) L[i]=(i-1)*t+1,R[i]=i*t;//L[i]为第i个块的左端点,R[i]为右端点
R[id[n]] = n;//需要特判一下最后一个块不完整的情况
for(int i = 1; i <= n; i++){
int l = read(), r = read(), c = read();
write(query(l, r, c));
putchar('\n');
add(l, r, c);
}
return 0;
}
LOJ#6285. 数列分块入门 9
luogu:https://www.luogu.com.cn/problem/P4168
挺有意思的题目。
记 \(s[i][j]\) 为前 \(i\) 个块元素 \(j\) 出现的个数。
\(f[i][j]\) 为 \(i\) 到 \(j\) 块的区间最小众数。
我们惊讶地发现 \(s\) 和 \(f\) 均可以通过 \(n\sqrt{n}\) 的时间内预处理,然后就做完了。
#include<bits/stdc++.h>
using namespace std;
static char buf[1000000],*p1=buf,*p2=buf;
#define getchar() p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++
inline int read(){int x=0,f=1;char c=getchar();while(c<'0' || c>'9'){if(c=='-') f=-1;c=getchar();}while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+c-48;c=getchar();}return x*f;}
inline void write(int x){static char buf[20];static int len=-1;if(x<0)putchar('-'),x=-x;do buf[++len]=x%10,x/=10;while(x);while(len>=0)putchar(buf[len--]+48);}
const int MAX = 50005;
const int MAX2 = 300;
int n, m;
int n2, num, t2;
int a[MAX], b[MAX];
int id[MAX], L[MAX], R[MAX];
int s[MAX2][MAX], f[MAX2][MAX2];
int t[MAX];
int query(int l, int r){
int p = id[l], q = id[r];
int ans = 0;
if(p == q){
for(int i = l; i <= r; i++) t[a[i]]++;
for(int i = l; i <= r; i++) if(t[a[i]] > t[ans] or (t[a[i]] == t[ans] and a[i] < ans)) ans = a[i];
for(int i = l; i <= r; i++) t[a[i]] = 0;
}else{
ans = f[p+1][q-1];
for(int i = l; i <= R[p]; i++) t[a[i]]++;
for(int i = L[q]; i <= r; i++) t[a[i]]++;
for(int i = l; i <= R[p]; i++){
int temp = s[q-1][a[i]] - s[p][a[i]] + t[a[i]], anss = s[q-1][ans] - s[p][ans] + t[ans];
if(temp > anss or (temp == anss and ans > a[i])) ans = a[i];
}
for(int i = L[q]; i <= r; i++){
int temp = s[q-1][a[i]] - s[p][a[i]] + t[a[i]], anss = s[q-1][ans] - s[p][ans] + t[ans];
if(temp > anss or (temp == anss and ans > a[i])) ans = a[i];
}
for(int i = l; i <= R[p]; i++) t[a[i]] = 0;
for(int i = L[q]; i <= r; i++) t[a[i]] = 0;
}
return ans;
}
int main(){
n = read(), m = read();
for(int i = 1; i <= n; i++) b[i] = a[i] = read();
t2 = sqrt(n);
for(int i = 1; i <= n; i++) id[i] = (i-1)/t2+1;
for(int i = 1; i <= id[n]; i++) L[i] = (i-1)*t2+1, R[i] = i*t2;
R[id[n]] = n;
sort(b+1, b+n+1);
n2 = unique(b+1, b+n+1) - b - 1;
for(int i = 1; i <= n; i++) a[i] = lower_bound(b+1, b+n2+1, a[i]) - b;
num = id[n];
for(int i = 1; i <= num; i++){
for(int j = L[i]; j <= R[i]; j++) s[i][a[j]]++;
for(int j = 1; j <= n2; j++) s[i][j] += s[i-1][j];
}
for(int i = 1; i <= num; i++){
for(int j = i; j <= num; j++){
int maxn = f[i][j-1];
for(int k = L[j]; k <= R[j]; k++){
if(s[j][a[k]] - s[i-1][a[k]] > s[j][maxn] - s[i-1][maxn] or (s[j][a[k]] - s[i-1][a[k]] == s[j][maxn] - s[i-1][maxn] and a[k] < maxn)){
maxn = a[k];
}
}
f[i][j] = maxn;
}
}
int last = 0;
for(int i = 1; i <= m; i++){
int l = ((read() + last - 1) % n) + 1, r = ((read() + last - 1) % n) + 1;
if(l > r) swap(l, r);
int ans = query(l, r);
write(b[ans]);
last = b[ans];
puts("");
}
return 0;
}
Ex练习
- luogu P4135 作诗 类似蒲公英
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
static char buf[1000000],*p1=buf,*p2=buf;
#define getchar() p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++
inline int read(){int x=0,f=1;char c=getchar();while(c<'0' || c>'9'){if(c=='-') f=-1;c=getchar();}while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+c-48;c=getchar();}return x*f;}
inline void write(int x){static char buf[20];static int len=-1;if(x<0)putchar('-'),x=-x;do buf[++len]=x%10,x/=10;while(x);while(len>=0)putchar(buf[len--]+48);}
const int MAX = 100005;
const int MAX2 = 400;
int n, m;
int n2, num, t2;
int a[MAX], b[MAX];
int id[MAX], L[MAX], R[MAX];
int s[MAX2][MAX], f[MAX2][MAX2];
int t[MAX];
bool vis[MAX];
int query(int l, int r){
int p = id[l], q = id[r];
int ans = 0;
if(p == q){
for(int i = l; i <= r; i++) t[a[i]]++;
for(int i = l; i <= r; i++){
if(vis[a[i]]) continue;
if(t[a[i]] % 2 == 0) ans++;
vis[a[i]] = 1;
}
for(int i = l; i <= r; i++) t[a[i]] = 0, vis[a[i]] = 0;
}else{
ans = f[p+1][q-1];
for(int i = l; i <= R[p]; i++) t[a[i]]++;
for(int i = L[q]; i <= r; i++) t[a[i]]++;
for(int i = l; i <= R[p]; i++){
if(vis[a[i]]) continue;
int temp = s[q-1][a[i]] - s[p][a[i]] + t[a[i]];
int pre = s[q-1][a[i]] - s[p][a[i]];
if(vis[a[i]]) continue;
if(temp % 2 == 1 and pre % 2 == 0 and temp > 0 and pre > 0) ans--;
if(temp % 2 == 0 and pre % 2 == 1 and temp > 0 and pre > 0) ans++;
if(temp % 2 == 0 and pre == 0 and temp > 0) ans++;
vis[a[i]] = 1;
}
for(int i = L[q]; i <= r; i++){
if(vis[a[i]]) continue;
int temp = s[q-1][a[i]] - s[p][a[i]] + t[a[i]];
int pre = s[q-1][a[i]] - s[p][a[i]];
if(temp % 2 == 1 and pre % 2 == 0 and temp > 0 and pre > 0) ans--;
if(temp % 2 == 0 and pre % 2 == 1 and temp > 0 and pre > 0) ans++;
if(temp % 2 == 0 and pre == 0 and temp > 0) ans++;
vis[a[i]] = 1;
}
for(int i = l; i <= R[p]; i++) t[a[i]] = 0, vis[a[i]] = 0;
for(int i = L[q]; i <= r; i++) t[a[i]] = 0, vis[a[i]] = 0;
}
return ans;
}
signed main(){
int rub;
n = read(), rub = read(), m = read();
for(int i = 1; i <= n; i++) b[i] = a[i] = read();
t2 = sqrt(n);
for(int i = 1; i <= n; i++) id[i] = (i-1)/t2+1;
for(int i = 1; i <= id[n]; i++) L[i] = (i-1)*t2+1, R[i] = i*t2;
R[id[n]] = n;
sort(b+1, b+n+1);
n2 = unique(b+1, b+n+1) - b - 1;
for(int i = 1; i <= n; i++) a[i] = lower_bound(b+1, b+n2+1, a[i]) - b;
num = id[n];
for(int i = 1; i <= num; i++){
for(int j = L[i]; j <= R[i]; j++) s[i][a[j]]++;
for(int j = 1; j <= n2; j++) s[i][j] += s[i-1][j];
}
for(int i = 1; i <= num; i++){
for(int j = i; j <= num; j++){
int ans = f[i][j-1];
for(int k = L[j]; k <= R[j]; k++){
if(vis[a[k]]) continue;
if((s[j][a[k]] - s[i-1][a[k]]) % 2 == 0 and (s[j-1][a[k]] - s[i-1][a[k]]) % 2 == 1 and (s[j][a[k]] - s[i-1][a[k]]) > 0 and (s[j-1][a[k]] - s[i-1][a[k]]) > 0) ans++;
if((s[j][a[k]] - s[i-1][a[k]]) % 2 == 1 and (s[j-1][a[k]] - s[i-1][a[k]]) % 2 == 0 and (s[j][a[k]] - s[i-1][a[k]]) > 0 and (s[j-1][a[k]] - s[i-1][a[k]]) > 0) ans--;
if((s[j][a[k]] - s[i-1][a[k]]) % 2 == 0 and (s[j-1][a[k]] - s[i-1][a[k]]) == 0 and (s[j][a[k]] - s[i-1][a[k]]) > 0) ans++;
vis[a[k]]=1;
}
for(int k = L[j]; k <= R[j]; k++) vis[a[k]] = 0;
f[i][j] = ans;
}
}
int last = 0;
for(int i = 1; i <= m; i++){
int l = ((read() + last) % n) + 1, r = ((read() + last) % n) + 1;
if(l > r) swap(l, r);
int ans = query(l, r);
write(ans);
last = ans;
puts("");
}
return 0;
}
- P5048 [Ynoi2019 模拟赛] Yuno loves sqrt technology III 更优美的求区间众数
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
static char buf[1000000],*p1=buf,*p2=buf;
#define getchar() p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++
inline int read(){int x=0,f=1;char c=getchar();while(c<'0' || c>'9'){if(c=='-') f=-1;c=getchar();}while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+c-48;c=getchar();}return x*f;}
inline void write(int x){static char buf[20];static int len=-1;if(x<0)putchar('-'),x=-x;do buf[++len]=x%10,x/=10;while(x);while(len>=0)putchar(buf[len--]+48);}
const int MAX = 500005;
const int MAX2 = 720;
int n, m;
int n2, num, t2;
int a[MAX], b[MAX];
int id[MAX], L[MAX], R[MAX];
int f[MAX2][MAX2];
int cnt[MAX];
vector <int> v[MAX];
int pos[MAX];
int t[MAX];
int query(int l, int r){
int p = id[l], q = id[r];
int ans = 0;
int re = 0;
if(p == q){
for(int i = l; i <= r; i++) t[a[i]]++;
for(int i = l; i <= r; i++) if(t[a[i]] > t[ans] or (t[a[i]] == t[ans] and a[i] < ans)) ans = a[i];
re = t[ans];
for(int i = l; i <= r; i++) t[a[i]] = 0;
}else{
ans = f[p+1][q-1];
for(int i = l; i <= R[p]; i++){
int now = pos[i] + ans;
while(now < v[a[i]].size() and v[a[i]][now] <= r) ans++, now++;
}
for(int i = L[q]; i <= r; i++){
int now = pos[i] - ans;
while(now >= 0 and v[a[i]][now] >= l) ans++, now--;
}
re = ans;
}
return re;
}
signed main(){
n = read(), m = read();
for(int i = 1; i <= n; i++) b[i] = a[i] = read();
t2 = sqrt(n);
for(int i = 1; i <= n; i++) id[i] = (i-1)/t2+1;
for(int i = 1; i <= id[n]; i++) L[i] = (i-1)*t2+1, R[i] = i*t2;
R[id[n]] = n;
sort(b+1, b+n+1);
n2 = unique(b+1, b+n+1) - b - 1;
for(int i = 1; i <= n; i++) a[i] = lower_bound(b+1, b+n2+1, a[i]) - b, v[a[i]].push_back(i), pos[i] = v[a[i]].size()-1;
num = id[n];
for(int i = 1; i <= num; i++){
memset(cnt, 0, sizeof(cnt));
for(int j = i; j <= num; j++){
f[i][j] = f[i][j-1];
for(int k = L[j]; k <= R[j]; k++){
cnt[a[k]]++;
f[i][j] = max(f[i][j], cnt[a[k]]);
}
}
}
int last = 0;
for(int i = 1; i <= m; i++){
int l = read() xor last, r = read() xor last;
if(l > r) swap(l, r);
int ans = query(l, r);
write(ans);
last = ans;
puts("");
}
return 0;
}
- P5356 [Ynoi2017] 由乃打扑克 -> 题解https://www.cnblogs.com/WRuperD/p/16725324.html


