可持久化数据结构
可持久化数据结构
前置知识:
能熟练掌握基本数据结构,如Trie,线段树。
什么是可持久化?
持久化是将程序数据在持久状态和瞬时状态间转换的机制。通俗的讲,就是瞬时数据(比如内存中的数据,是不能永久保存的)持久化为持久数据(比如持久化至数据库中,能够长久保存)——baidu百科
通俗来讲,可持久化就是指一个数据结构能查询历史记录。
主席树
朴素方法
容易想到,朴素的方法就是对于每一次修改都全部备份一次数据。已线段树为例,这样子单次修改的复杂度就变为了\(O(n)\),保障不了时间复杂度,且空间复杂度也不在可接受的范围之内。
实现
下图来源于oi-wiki
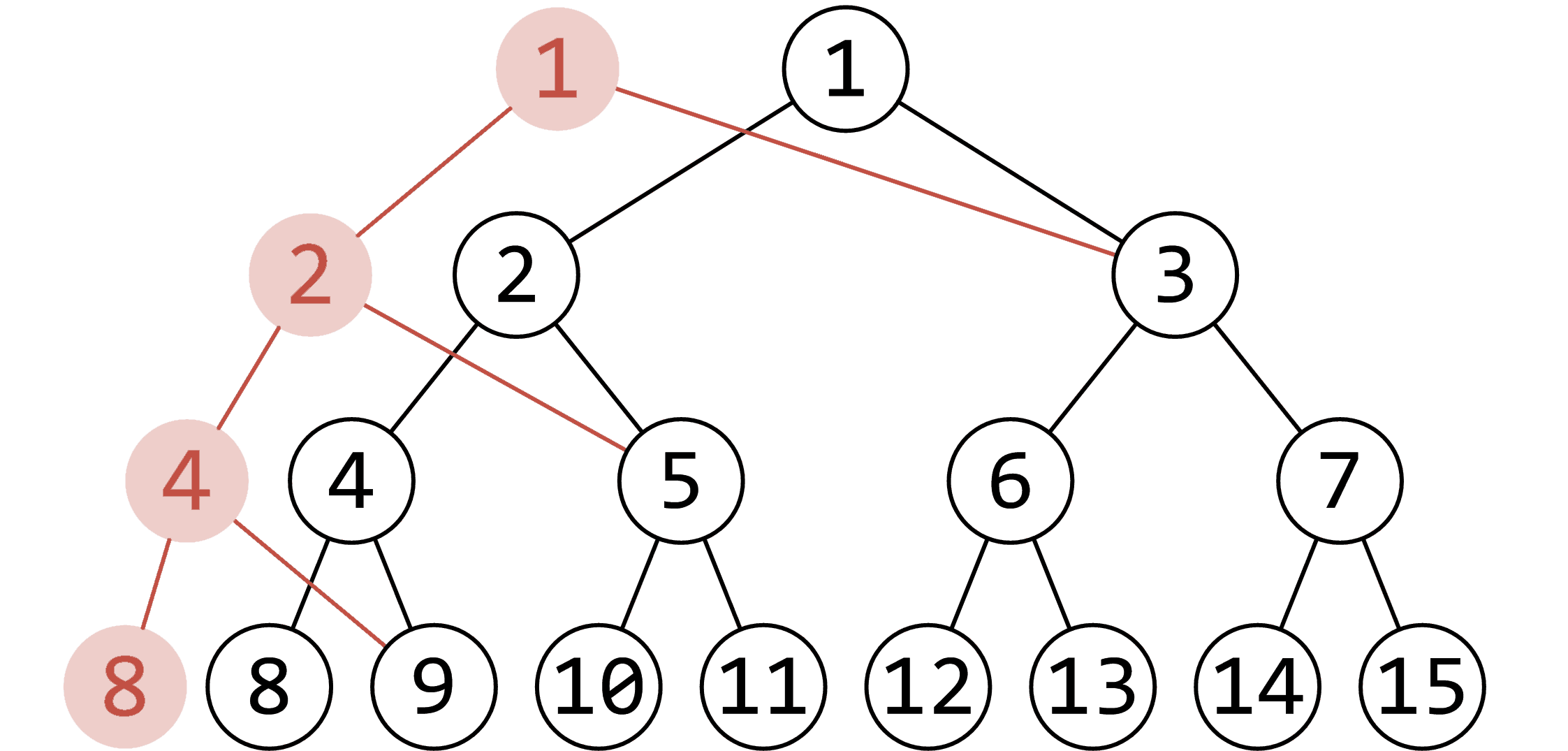
我们队上面的方法稍微优化一下。我们可以发现,就像线段树的懒标记一样,对于每次修改,我们不必记录下所有的节点的备份,我们只需要对于变化的节点进行备份即可。对于每次操作,我们最多只需要修改\(O(logn)\)个节点。所以可持久化线段树的复杂度依然查询可插入都是\(O(logn)\),空间复杂度约为\(O(qlogn)\)。那么,到底怎样记录备份呢?如图,我们只需要在树上再开一个新节点便可以记录备份。因此,我们要摒弃传统的堆式存储二叉树的方式,而改为存储节点的权值和每个节点的对应的左右儿子(函数式线段树)。
「模板」可持久化线段树
题目描述
线段树有个非常经典的应用是处理RMQ问题,即区间最大/最小值询问问题。现在我们把这个问题可持久化一下:
Q k l r 查询数列在第k个版本时,区间[l, r]上的最大值
M k p v 把数列在第k个版本时的第p个数修改为v,并产生一个新的数列版本
最开始会给你一个数列,作为第1个版本。每次M操作会导致产生一个新的版本。
输入格式
第一行两个整数N, Q。N是数列的长度,Q表示询问数
第二行N个整数,是这个数列
之后Q行,每行以0或者1开头,0表示查询操作Q,1表示修改操作M,格式为
0 k l r 查询数列在第k个版本时,区间[l, r]上的最大值 或者
1 k p v 把数列在第k个版本时的第p个数修改为v,并产生一个新的数列版本
样例输入
4 5
1 2 3 4
0 1 1 4
1 1 3 5
0 2 1 3
0 2 4 4
0 1 2 4
样例输出
4
5
4
4
代码:
#include<iostream>
using namespace std;
const int A = 100005;
int n, m;
int a[A];
int lc[20*A], rc[20*A], val[20*A];//左儿子,右儿子编号,点权值
int root[A], ver;//每个版本的根节点和版本号
int psz;//最大点编号
void push_up(int x){
val[x] = max(val[rc[x]], val[lc[x]]);//注意这里不是2*x和2*x+1
}
int build(int l, int r)
{
int o = psz++;// 当前节点编号
if(l==r)
{
val[o] = a[l];
return o;//返回当前节点编号
}
int mid = (l+r)/2;
lc[o] = build(l,mid);//记得给左儿子赋值
rc[o] = build(mid+1,r);//记得给右儿子赋值
push_up(o);
return o;
}
int upd(int p, int jia, int l, int r, int x)
{
int o = psz++;
val[o] = val[x], lc[o] = lc[x], rc[o] = rc[x];//创建备份
if(l==r)
{
val[o] = jia; return o;//返回节点编号
}
int mid = (l+r)/2;
if(p <= mid) lc[o] = upd(p,jia,l, mid, lc[o]);//这里需要注意左右儿子的编号不要习惯性写成堆式结构
else rc[o] = upd(p,jia,mid+1,r,rc[o]);
push_up(o);
return o;//返回节点编号
}
int Q(int L, int R, int l, int r, int rt)
{
if(l >= L and r <= R)
{
return val[rt];
}
int mid = (l+r)/2;
int ans = 0;
if(L <= mid) ans = Q(L,R,l,mid,lc[rt]);
if(R > mid) ans = max(ans, Q(L,R,mid+1,r,rc[rt]));
return ans;
}
int main()
{
cin>>n>>m;
for(int i = 1; i <= n; i++) cin>>a[i];
root[ver=1] = build(1, n); //给第一个版本服更节点
for(int i = 1; i <= m; i++)
{
int t;
cin>>t;
if(t==1){
int k, p, v;
cin>>k>>p>>v;
root[++ver] = upd(p,v,1,n,root[k]);//记得更新版本更节点
}
else{
int k, x, y;
cin>>k>>x>>y;
cout<<Q(x,y,1,n,root[k])<<endl;//由那个版本跟节点往下搜
}
}
return 0;
}
据此,我们便可以实现可持久化数组(luogu P3919)
点击查看代码
#include<iostream>
using namespace std;
#define endl '\n'
const int A = 1000005;
int n, m;
int a[A];
int lc[24*A], rc[24*A], val[24*A];//左儿子,右儿子编号,点权值
int root[A], ver;//每个版本的根节点和版本号
int psz;//最大点编号
void push_up(int x){
val[x] = val[rc[x]] + val[lc[x]];//注意这里不是2*x和2*x+1
}
int build(int l, int r)
{
int o = psz++;// 当前节点编号
if(l==r)
{
val[o] = a[l];
return o;//返回当前节点编号
}
int mid = (l+r)/2;
lc[o] = build(l,mid);//记得给左儿子赋值
rc[o] = build(mid+1,r);//记得给右儿子赋值
push_up(o);
return o;
}
int upd(int p, int jia, int l, int r, int x)
{
int o = psz++;
val[o] = val[x], lc[o] = lc[x], rc[o] = rc[x];//创建备份
if(l==r)
{
val[o] = jia; return o;//返回节点编号
}
int mid = (l+r)/2;
if(p <= mid) lc[o] = upd(p,jia,l, mid, lc[o]);//这里需要注意左右儿子的编号不要习惯性写成堆式结构
else rc[o] = upd(p,jia,mid+1,r,rc[o]);
push_up(o);
return o;//返回节点编号
}
int Q(int L, int R, int l, int r, int rt)
{
if(l >= L and r <= R)
{
return val[rt];
}
int mid = (l+r)/2;
int ans = 0;
if(L <= mid) ans = Q(L,R,l,mid,lc[rt]);
if(R > mid) ans += Q(L,R,mid+1,r,rc[rt]);
return ans;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
for(int i = 1; i <= n; i++) cin>>a[i];
root[ver=0] = build(1, n); //给第一个版本服更节点
for(int i = 1; i <= m; i++)
{
int k, t;
cin>>k>>t;
if(t == 1){
int p, v;
cin>>p>>v;
root[++ver] = upd(p, v, 1, n, root[k]);
}else{
int x;
cin>>x;
cout<<Q(x, x, 1, n, root[k])<<endl;
root[++ver] = root[k];
}
}
return 0;
}
可持久化线段树也有一个好听的名字叫做主席树
静态区间kth
静态区间第k小是主席树的经典应用。
来看题目:
link
这里只简单讲讲思路:我们这里将值域线段树可持久化,维护1-i中数字在[x, y]范围内的个数。
来看AC代码:
#include<bits/stdc++.h>
using namespace std;
const int A = 200005;
int n, m;
int a[A];
int lc[25*A], rc[25*A], val[25*A];//左儿子,右儿子编号,点权值
int b[A];
int root[A], ver;//每个版本的根节点和版本号
int psz;//最大点编号
int build(int l, int r)
{
int o = ++psz;// 当前节点编号
if(l==r)
{
return o;//返回当前节点编号
}
int mid = (l+r)/2;
lc[o] = build(l,mid);//记得给左儿子赋值
rc[o] = build(mid+1,r);//记得给右儿子赋值
// push_up(o);
return o;
}
int upd(int p, int l, int r, int x)
{
int o = ++psz;
val[o] = val[x]+1, lc[o] = lc[x], rc[o] = rc[x];//创建备份
if(l==r)
{
return o;//返回节点编号
}
int mid = (l+r)/2;
if(p <= mid) lc[o] = upd(p,l, mid, lc[o]);//这里需要注意左右儿子的编号不要习惯性写成堆式结构
else rc[o] = upd(p,mid+1,r,rc[o]);
return o;//返回节点编号
}
int Q(int u, int v, int l, int r, int rt)
{
int ans, mid = (l+r)/2, x = val[lc[v]] - val[lc[u]];
if(l == r) return l;
if(x >= rt) ans = Q(lc[u], lc[v], l, mid, rt);
else ans = Q(rc[u], rc[v], mid+1, r, rt - x);
return ans;
}
int main()
{
// freopen("ccs.out", "w", stdout);
cin>>n>>m;
for(int i = 1; i <= n; i++) cin>>a[i], b[i] = a[i];
sort(b+1, b+n+1);
int n2 = unique(b+1, b+n+1) - b - 1;
root[0] = build(1, n2); //给第一个版本服更节点
for(int i = 1; i <= n; i++){
int p = lower_bound(b+1, b+n2+1, a[i]) - b;
root[i] = upd(p, 1, n2, root[i-1]);
}
for(int i = 1; i <= m; i++)
{
int l, r, k;
cin>>l>>r>>k;
int ans = Q(root[l-1], root[r], 1, n2, k);
cout<<b[ans]<<endl;
}
return 0;
}
更详细的可以见这位大佬的博客。




