实现strStr()函数
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
示例1:
输入: haystack = "hello", needle = "ll"
输出: 2
示例2:
输入:haystack = "aaaaa", needle = "bba"
输出:-1
说明:
当needle是空字符串时,应当返回什么值呢?
对于本题而言,当needle是空字符串时应当返回0。这与C语言的strstr()以及Java的indexOf()定义相符合。
子串逐一比较的解法最简单,将长度为 L 的滑动窗口沿着 haystack 字符串逐步移动,并将窗口内的子串与 needle 字符串相比较,时间复杂度为 O((N - L)L)O((N−L)L)
显然上面这个方法是可以优化的;双指针方法虽然也是线性时间复杂度,不过它可以避免比较所有的子串,因此最优情况下的时间复杂度为 O(N)O(N),但最坏情况下的时间复杂度依然为 O((N - L)L)O((N−L)L)。
有 O(N)O(N) 复杂度的解法嘛?答案是有的,有两种方法可以实现:
- Rabin-Karp,通过哈希算法实现常数时间窗口内字符串比较。
- 比特位操作,通过比特掩码来实现常数时间窗口内字符串比较。
方法一、子串逐一比较-线性时间复杂度
最直接的方法 - 沿着字符串逐步移动滑动窗口,将窗口内的子串与 needle 字符串比较。
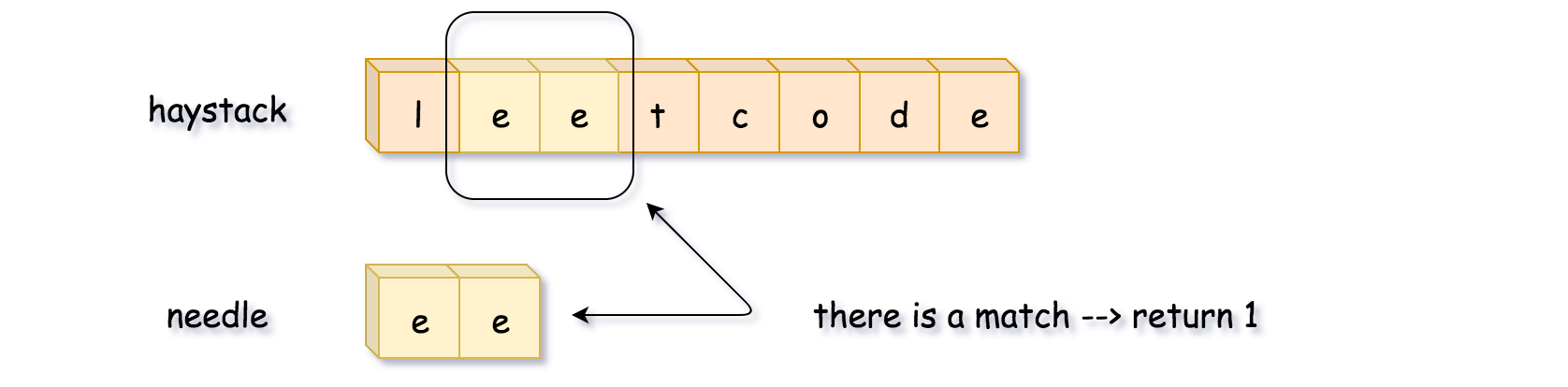
实现:
Python:
1 class Solution: 2 def strStr(self, haystack: str, needle: str) -> int: 3 L, n = len(needle), len(haystack) 4 5 for start in range(n - L + 1): 6 if haystack[start: start + L] == needle: 7 return start 8 return -1
Java:
1 class Solution { 2 public int strStr(String haystack, String needle) { 3 int L = needle.length(), n = haystack.length(); 4 5 for (int start = 0; start < n - L + 1; ++start) { 6 if (haystack.substring(start, start + L).equals(needle)) { 7 return start; 8 } 9 } 10 return -1; 11 } 12 }
复杂度分析:
- 时间复杂度:O((N - L)L),其中 N 为 haystack 字符串的长度,L 为 needle 字符串的长度。内循环中比较字符串的复杂度为 L,总共需要比较 (N - L) 次。
- 空间复杂度:O(1)。
方法二、双指针-线性时间复杂度
方法一的缺陷是会将haystack 所有长度为 L 的子串都与 needle 字符串比较,实际上是不需要这么做的。首先,只有子串的第一个字符跟 needle 字符串第一个字符相同的时候才需要比较。
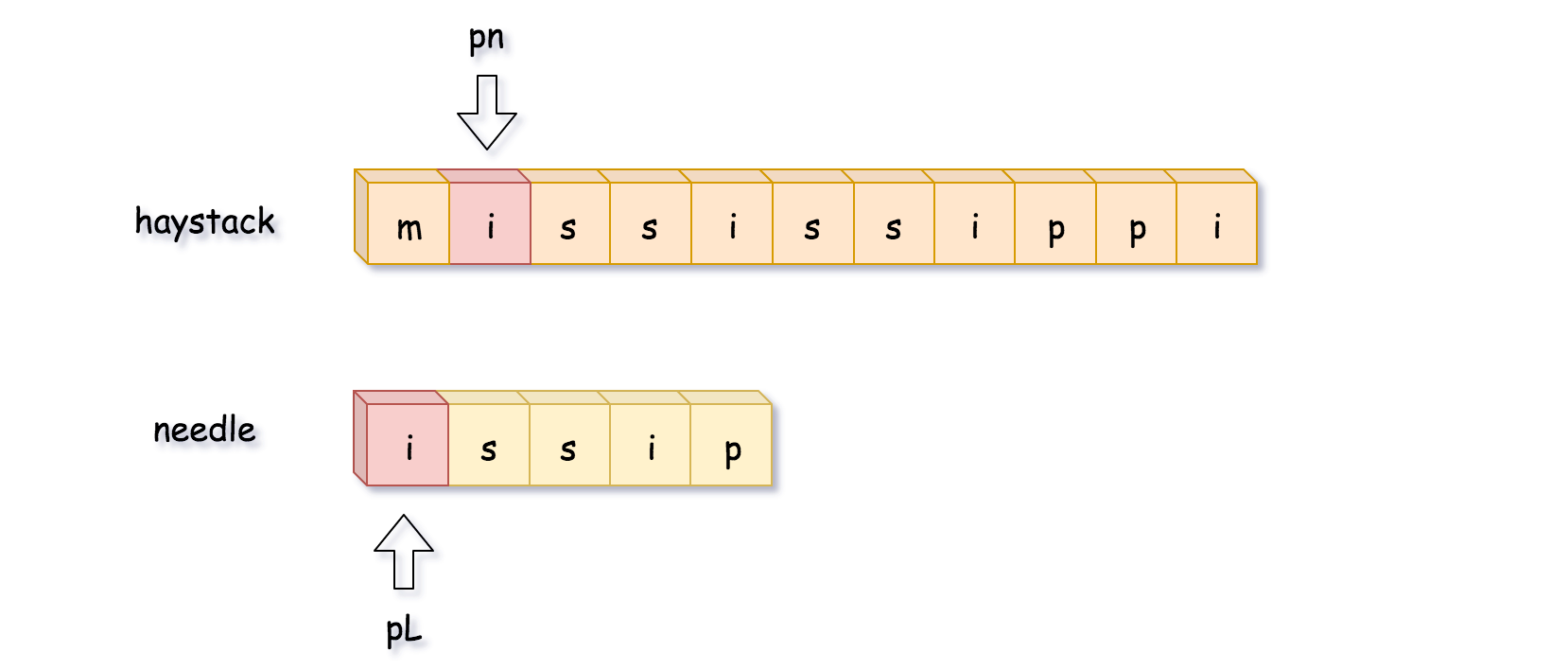
其次,可以一个字符一个字符比较,一旦不匹配就立刻终止。
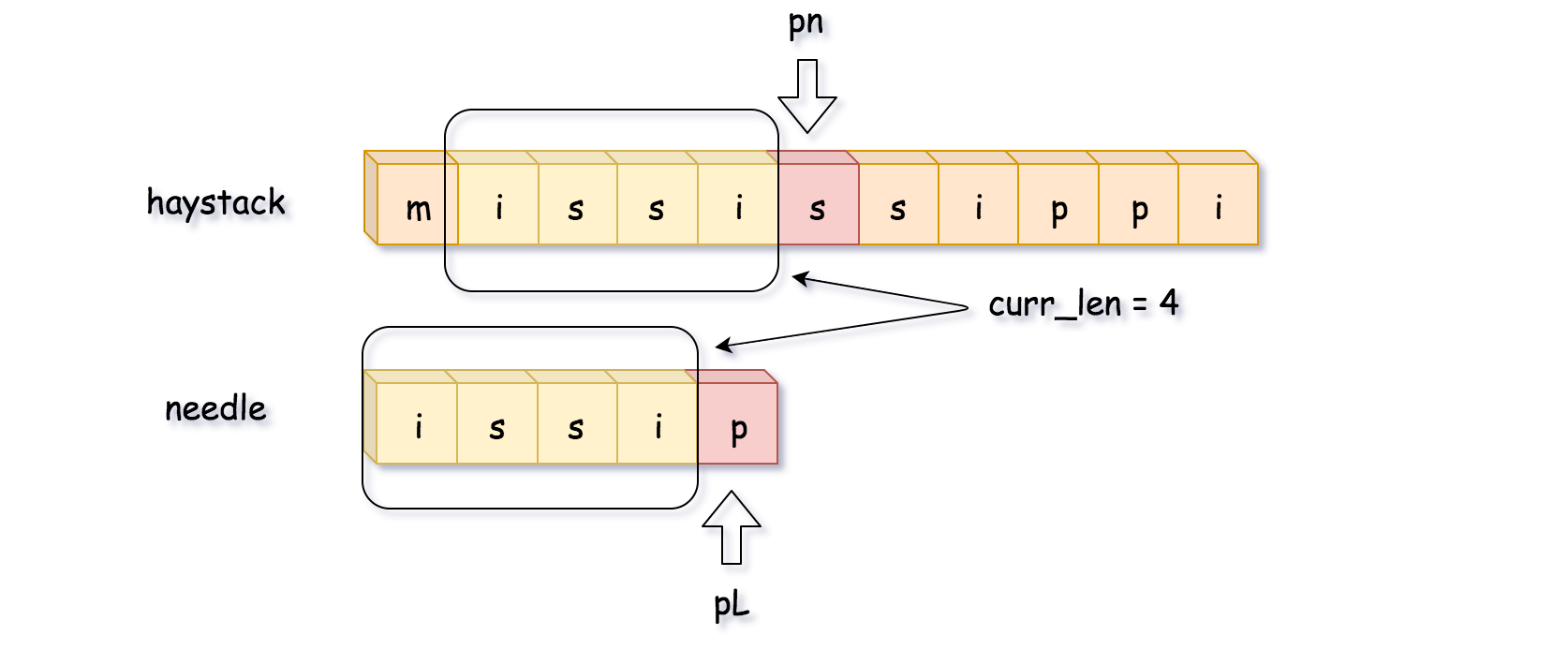
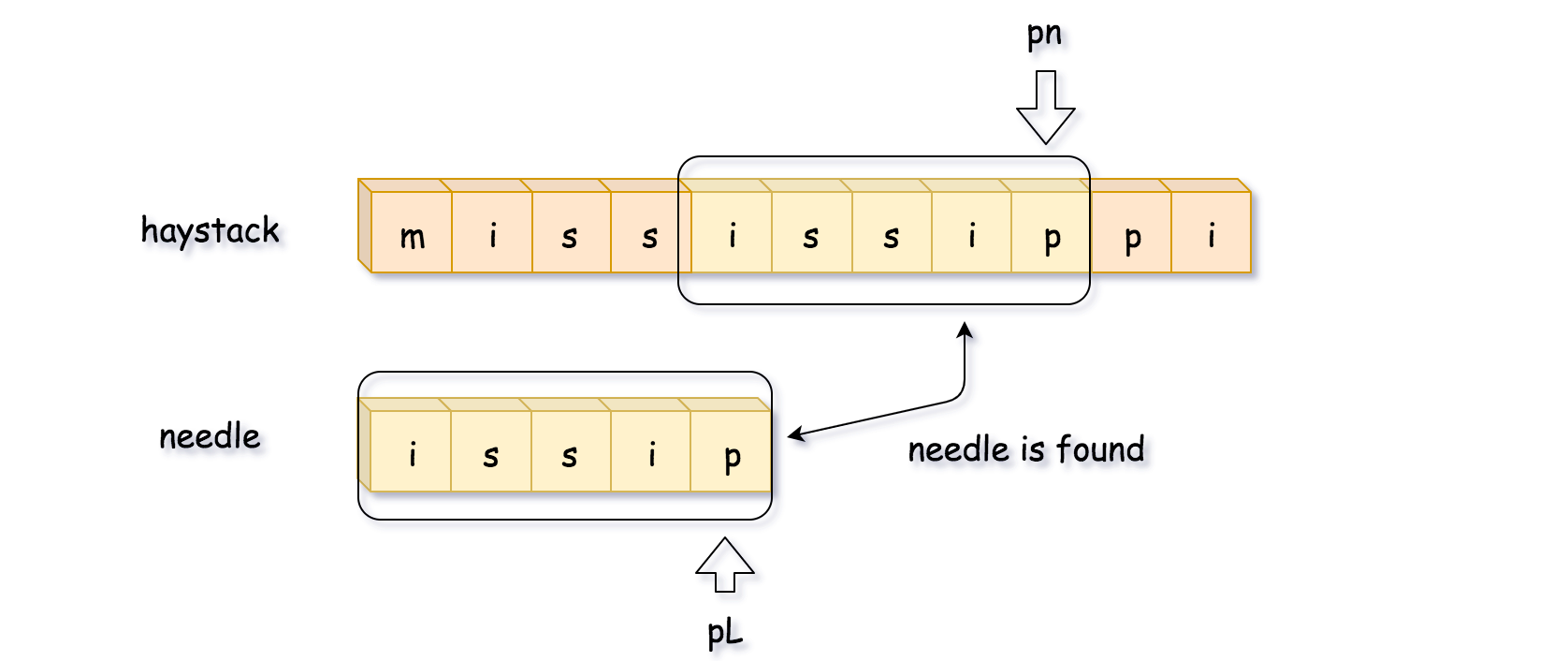
如下图所示,比较到最后一位时发现不匹配,这时候开始回溯。需要注意的是,pn 指针是移动到 pn = pn - curr_len + 1 的位置,而 不是 pn = pn - curr_len 的位置。
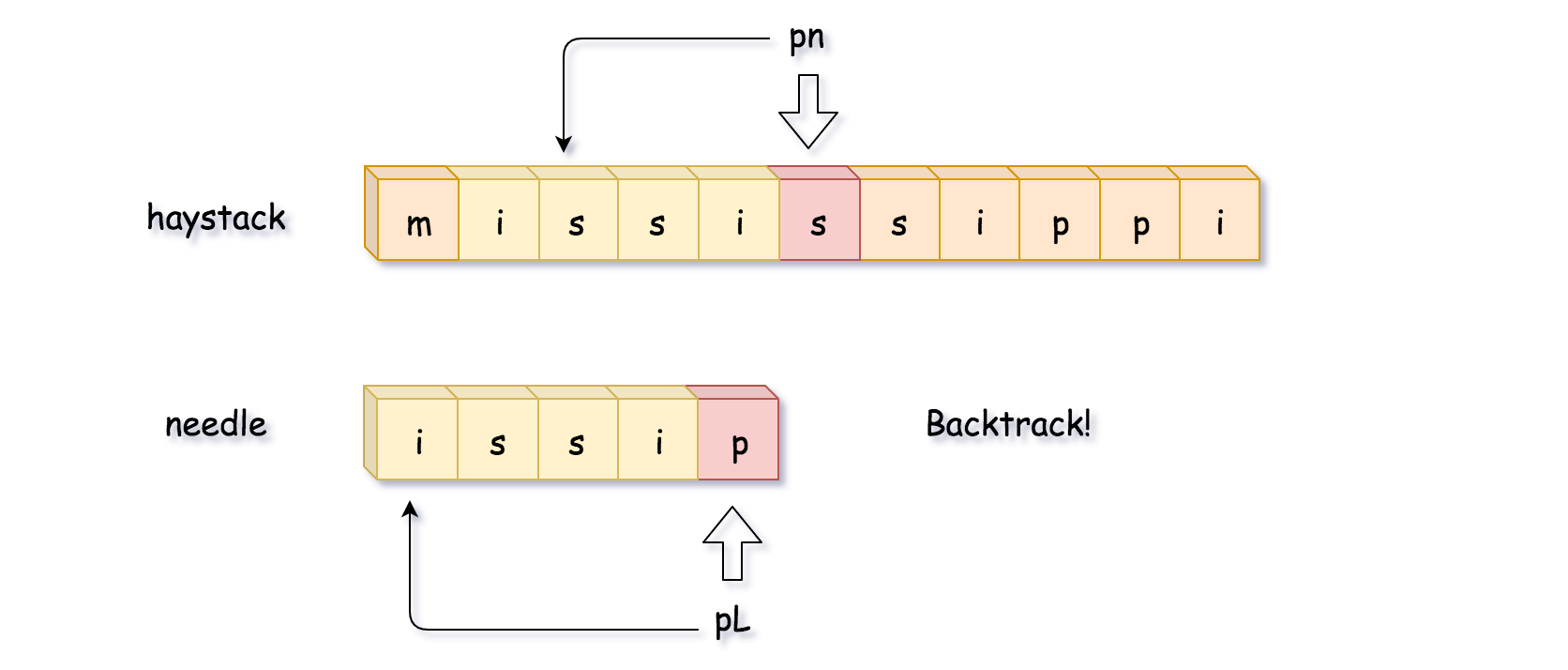
再比较一次,就找到了完整匹配的子串,直接返回子串的开始位置 pn - L。
算法:
- 移动 pn 指针,直到 pn 所指向位置的字符与 needle 字符串第一个字符相等
- 通过 pn,pL,curr_len 计算匹配长度
- 如果完全匹配(即 curr_len == L),返回匹配子串的起始坐标(即 pn - L)
- 如果不完全匹配,回溯。使 pn = pn - curr_len + 1, pL = 0, curr_len = 0
实现:
Python:
1 class Solution: 2 def strStr(self, haystack: str, needle: str) -> int: 3 L, n = len(needle), len(haystack) 4 if L == 0: 5 return 0 6 7 pn = 0 8 while pn < n - L + 1: 9 # find the position of the first needle character 10 # in the haystack string 11 while pn < n - L + 1 and haystack[pn] != needle[0]: 12 pn += 1 13 14 # compute the max match string 15 curr_len = pL = 0 16 while pL < L and pn < n and haystack[pn] == needle[pL]: 17 pn += 1 18 pL += 1 19 curr_len += 1 20 21 # if the whole needle string is found, 22 # return its start position 23 if curr_len == L: 24 return pn - L 25 26 # otherwise, backtrack 27 pn = pn - curr_len + 1 28 29 return -1
Java:
1 class Solution { 2 public int strStr(String haystack, String needle) { 3 int L = needle.length(), n = haystack.length(); 4 if (L == 0) return 0; 5 6 int pn = 0; 7 while (pn < n - L + 1) { 8 // find the position of the first needle character 9 // in the haystack string 10 while (pn < n - L + 1 && haystack.charAt(pn) != needle.charAt(0)) ++pn; 11 12 // compute the max match string 13 int currLen = 0, pL = 0; 14 while (pL < L && pn < n && haystack.charAt(pn) == needle.charAt(pL)) { 15 ++pn; 16 ++pL; 17 ++currLen; 18 } 19 20 // if the whole needle string is found, 21 // return its start position 22 if (currLen == L) return pn - L; 23 24 // otherwise, backtrack 25 pn = pn - currLen + 1; 26 } 27 return -1; 28 } 29 }
复杂度分析:
- 时间复杂度:最坏时间复杂度为 O((N - L)L),最优时间复杂度为 O(N)。
- 空间复杂度:O(1)。
方法三、Rabin Karp - 常数复杂度
有一种最坏时间复杂度也为 O(N)的算法。思路是这样的,首先生成窗口内子串的哈希码,然后再跟 needle 字符串的哈希码做比较。
这个思路有一个问题需要解决,如何在常数时间生成子串的哈希码?
滚动哈希:常数时间生成哈希码
生成一个长度为 L 数组的哈希码,需要 O(L)O(L) 时间。
如何在常数时间生成滑动窗口数组的哈希码?利用滑动窗口的特性,每次滑动都有一个元素进,一个出。
由于只会出现小写的英文字母,因此可以将字符串转化成值为 0 到 25 的整数数组: arr[i] = (int)S.charAt(i) - (int)'a'。按照这种规则,abcd 整数数组形式就是 [0, 1, 2, 3],转换公式如下所示:
h0 = 0 × 263 + 1 × 262 + 2 × 261 + 3 × 260
可以将上面的公式写成通式,如下所示(其中 ci 为整数数组中的元素,a = 26,其为字符集的个数):
h0 = c0aL-1 + c1aL-2 + ··· + ciaL-1-i + ··· + cL-1a1 + cLa0
h0 = ∑ciaL-1-i (0 ≤ i < L)
下面来考虑窗口从 abcd 滑动到 bcde 的情况。这时候整数形式数组从 [0, 1, 2, 3] 变成了 [1, 2, 3, 4],数组最左边的 0 被移除,同时最右边新添了 4。滑动后数组的哈希值可以根据滑动前数组的哈希值来计算,计算公式如下所示:
h1 = (h0 - 0 × 263) × 26 + 4 × 260
写成通式如下所示:
h1 = (h0a - c0aL) + cL+1
如何避免溢出
aL可能是一个很大的数字,因此需要设置数值上限来避免溢出。设置数值上限可以用取模的方式,即用 h % modulus 来代替原本的哈希值。
理论上,modules 应该取一个很大数,但具体应该取多大的数呢? 对于这个问题来说231就足够了。
算法:
- 计算子字符串 haystack.substring(0, L) 和 needle.substring(0, L) 的哈希值
- 从起始位置开始遍历:从第一个字符遍历到第 N - L 个字符
- 根据前一个哈希值计算滚动哈希
- 如果子字符串哈希值与 needle 字符串哈希值相等,返回滑动窗口起始位置
- 返回 -1,这时候 haystack 字符串中不存在 needle 字符串
实现:
Python:
1 class Solution: 2 def strStr(self, haystack: str, needle: str) -> int: 3 L, n = len(needle), len(haystack) 4 if L > n: 5 return -1 6 7 # base value for the rolling hash function 8 a = 26 9 # modulus value for the rolling hash function to avoid overflow 10 modulus = 2**31 11 12 # lambda-function to convert character to integer 13 h_to_int = lambda i : ord(haystack[i]) - ord('a') 14 needle_to_int = lambda i : ord(needle[i]) - ord('a') 15 16 # compute the hash of strings haystack[:L], needle[:L] 17 h = ref_h = 0 18 for i in range(L): 19 h = (h * a + h_to_int(i)) % modulus 20 ref_h = (ref_h * a + needle_to_int(i)) % modulus 21 if h == ref_h: 22 return 0 23 24 # const value to be used often : a**L % modulus 25 aL = pow(a, L, modulus) 26 for start in range(1, n - L + 1): 27 # compute rolling hash in O(1) time 28 h = (h * a - h_to_int(start - 1) * aL + h_to_int(start + L - 1)) % modulus 29 if h == ref_h: 30 return start 31 32 return -1
Java:
1 class Solution { 2 // function to convert character to integer 3 public int charToInt(int idx, String s) { 4 return (int)s.charAt(idx) - (int)'a'; 5 } 6 7 public int strStr(String haystack, String needle) { 8 int L = needle.length(), n = haystack.length(); 9 if (L > n) return -1; 10 11 // base value for the rolling hash function 12 int a = 26; 13 // modulus value for the rolling hash function to avoid overflow 14 long modulus = (long)Math.pow(2, 31); 15 16 // compute the hash of strings haystack[:L], needle[:L] 17 long h = 0, ref_h = 0; 18 for (int i = 0; i < L; ++i) { 19 h = (h * a + charToInt(i, haystack)) % modulus; 20 ref_h = (ref_h * a + charToInt(i, needle)) % modulus; 21 } 22 if (h == ref_h) return 0; 23 24 // const value to be used often : a**L % modulus 25 long aL = 1; 26 for (int i = 1; i <= L; ++i) aL = (aL * a) % modulus; 27 28 for (int start = 1; start < n - L + 1; ++start) { 29 // compute rolling hash in O(1) time 30 h = (h * a - charToInt(start - 1, haystack) * aL 31 + charToInt(start + L - 1, haystack)) % modulus; 32 if (h == ref_h) return start; 33 } 34 return -1; 35 } 36 }
复杂度分析:
- 时间复杂度:O(N),计算 needle 字符串的哈希值需要 O(L) 时间,之后需要执行 (N - L)次循环,每次循环的计算复杂度为常数。
- 空间复杂度:O(1)。



