位运算专题

LeetCode 231:给定一个整数，编写一个函数来判断它是否是 2 的幂次方。

示例 1:

输入: 1
输出: true
解释: 20 = 1

示例 2:

输入: 16
输出: true
解释: 24 = 16

示例 3:

输入: 218
输出: false

方法一：

　　思路：此题判断该数字二进制中1的个数，如果非负，其中1的位数只有一位就一定是2的幂，否则就不为2的幂，所以可以采取一位一位的判断比较，但是这样就更慢，所以可以采取其他办法，即n&(n-1)一定可以消去右边第一个出现的1；

　　大家可以这样理解，不管对于n中最后一个一的位置如何比如为....1000...（N个）假设1的后面有N个0，对于该数字减一而言就变成了....01111....(N个)后面的0全部就因为借位变成了1，此时将两个数字相与就会把最后一个1之后（包括1）全部变成了0.所以我们消去一个1之后如果还有1 那么这个数一定不为0，所以只需要进行与运算之后判断是否为0即可。

class Solution 
{
public:
    bool isPowerOfTwo(int n) 
    {
        if(n<=0) return false;
        return (n&(n-1))==0;
    }
};

 方法二：

　　思路：整数最大的2的整数幂是2^30；该数对所有2的幂取余都为0；非0的就不是2的幂。这是一个取巧的方法。

class Solution 
{
public:
    bool isPowerOfTwo(int n) 
    {
        return n > 0 && (1<<30)%n == 0;
    }
};

方法三：

　　思路：计算机中整数x是原码存储的； -x是补码存储（原码取反加一）；可以用5去实验，做出5 & -5 ，然后找关系；

　　　　所以，计算可以得出，x & -x 等于x的二进制表示里面的最右边的那个1；因为2的幂中只会有一个1，所以有，x & -x == x；

　　　　如果x中1的个数是多个，所以有 x & -x < x。

　　计算机用补码表示负数，主要因为计算机只会加法运算，不会减法，所以这样表示是为了用加法实现减法功能。

class Solution 
{
public:
    bool isPowerOfTwo(int n)
    {
        return n > 0 && (n & -n) == n;
    }
};

LeetCode 762:

　　给定两个整数 L 和 R ，找到闭区间 [L, R] 范围内，计算置位位数为质数的整数个数。

　　（注意，计算置位代表二进制表示中1的个数。例如 21 的二进制表示 10101 有 3 个计算置位。还有，1 不是质数。）

示例 1:

输入: L = 6, R = 10
输出: 4
解释:
6 -> 110 (2 个计算置位，2 是质数)
7 -> 111 (3 个计算置位，3 是质数)
9 -> 1001 (2 个计算置位，2 是质数)
10-> 1010 (2 个计算置位，2 是质数)

示例 2:

输入: L = 10, R = 15
输出: 5
解释:
10 -> 1010 (2 个计算置位, 2 是质数)
11 -> 1011 (3 个计算置位, 3 是质数)
12 -> 1100 (2 个计算置位, 2 是质数)
13 -> 1101 (3 个计算置位, 3 是质数)
14 -> 1110 (3 个计算置位, 3 是质数)
15 -> 1111 (4 个计算置位, 4 不是质数)

注意:

L, R 是 L <= R 且在 [1, 10^6] 中的整数。
R - L 的最大值为 10000。

思路：

　　数据区间最大 10^6，是小于 2^20 的，所以先把20以内的质数表示出来；然后计算数据中有多少个1，判断其是不是质数即可。

class Solution
{
public:
    int countPrimeSetBits(int L, int R)
    {
        unordered_set<int> primes({2, 3, 5, 7, 11, 13, 17, 19});
        int res;
        for(int i = L; i <= R; i++)
        {
            int s = 0;
            for(int k = i; k; k >>= 1) s += k & 1;
            if(primes.count(s)) res++; //count() 用于查找primes中s的个数。
        }
        return res;
    }
};

LeetCode 136：只出现一次的数字I

　　给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。说明：你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,1]
输出: 1

示例 2:

输入: [4,1,2,1,2]
输出: 4

　　思路：a ^ a = 0;

　　　　　0 ^ a = a;

class Solution 
{
public:
    int singleNumber(vector<int>& nums)
    {
        int res = 0;
        for(auto x : nums) res ^= x;
        return res;
    }
};

LeetCode 476:

　　给定一个正整数，输出它的补数。补数是对该数的二进制表示取反。

注意:

　　给定的整数保证在32位带符号整数的范围内。你可以假定二进制数不包含前导零位。

示例 1:

输入: 5
输出: 2
解释: 5的二进制表示为101（没有前导零位），其补数为010。所以你需要输出2。

示例 2:

输入: 1
输出: 0
解释: 1的二进制表示为1（没有前导零位），其补数为0。所以你需要输出0。

方法一：　

　　假设a为1110 0101，b为1111 1111，a^b = 0001 1010是a的取反。也就是说二进制位数与num相同，且全为1的数tmp与num的抑或即为所求。

class Solution 
{
public:
    int findComplement(int num) 
    {
        int tmp = 1;
        while (tmp < num)
        {
            tmp <<= 1;
            tmp += 1;
        }
        return (tmp^num);
    }
};

方法二：

　　依次移位取非。

class Solution 
{
public:
    int findComplement(int num) 
    {
        int res = 0, t = 0;
        while(num)
        {
            res += !(num & 1) << t; // 这里一定是取 !，而不是取 ~. 因为！运算，0就是1,1就是0；而~运算，是所有位都取反。
            num >>= 1;
            t++;
        }
        return res;
    }
};

LeetCode 137: 只出现一次的数字II

　　给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现了三次。找出那个只出现了一次的元素。

说明：你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,3,2]
输出: 3

示例 2:

输入: [0,1,0,1,0,1,99]
输出: 99

方法一：（最优做法）

思路：(状态机的思路)（没太明白）

　　二进制下不考虑进位的加法：136 题中我们用到了异或运算。实际上，异或运算的含义是二进制下不考虑进位的加法，

　　　　即：0 ^ 0 = 0 + 0 = 0   0 ^ 0 = 0 + 0 = 0,

　　　　　　0 ^ 1 = 0 + 1 = 1  0 ^ 1 = 0 + 1 = 1,

　　　　　　1 ^ 0 = 1 + 0 = 1 1 ^ 0 = 1 + 0 = 1,

　　　　　　1 ^ 1 = 1 + 1 = 0  1 ^ 1 = 1 + 1 = 0（不进位）。

　　三进制下不考虑进位的加法：通过定义某种运算 #，使得 0 # 1 = 1，1 # 1 = 2，2 # 1 = 0。在此运算规则下，出现了 3 次的数字的二进制所有位全部抵消为 0，而留下只出现 1 次的数字二进制对应位为 1。

　　　　因此，在此运算规则下将整个 arr 中数字遍历加和，留下来的结果则为只出现 1 次的数字。

 

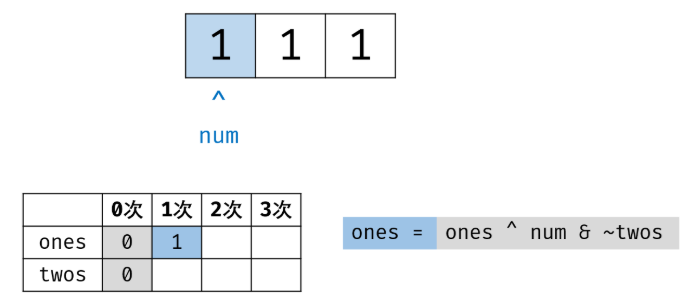
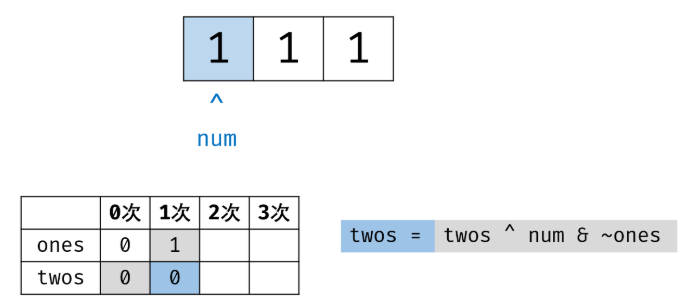
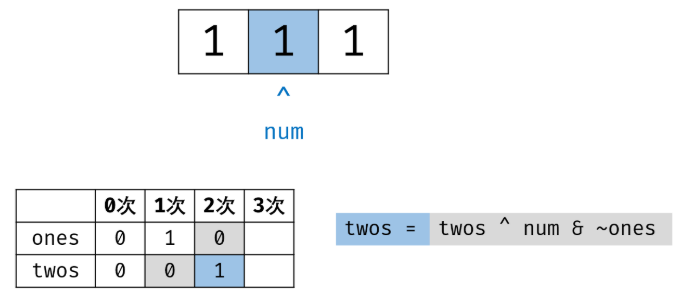
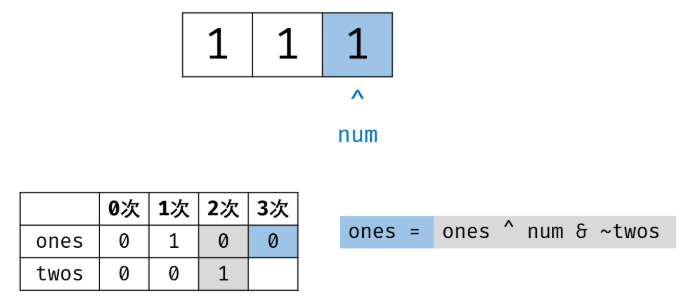
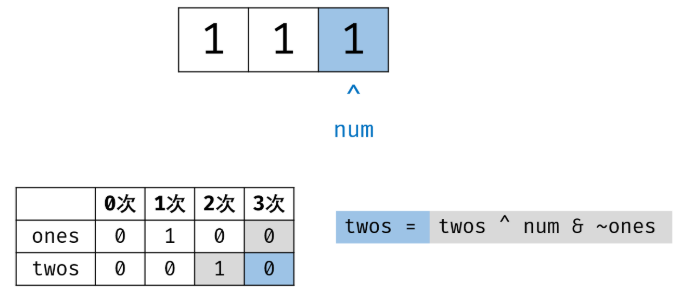
class Solution 
{
public:
    int singleNumber(vector<int>& nums)
    {
        int ones = 0, twos = 0;
        for(auto x : nums)
        {
            ones = (ones ^ x) & ~twos;
            twos = (twos ^ x) & ~ones;
        }
        return ones;
    }
};

 方法二：（一般做法）

 　　分别对所有数据的每一位进行对3取余操作。

class Solution 
{
public:
    int singleNumber(vector<int>& nums)
    {
        int ans = 0;
        for(int bit = 0; bit < 32; bit++)
        {
            int counter = 0;
            for(int i = 0; i < nums.size(); i++)
            {
                counter += (nums[i] >> bit) & 1;
            }
            
            ans += (counter % 3) << bit;
        }
        return ans;
    }
};

 LeetCode 260：只出现一次的数据III

　　给定一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。

示例 :

输入: [1,2,1,3,2,5]
输出: [3,5]
注意：结果输出的顺序并不重要，对于上面的例子， [5, 3] 也是正确答案。你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现？

 　　思路：

　　　　第一步：
　　　　　　把所有的元素进行异或操作，最终得到一个异或值。因为是不同的两个数字，所以这个值必定不为0；

　　　　第二步：
　　　　　　取异或值最后一个二进制位为1的数字作为mask，如果是1则表示两个数字在这一位上不同。

　　　　第三步：
　　　　　　分组，就可以找出两个数。

class Solution 
{
public:
    vector<int> singleNumber(vector<int>& nums) 
    {
        int s = 0;
        for(auto x : nums) s ^= x;
        
        int k = 0;
        while(!(s >> k & 1)) k++;
        
        int s2 = 0;
        for(int x : nums)
        {
            if(x >> k & 1)
                s2 ^= x;
        }
        /*
            s = a ^ b;
            s2 = a;
            s ^ s2 = a ^ b ^ a = b;
        */
        
        return {s2, s2 ^ s}; // vector<int> ({s2, s2 ^ s});
    }
};

 LeetCode 371:不使用运算符 + 和 - ​​​​​​​，计算两整数 ​​​​​​​a 、b ​​​​​​​之和。

示例 1:

输入: a = 1, b = 2
输出: 3

示例 2:

输入: a = -2, b = 3
输出: 1

 思路：a ^ b 是不进位加法；a & b 只有在相对应的位都为1的时候才为1，所以a & b 表示有进位的位；所以，结果等于 a ^ b + (a & b) << 1;

class Solution
{
public:
    int getSum(int a, int b)
    {
        if(!b) return a;
        int sum = a ^ b, carry = (unsigned int)(a & b) << 1; // 这里将a&b强转unsigned int，是因为有的不支持负数左移
        return getSum(sum, carry);
    }
};

 LeetCode 201：给定范围 [m, n]，其中 0 <= m <= n <= 2147483647，返回此范围内所有数字的按位与（包含 m, n 两端点）。2147483647 这个数是int的最大值。

示例 1: 

输入: [5,7]
输出: 4

示例 2:

输入: [0,1]
输出: 0

思路：

　　判断m、n是否相等，如果不相等，m+1会使m的二进制数末位进位，有进位说明m的末位肯定有0的情况，0与任何数相与皆得0，所以结果的末位肯定是0。

　　同理，不断右移1位进行比较，直到最终 m=n 时，说明找到了[m,n]这个范围内高位没有变化的数，左移相同位数得到的结果就是所求的值。

法一：

class Solution
{
public:
    int rangeBitwiseAnd(int m, int n)
    {
        int count = 0; // 统计移位次数
        while (m != n)
        {
            m >>= 1;
            n >>= 1;
            count++;
        }
        n <<= count;
        return n;
    }
};

法二：

class Solution 
{
public:
    int rangeBitwiseAnd(int m, int n) 
    {
        while(n>m) 
            n = n&(n-1);
        return n;
    }
};