K近邻实现

1 定义画图函数，用来可视化数据分布

（注：jupyternotebook来编写的代码）

import  matplotlib.pyplot as plt
import numpy as np

%config ZMQInteractiveShell.ast_node_interactivity='all'

def draw(X_train,y_train,X_new):
    # 正负实例点初始化
    X_po=np.zeros(X_train.shape[1])
    X_ne=np.zeros(X_train.shape[1])
    # 区分正、负实例点
    for i in range(y_train.shape[0]):
        if y_train[i]==1:
            X_po=np.vstack((X_po,X_train[i]))
        else:
            X_ne=np.vstack((X_ne,X_train[i]))
    # 实例点绘图
    plt.plot(X_po[1:,0],X_po[1:,1],"g*",label="1")
    plt.plot(X_ne[1:, 0], X_ne[1:, 1], "rx", label="-1")
    plt.plot(X_new[:, 0], X_new[:, 1], "bo", label="test_points")
    # 测试点坐标值标注
    for xy in zip(X_new[:, 0], X_new[:, 1]):
        plt.annotate("test{}".format(xy),xy)
    # 设置坐标轴
    plt.axis([0,10,0,10])
    plt.xlabel("x1")
    plt.ylabel("x2")
    # 显示图例
    plt.legend()
    # 显示图像
    plt.show()

 2 KNN实现

import numpy as np
from collections import Counter

class KNN:
    def __init__(self, X_train, y_train, k):
        # 所需要的参数初始化
        self.k = k
        self.X_train = X_train
        self.y_train = y_train
        
    def predict(self, X_new):
        # 计算欧式距离
        # np.linalg.norm() 表示求范数，ord = 2 表示求2阶范数
        # 得到的结果形式为：[(d0, 1), (d1, -1), ...]，其中d0和d1表示距离，1和-1表示标签
        dist_list = [(np.linalg.norm(X_new - self.X_train[i], ord = 2), self.y_train[i]) for i in range(self.X_train.shape[0])]
        # 对所有距离进行排序
        dist_list.sort(key = lambda x : x[0])
        # 取前k个最小距离对应的类型（也就是y值）
        y_list = [dist_list[i][-1] for i in range(self.k)]  # [-1, 1, 1 ,-1,...]
        # 对上述k个点的分类进行统计
        y_count = Counter(y_list).most_common()  # [(-1, 3), (1, 2)]
        return y_count[0][0]

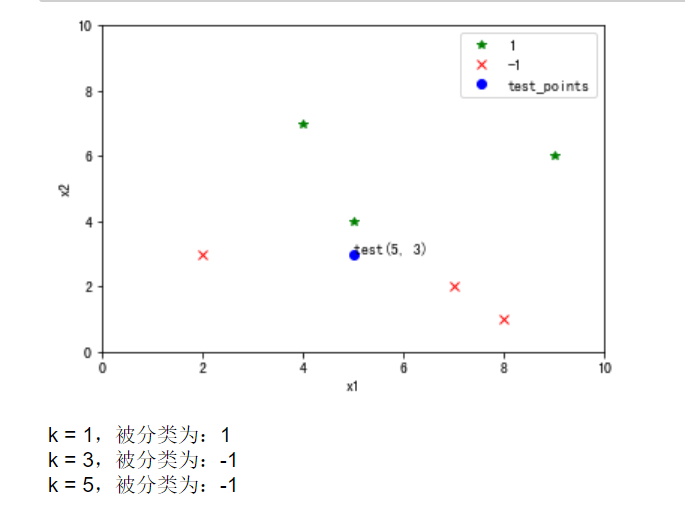
def main():
    # 训练数据集
    X_train = np.array([
        [5,4],
        [9,6],
        [4,7],
        [2,3],
        [8,1],
        [7,2]
    ])
    # 标签
    y_train = np.array([1,1,1,-1,-1,-1])
    # 测试数据
    X_new = np.array([[5, 3]])
    # 绘图
    draw(X_train, y_train, X_new)
    # k取不同值对分类结果的影响
    for k in range(1,6,2):  # 表示1-5每隔2个取一个数
        # 构建KNN实例
        clf = KNN(X_train, y_train, k=k)
        # 对测试数据进行分类预测
        y_predict = clf.predict(X_new)
        print('k = {}，被分类为：{}'.format(k, y_predict))

if __name__ == '__main__':
    main()

 

 3 运行结果