【2023.07.17】牛客&第四范式多校Day1（华中科技大学Round）过题小记

D - Chocolate（博弈论）

12分钟过题。签到。

K - Subdivision（图论、搜索）

1小时21分过题，签到。如果给定的是一棵树的话，新增的点一定位于连接叶子节点的那条边上、否则就是已有的点。然而这是一张图，所以我们可以使用 $\tt bfs$ 将其近似的转化为一棵树：当某个点（非其父节点）被第二次遍历到的时候，其就相当于叶子节点，当前点到这个点的边就是我们需要增加节点的边。

别忘了统计对已有的点是否满足条件。

J - Roulette（概率、暴力）

3小时28分过题，这道题卡这么久确实没想到。首先从这个数据范围看必然不能是直接暴力递推，于是考虑寻找关系。容易发现，无论何时赢得比赛，手里的钱均加且只加 $1$ ，而手里的钱的数量直接决定了你能输掉多少盘，于是，考虑对手里的钱的数量进行整数分块。

举例说明，当手里的钱为 $3,4,5,6$ 时，至多允许输掉一盘，于是组成的概率为 $[1]: $ 直接赢 $\dfrac{1}{2}$ 、$[2]: $ 输一盘后赢 $\dfrac{1}{2}^2$ ，随后手里的钱 $+1$ ；当手里的钱为 $7,8,\dots,14$ 时，至多允许输掉两盘，于是组成的概率为 $[1]: $ 直接赢 $\dfrac{1}{2}$ 、$[2]: $ 输一盘后赢 $\dfrac{1}{2}^2$ ，$[3]: $ 输两盘后赢 $\dfrac{1}{2}^3$ ，随后手里的钱 $+1$ 。

块的大小均为 $2$ 的倍数，最终复杂度 $\mathcal O(\log 10^9)$ 。

signed main() {
    int n, m;
    cin >> n >> m;
     
    int r;
    Z fac = Z(1) / 2, add = fac;
    for (int j = 4; ; j *= 2) {
        if (j - 1 > n) {
            r = j;
            break;
        }
        fac /= 2;
        add += fac;
    }
     
    Z ans = 1;
    for (int l = n; l <= n + m; ) {
        ans *= mypow(add, min(r - 2, n + m - 1) - l + 1);
        l = r - 1;
        r *= 2;
        fac /= 2;
        add += fac;
    }
    cout << ans << endl;
}

B - Anticomplementary Triangle（几何、贪心）

题意：平面上给定 $n\ (3\le n \le 10^6)$ 个点，保证这些点构成一个凸多边形，要求从中任选三个点使得这三个点构成的三角形的反互补三角形包含所有点（可以在边界）。通俗的说，构成的三角形是这个反互补三角形的中点三角形。

只过了十一个人的简单题。首先我们应当知道反互补三角形是怎么画出来的，即作边 $AB$ 过 $C$ 点的平行线、作边 $BC$ 过 $A$ 点的平行线、作边 $AC$ 过 $B$ 点的平行线。这三条件构成的三角形即为原三角形的反互补三角形。

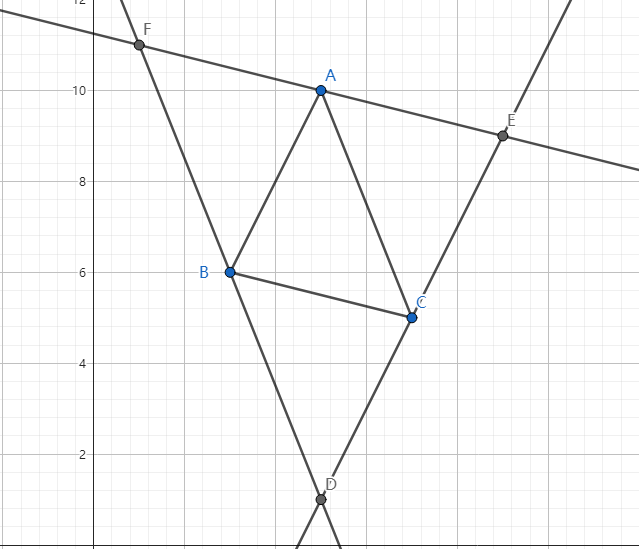
随后，本题的结论是，能被构成的全部三角形中面积最大的那个三角形一定满足条件。我们需要寻找一个算法使得其能够找到最大的三角形，这里选择的是比较典的暴力枚举试点。注意在计算面积时使用叉乘可以很好的避免浮点数精度不够的问题。本算法复杂度 $\mathcal O(n)$ ，注意到也有多一个 $\log$ 的做法，但是好像被卡了。

signed main() {
    int n;
    cin >> n;
     
    vector<point<int>> p(n);
    for (int i = 0; i < n; i++) {
        cin >> p[i].x >> p[i].y;
    }
     
    auto S = [&](int i, int j, int k) -> int {
        return cross(p[i] - p[j], p[k] - p[j]);
    };
     
    int i = 0, j = 1, k = 2;
    while (true) {
        int val = S(i, j, k);
        if (S((i + 1) % n, j, k) > val) {
            i = (i + 1) % n;
        } else if (S((i - 1 + n) % n, j, k) > val) {
            i = (i - 1 + n) % n;
        } else if (S(i, (j + 1) % n, k) > val) {
            j = (j + 1) % n;
        } else if (S(i, (j - 1 + n) % n, k) > val) {
            j = (j - 1 + n) % n;
        } else if (S(i, j, (k + 1) % n) > val) {
            k = (k + 1) % n;
        } else if (S(i, j, (k - 1 + n) % n) > val) {
            k = (k - 1 + n) % n;
        } else {
            break;
        }
    }
    cout << i + 1 << " " << j + 1 << " " << k + 1 << endl;
}

M - Water（数论、贪心）

题意：给定容量为 $A$ 和 $B$ 的两个杯子，问至少需要经过几次操作，使得一共可以喝到恰好 $x$ 单位的水；如果喝不到，输出 $-1$ 。

定义操作为：将杯子接满、将一个杯子中的水倒到另一个杯子里、将杯子中的水倒掉、喝掉杯子中的水。

题目情况很复杂（一共有四种），我们考虑如何恰好得到 $x$ ——化整为零发现 $x$ 其实只与 $A$ 和 $B$ 的系数相关，由裴蜀定律 $Aa+Bb=x\ (a,b \in Z^∗)$ 得到，如果能恰好喝到 $x$ 单位的水，那么 $\gcd(A, B)\mid x$ ，由此特判掉 $-1$ 的情况。

随后考虑如何构造，不妨设 $A\le B$ ，罗列四种情况如下（这四个情况对解出答案没有什么帮助）：

将 $A$ 装水后直接喝掉，$a$ 轮操作后喝掉 $a\cdot A$ ，花费 $2a$ 次操作；
将 $B$ 装水后直接喝掉，$b$ 轮操作后喝掉 $b\cdot B$ ，花费 $2b$ 次操作；
将 $B$ 装水后不停的倒入 $A$ ，然后倒掉 $A$ ，如果 $B$ 空了则再装水，如此往复，随时喝掉 $B$ 中剩下的；
将 $A$ 装水后倒入 $B$ ，如此往复，如果 $B$ 满了则倒掉，此时喝掉 $A$ 中剩下的。

仔细研究它们的关联后发现，最终答案聚焦于装了几次水/倒了几次水，联系到数学角度，即为求解 $a$ 和 $b$ 的正负符号，这样可以得出三种情况（这三个情况才是解题的关键）：

$a$ 和 $b$ 的符号均为正数（$(+,+)$，即用 $A$ 装 $a$ 次水、$B$ 装 $b$ 次水），此时操作次数即为 $2(a+b)$ ；
$a$ 和 $b$ 的符号为 $(+,-)$ （即用 $A$ 装 $a$ 次水、用 $B$ 倒掉 $b$ 次水），操作次数为 $2(a+|b|)-1$ ；
$a$ 和 $b$ 的符号为 $(-,+)$ ，操作次数为 $2(|a|+b)-1$ 。

注：这里画了绝对值是因为我个人觉得分离符号和值比较方便我理解；$-1$ 是因为喝掉的那一轮不需要再倒掉另一个杯子里的东西了，可以偷鸡一轮，如果还是不理解的话建议举几个例子验证一下。

剩下的就是找到 $\max \{2(a+b),2(|a|+|b|)-1\}$ 的答案了，这里用到扩展欧几里得解方程。

代码一：直接计算出正负最接近于 $0$ 的两个 $x$

int exgcd(int a, int b, int &x, int &y) {
    if (!b) {
        x = 1, y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}
signed main() {
    int Task = 1;
    for (cin >> Task; Task; Task--) {
        int a, b, c;
        cin >> a >> b >> c;
        
        if (a > b) {
            swap(a, b);
        }
        
        int x, y, d = exgcd(a, b, x, y), ans = 1e18;
        if (c % d) {
            cout << -1 << endl;
            continue;
        }
        
        int val = c / d; // 纠正值
        x *= val, y *= val; // 获得一组可行解
        
        a /= d, b /= d, c /= d;
        int t = x / b; // 偏移量
        
        x -= t * b, y += t * a; // 转化为 x 的绝对值最小的一组解
        if (x >= 0 && y >= 0) {
            ans = min(ans, 2 * (x + y));
        } else {
            ans = min(ans, 2 * abs(x) + 2 * abs(y) - 1);
        }
        
        if (x * b >= 0) x -= b, y += a; // 转化为 x 的绝对值最小的另一组解（符号相反）
        else x += b, y -= a;
        if (x >= 0 && y >= 0) {
            ans = min(ans, 2 * (x + y));
        } else {
            ans = min(ans, 2 * abs(x) + 2 * abs(y) - 1);
        }
        cout << ans << endl;
    }
}

代码二：暴力枚举找出全部解中最符合条件的那一组

int exgcd(int a, int b, int &x, int &y) {
    if (!b) {
        x = 1, y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}
signed main() {
    int Task = 1;
    for (cin >> Task; Task; Task--) {
        int a, b, c;
        cin >> a >> b >> c;
        
        if (a > b) {
            swap(a, b);
        }
        
        int x, y, d = exgcd(a, b, x, y), ans = 1e18;
        if (c % d) {
            cout << -1 << endl;
            continue;
        }
        
        int val = c / d; // 纠正值
        x *= val, y *= val; // 获得一组可行解
        
        a /= d, b /= d, c /= d;
        
        auto clac = [&](int t) -> void {
            int X = x + b * t, Y = y - a * t;
            if (X >= 0 && Y >= 0) {
                ans = min(ans, 2 * (X + Y));
            } else {
                ans = min(ans, 2 * abs(X) + 2 * abs(Y) - 1);
            }
        };
        
        // 附近找最小值
        int t = -x / b; // 偏移量，注意符号
        for (int i = t - 1; i <= t + 1; i++) clac(i);
        t = y / a;
        for (int i = t - 1; i <= t + 1; i++) clac(i);
        
        cout << ans << endl;
    }
}

A - Almost Correct（构造、暴力）

H - Matches（数据结构、贪心）

赛时队友说是二维数点。

inf.

posted @ 2023-07-17 23:44 hh2048 阅读(92) 评论(0) 编辑收藏举报

刷新页面返回顶部

hh2048

無限進步