【W的AC企划 - 第六期】位运算 (Bitmasks)
往期浏览
位运算
讲解
常见的位运算为:与、或、异或这三种。
| 运算 | 运算符、数学符号表示 | 解释 |
|---|---|---|
| 与 | &、and |
同1出1 |
| 或 | |、or |
有1出1 |
| 异或 | ^、\(\bigoplus\)、xor |
不同出1 |
这一块的内容比较散乱,以海量刷题为首要学习方向,同时需要收集一些常用结论。
常用结论
- 对于给定的 \(X\) 和序列 \([a_1,a_2,\dots,a_n]\) ,有:\({X=(X {\rm and} a_1) {\rm or} (X {\rm and} a_2) {\rm or} \dots {\rm or} (X {\rm and} a_n)}\) 。
原理是 $ {\rm and} $ 意味着取交集,$ {\rm or} $ 意味着取子集。
题单
牛客小白月赛49C - 圣:考察了常用结论;
abc147_d - Xor Sum 4:基础拆位操作;
题意:给定长度为 \(N\) 的序列 \(A\) ,计算 \(\displaystyle \sum_{i=1}^{N-1}\sum_{j=i+1}^{N}(A_i \oplus A_j)\) 。
单纯位运算。拆位,对于每一位而言,只有 \(0\) 和 \(1\) 相互组合才能产生贡献,所以每一位的贡献即为 \(0\) 和 \(1\) 的乘积: \(cnt_0 \cdot cnt_1 \cdot 2^i\) 。
坑:别忘了取模。
signed main() {
int n;
cin >> n;
vector<int> bit(60);
for (int i = 1; i <= n; i++) {
int x;
cin >> x;
bitset<60> val = x;
for (int j = 0; j < 60; j++) {
bit[j] += val[j];
}
}
Z ans;
for (int i = 0; i < 60; i++) {
ans += (Z)bit[i] * (Z)(n - bit[i]) * (Z)(1LL << i);
}
cout << ans << endl;
}
abc117_d - XXOR:基础拆位操作,与上一题几乎一致;
题意:给定长度为 \(N\) 的序列 \(A\) ,在 \([1,K]\) 范围内取一个 \(X\) ,使得 \(\displaystyle \sum_{i=1}^{N}(A_i \oplus X)\) 最大。
单纯位运算。和上一题差不多的思路,略难一点。首先每一位的贡献还是 \(0\) 和 \(1\) 的乘积,从高位到低位遍历,判断 \(X\) 的这一位为 \(0\) 合适还是为 \(1\) 合适(即判断 \(cnt_1\) 是否大于 \(cnt_0\) );若为 \(1\) 合适,判断是否会超过 \(K\) 的限制。
坑:数据比较弱,一开始多加了个排序的贪心,结果就WA了一个点。
signed main() {
int n, k;
cin >> n >> k;
vector<int> bit(40);
for (int i = 1; i <= n; i++) {
int x;
cin >> x;
bitset<40> val = x;
for (int j = 0; j < 40; j++) {
bit[j] += val[j];
}
}
int X = 0, ans = 0;
for (int i = 39; i >= 0; i--) {
if (n - bit[i] > bit[i] && X + (1LL << i) <= k) {
X += (1LL << i);
ans += (n - bit[i]) * (1LL << i);
} else {
ans += bit[i] * (1LL << i);
}
}
cout << ans << endl;
}
arc098_b - Xor Sum 2:考察了异或的常用性质。
题意:给定长度为 \(N\) 的序列 \(A\) ,求解区间 \([l,r]\) 的数量,使得 \(a_l,a_{l+1},\dots a_{r-1},a_r\) 的异或和等于和。
位运算+尺取+暴力,也有双指针、二分解。由于位运算满足 \(x\oplus x\oplus x=0\) ,符合尺取性质,所以直接暴力即可。
如果用二分或者双指针解,可能需要用到:如果两个元素的某一位均为 \(1\) ,那么其异或和一定小于和,所以我们需要寻找这样的一个区间,对于每一位均满足这一位为 \(1\) 的元素数量不超过一个。
signed main() {
int n;
cin >> n;
vector<int> a(n + 1);
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
int ans = 0, val = 0;
for (int l = 1, r = 0; l <= n; l++) {
while (r + 1 <= n && (val ^ a[r + 1]) == val + a[r + 1]) {
r++;
val ^= a[r];
}
ans += r - l + 1;
val ^= a[l];
}
cout << ans << endl;
}
1879D(\(\tt *1700\);位运算、拆位技巧)
1777D(\(\tt *1900\);数学、树-搜索、位运算、概率)
相当不错的题目,强思维轻代码。首先很显然一点是这棵树中为 \(1\) 的节点数量会越来越少,其实推广下可以发现第 \(i\) 轮根节点的值就是深度为 \(i\) 的节点的初始值的异或和,整棵树的操作过程可以抽象的看成海浪上岸的过程。
随后理性认知,对于 \(2^n\) 种情况,其实就是等概率全随机的情况,每个位置均有 \(2^{n-1}\) 种情况为 \(1\),该值一定会被计入总答案;随后,对于每一个非叶子节点 \(i\),其子节点又会至多对其进行 \(h_i\) 次更新操作(这里的 \(h_i\) 为 \(i\) 到其子树中最深的叶子节点的距离),我们尝试计算这一部分的贡献——由于等概率全随机,这些点就会有 \((h_i-1)\cdot 2^{n-1}\) 种情况为 \(1\)。
综合上述情况,总结答案即为 \(2^{n-1}\cdot \sum h_i\),所以只需要跑一遍树上搜索即可得到答案。
16E(\(\tt *1900\);概率、状压dp、位运算)
104468J:位运算、暴力、数学
__builtin_clz 模板。
1634B - Fortune Telling(\(\tt *1400\);位运算、数学)
典题。由于 \(x\) 和 \(x+3\) 的初始奇偶性不相同,而按照结论,操作后奇偶性依旧不变,故只需要判断操作后 \(x\) 和 \(y\) 的奇偶性即可。
一个正整数 \(x\) 异或、加上另一个正整数 \(y\) 后奇偶性不发生变化:\(a+b\equiv a\oplus b(\bmod2)\) 。
1095C - Powers Of Two(\(\tt *1400\);位运算、数学)
典题不会,原地坠毁!
结论1:\(k\) 合法当且仅当
__builtin_popcountll(n) <= k && k <= n,显然。结论2:\(2^{k+1}=2\cdot2^{k}\) ,所以我们可以将二进制位看作是数组,然后从高位向低位推,一个高位等于两个低位,直到数组之和恰好等于 \(k\) ,随后依次输出即可。举例说明,\(\{ 1,0,0,1\} \rightarrow \{ 0,2,0,1\} \rightarrow \{ 0,1,2,1\}\) ,即答案为 \(0\) 个 \(2^3\) 、\(1\) 个 \(2^2\) 、……。
代码:
signed main() { int n, k; cin >> n >> k; int cnt = __builtin_popcountll(n); if (k < cnt || n < k) { cout << "NO\n"; return 0; } cout << "YES\n"; vector<int> num; while (n) { num.push_back(n % 2); n /= 2; } for (int i = num.size() - 1; i > 0; i--) { int p = min(k - cnt, num[i]); num[i] -= p; num[i - 1] += 2 * p; cnt += p; } for (int i = 0; i < num.size(); i++) { for (int j = 1; j <= num[i]; j++) { cout << (1LL << i) << " "; } } }
1829H - Don't Blame Me \(^{*1700\text{;dp、位运算}}\)
1368D - AND, OR and square sum
个人感觉这题有两个解题思路。
其一是,我们需要发现题目中给定的操作只会将 \(x\) 二进制模式下的全部 \(1\) 移动到 \(y\) 的对应位置上。这个规律可以打表得到,如下图:
bool Solve() {
int A, B;
cin >> A >> B;
bitset<10> x = A;
bitset<10> y = B;
_(x);
_(y);
_(x|y);
_(x&y);
return 0;
}
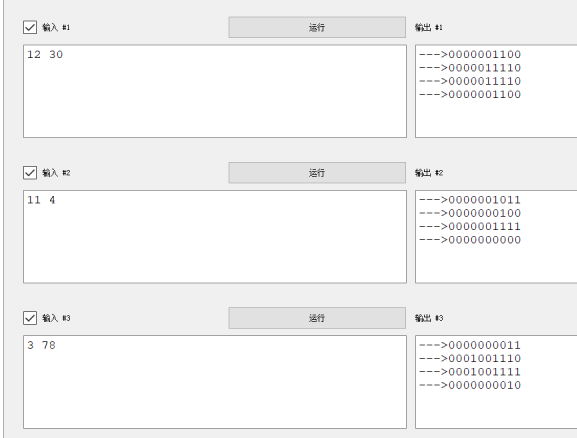
这有什么用呢?这说明 \(1\) 是可以无损移动的,那么我们尽可能让 \(a_i\) 的大小差距拉开(大的尽可能大、小的尽可能小),就可以使得所求最大。
第二个做法更不容易想到,如下。首先,位运算有个公式:\(x+y=x|y+x\&y\) 。根据这个公式我们可以知道,题目中定义的操作不会影响 \(\displaystyle\sum_{i=1}^n a_i\) 的值。
那么,问题在于 \(\displaystyle\sum_{i=1}^n a_i\) 和我们要求解的式子有什么关系呢……显然,根据高中数学,我们有公式 \(\displaystyle\sum_{i=1}^n a_i^2 =(\sum_{i=1}^n a_i)^2-2\cdot \sum_{i=1}^{n}\sum_{j=i+1}^{n}a_ia_j\) ,此时已知操作不会改变 \(\displaystyle(\sum_{i=1}^n a_i)^2\) 的值,所以要使得 \(\displaystyle\sum_{i=1}^n a_i^2\) 最大,即要让 \(\displaystyle\sum_{i=1}^{n}\sum_{j=i+1}^{n}a_ia_j\) 最小。
现在的问题变成了怎样分配 \(a_i\) ,使得 \(\displaystyle\sum_{i=1}^{n}\sum_{j=i+1}^{n}a_ia_j\) 最小,我们发现,当 \(0\) 的数量最多时,乘积也有最多的 \(0\) 。所以,我们需要让 \(a_i\) 的大小差距拉开。
1721D - Maximum AND
超级好题
1554C - Mikasa \(^{*1800\text{;位运算}}\)
巧妙的使用了异或“半加”的性质解题。
1365E - Maximum Subsequence Value
有意思的位运算题。
484A - Bits(*1700 + 构造 + 位运算)
非常考验位运算思维的一题,不难,分数比较虚高。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号