学习笔记——刷题小记(2)
前言
年刷千题时刻图置顶。我超级刷的完!
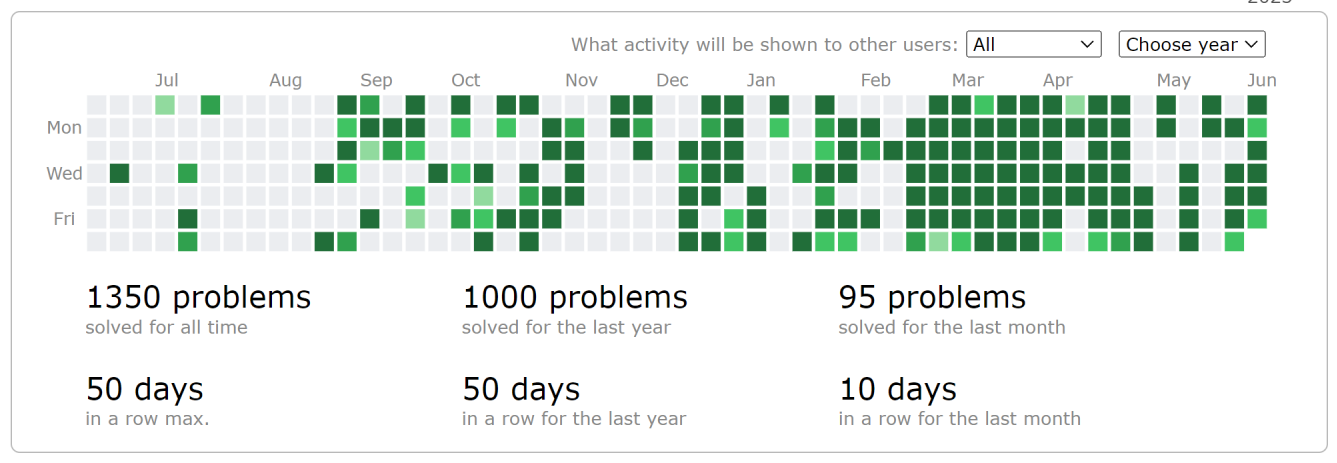
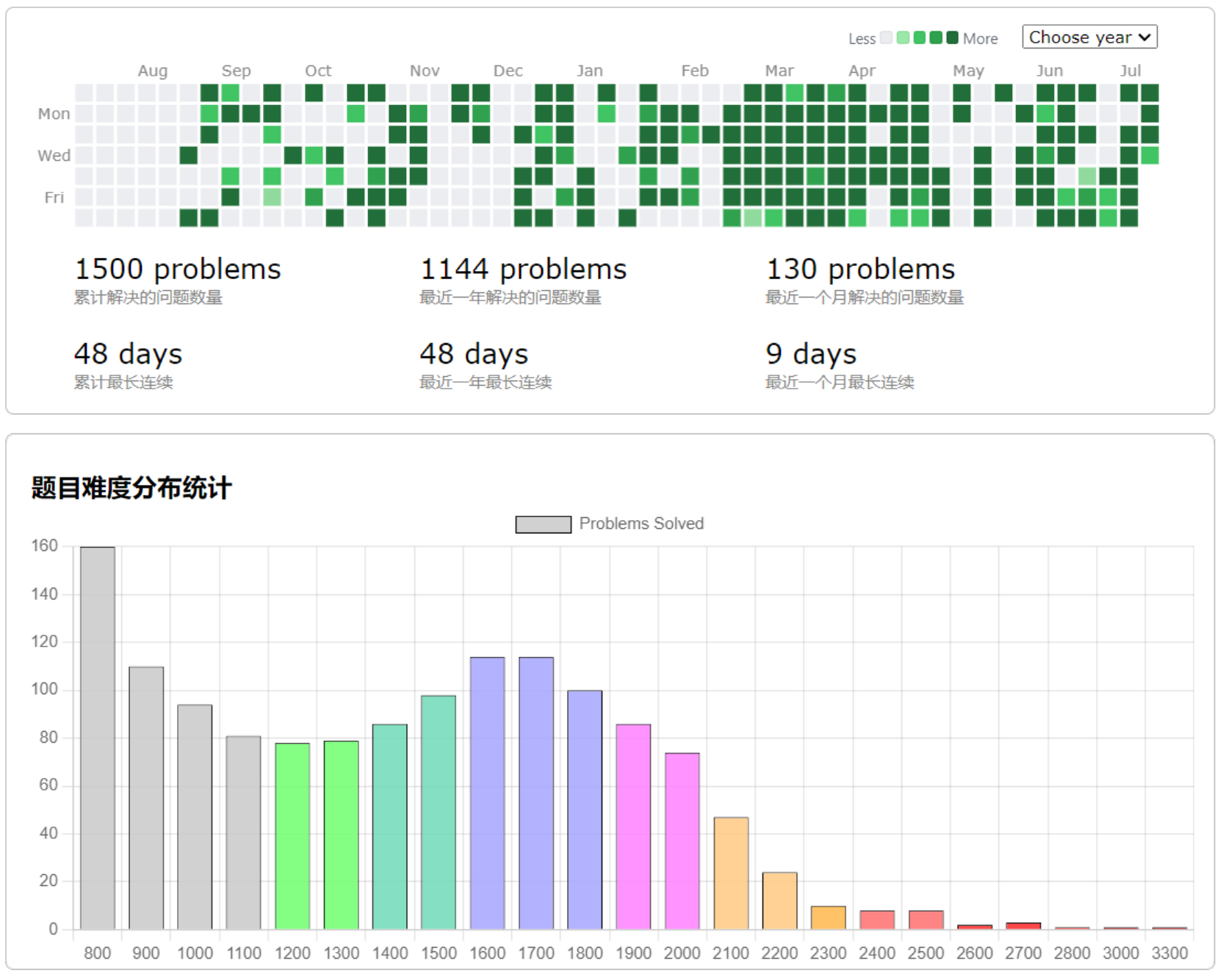
累计1K5以及优美难度曲线。
备注
\(\color{#d0af4c}{\text{#d0af4c}}\) :模板题。
\(\color{#5c9291}{\text{#5c9291}}\) :好题。
\(\color{#9d5b8b}{\text{#9d5b8b}}\) :需要重构。
\(\color{#df0030}{\text{#df0030}}\) :Wrong Answer。
上色格式参考:
<font color = '#5c9291'> 这里填写标题 </font>
题目标签格式参考
### 题目编号 - 题目名称($\tt *2000$;标签1、标签2)
比赛部分的刷题小记参见 Vjudge题单。
2023.11.03
13C(\(\tt *2200\);数据结构-优先队列、贪心)
同时也是凸函数优化 dp 板题。
713C(\(\tt *2300\);数据结构-优先队列、贪心)
双倍经验。
2023.10.30
85D(\(\tt *2300\);数据结构-权值线段树、暴力)
权值/值域线段树简单应用(200 ms);也可以使用 vector 暴力模拟(\(\mathcal O(5E8)\), 900ms)。
2023.10.29
438D(\(\tt *2300\);数据结构-线段树)
Segt List #1 | 二刷,单点赋值+区间取模+区间询问。
2023.10.28
1043F(\(\tt *2500\);数论-筛+容斥+反演、动态规划、暴力、复杂度欺骗)
复杂度欺骗是第一点,即答案不超过 \(7\) ;
暴力枚举答案 \(x\) 、暴力枚举选出数字的 \(\gcd=y\) ,随后设法 \(\mathcal O(1)\) 统计从 \(n\) 个数字中选取 \(x\) 个数且 \(\gcd\) 为 \(y\) 的方案数:
- 想到可以利用筛法筛出某个数的全部倍数,上述方案的选取一定是从这些倍数中选的,具体的说假设底数为 \(y\) ,找到 \(y\) 的全部倍数,假设数量为 \({\tt Count}_y\) ,那么 \(\dbinom{{\tt Count}_y}{x}\) 即为上方想要求得方案数的一部分,注意是一部分!因为 \(\gcd\) 为 \(y\) 的倍数的方案数也被包括进去了;
- 随后发现可以逆着枚举 \(y\) ,这样可以枚举出 \(y\) 的全部倍数随后减去这些倍数的方案数,即为容斥。
\({\tt Count}_y\) 可以用筛法预处理,最终整个算法的复杂度即为 \(N\log N\) 。
需要注意的是在求方案数的时候会超过 long long 的范围,注意到有人采用取模的方式(类哈希法)规避,但是我认为这是不严谨的,哪怕撞哈希的几率很小,但还是不太能接受,于是使用了 __int128 精确计算。
1036F(\(\tt *2400\);数论-筛、暴力)
没别的,只是因为这个题存在数据会使得 sqrt 精度丢失,需要手写开方函数(使用 sqrtl 也能过):
i64 mysqrt(i64 n) {
i64 ans = sqrt(n);
while ((ans + 1) * (ans + 1) <= n) ans++;
while (ans * ans > n) ans--;
return ans;
}
2023.10.26
161C(\(\tt *2400\);分治、贪心、复杂度欺骗)
核心思路是,既然中轴线两侧的字符串相等,那就直接做镜像对折到一起,使得当且仅当两个字符串存在重叠部分时才进行答案计算,而一旦存在重叠,则立即停止分治(继续分治答案一定更劣)。分析复杂度可以发现,单次对折有四种折叠方式,如果不进行剪枝,理论最坏复杂度为 \(4^30\) ,但是显然,由于存在重叠部分后立即停止分治这一剪枝,单次分治在 \(\log\) 复杂度内便会停止,实际运行效率会极高。
细节的地点在于如何镜像对折,即边界的 \(+1/-1\) 问题。
2023.10.25
985D(\(\tt *2100\);二分、数学)
题目读懂了就能发现是满足二分性质的(一开始没读懂,想不通为什么二分),随后就需要一些分类讨论+二分思维,刚开始我针对的是最高堆的高度进行的二分的,这就导致算答案非常麻烦,后来发现直接二分堆数即可。需要注意本题细节比较多,二分范围、数值是否超过 int 都需要注意,但是如果不在意这种边界情况,使用 define int lonng long 和较为宽松的二分范围应该可以无伤通过本题。由于是训练题,所以我使用的是精细的运算,这导致我因为边界问题错误了好多次,不过这也提醒我我对于边界的掌控仍然非常不过关。
2023.10.21
45G(\(\tt *2200\);数论-哥德巴赫猜想)
已加入板子。考察哥德巴赫猜想,记全部数字之和为 \(S\) ,分类讨论如下:
- 为 \(S\) 质数时,只需要分入同一组;
- 当 \(S\) 为偶数时,由猜想可知一定能分成两个质数,可以证明其中较小的那个一定小于 \(N\) ,暴力枚举分组;
- 当 \(S-2\) 为质数时,特殊判断出答案;
- 其余情况一定能被分成三组,其中 \(3\) 单独成组,\(S-3\) 后成为偶数,重复讨论二的过程即可。
45D(\(\tt *1900\);排序、贪心)
经典的排序贪心题,需要考虑谁作为第一下标更贪心,较难。
45C(\(\tt *1900\);数据结构-STL、数据结构-链表)
纯血数据结构题。需要维护一个类似链表的结构+一个堆。
2023.10.17
6E(\(\tt *1900\);数据结构-STL)
multiset 教学题,类似于单调队列的结构。由于需要获取容器首尾元素,直接使用 begin() 和 rbegin() 函数即可(此前我都是 begin() 和 prev(end()))。
2023.10.16
15C(\(\tt *2000\);博弈论-Nim、数论)
每辆车都是一个独立的 Nim 游戏,整个系统构成 Multi-Nim 局面,暴力计算即可。问题在于如何暴力计算连续数的异或和,三年前存的模板在此时派上了用处;如果没有模板,暴力打表找规律可以得到相似结果。
以 \(\mathcal O(1)\) 复杂度计算 \(0\oplus1\oplus\dots\oplus n\) 。
unsigned xor_n(unsigned n) { unsigned t = n & 3; if (t & 1) return t / 2u ^ 1; return t / 2u ^ n; }
除此之外,暴力打表可以得到相似的东西:
i64 xor_n(i64 n) {
if (n % 4 == 1) return 1;
else if (n % 4 == 2) return n + 1;
else if (n % 4 == 3) return 0;
else return n;
}
2023.10.15
7C(\(\tt *1800\);数论-扩展欧几里得)
exgcd 模板题。
9D(\(\tt *1900\);树-树形dp、动态规划-树形dp)
比较新奇的dp题,可以常做提思维。
2023.10.13
1003F(\(\tt *2200\);字符串-哈希、字符串-KMP、暴力)
string - hashing List #5 | 比较难受的一题,原先的字符串板子传递变量的时间过慢导致一直超时,但是难度并不是很高。
首先观察到单个字符串长度极长但是数量很少,于是想到使用字符串哈希将总长度缩小,属于比较典的思路,使用 map 即可轻松做到这一点;随后暴力枚举全部匹配情况后依次统计次数即可,借助 KMP 可以在 \(\mathcal O(N^3)\) 完成。注意,如果使用 find 函数规避 KMP ,那么理论最坏复杂度会上升到 \(\mathcal O(N^4)\),我一开始是由于读错了题,以为至多可替换两段内容,于是没有使用 KMP,导致超时。
另外还有一点需要注意的是,上述的复杂度需要简单修改 KMP 函数使之能够对哈希后的数组进行匹配,如果使用 to_string 函数对哈希后的数组再处理回字符串后运行 KMP(没错,我一开始真的这样写了),复杂度会上升到最坏 \(\mathcal O(N^2 \cdot \sum_{i=1}^{200})\),这样依旧会超时。
另外,注意到我们是暴力枚举后进行匹配,未被枚举到的部分其实不需要进行匹配,所以本题有一个修改 KMP 匹配范围进行优化的方法,使得单次只匹配使用到的那部分内容,可以简单学习。根据这一优化方式,抽象了一个“统计原串中某个子串重复出现的次数”的板子。
7D(\(\tt *2200\);字符串-哈希)
string - hashing List #4 | 哈希判回文,较模板。单哈希即可通过,双哈希有超时风险。观察到有较高效的做法 See 。
25E(\(\tt *2200\);暴力、字符串-哈希、字符串-KMP)
string - hashing List #3 | 暴力枚举后运行两个字符串算法,较模板。写这题的过程中综合了之前做过的字符串哈希的题目形成了一个较为系统的哈希相关封装。
2023.10.12
25C(\(\tt *1900\);图论-最短路、动态规划-Floyd)
DP List #7 | Floyd简单变形,比较好做但是题目范围有误,导致爆 long long 了……早期cf场子规范性真的不太行。
27D(\(\tt *2200\);图论-2sat)
2-sat模板,一眼看出就是P3209的弱化版,现已加入代码模板。
2023.10.11
19B(\(\tt *1900\);动态规划-01背包)
01背包的简单变形,难点在于体积和价格维度需要进行交换,同时背包容量的设计也需要格外小心。
另外本题数据较弱,我hack掉了21年AC这题时的代码 See 。
21D(\(\tt *2400\);图论-多源汇最短路、图论-欧拉回路、图论-一般图最大权匹配)
显然我们需要输出一条最小权欧拉回路,由于一条边可以重复走,我们需要人为的增加一些边到图中使得新图存在欧拉回路、且权最小。首要解决的问题是如何构建欧拉回路,显然我们有性质“入度均为偶数”,故拿出全部的奇数点两两连边即可。
代码的差异化在于连边的过程,显然,我们可以用多源汇最短路求解出固定两点间最短的连边方式,但是如何选择出这样固定的两点,我们有两个解法,其一是暴力+状压dp,复杂度 \(\mathcal O(2^N)\) 足以通过;其二是使用最大权匹配算法,二分图的 KM 算法以及一般图的带花树算法均可以做到 \(\mathcal O(N^3)\) 的复杂度,但是前者需要建立一张二分图,比较难,于是我最终选用了后者。
最后,将新连的边加入图中后运行欧拉回路算法计算总权值即可。
2023.10.10
HDU-4055(动态规划)
DP List #6 | 群友给的。高难,递增与递减的处理思路不同,但是最终可以转化为较为相似的代码;随后需要前缀和优化。
507D(\(\tt *2200\);动态规划-数位dp)
DP List #5 | 普通数位dp,但是需要动态取模,于是修改了板子。
383D(\(\tt *2300\);动态规划)
DP List #4 | 普通动规题,但是由于过程中会有负数,故需要坐标偏移。总体不难。
372B(\(\tt *1900\);动态规划-最小矩形问题)
DP List #3 | 好题,新奇思路。前缀和套二维前缀和套二维前缀和,最后那个不套复杂度应该也能过。
2023.10.09
33C(\(\tt *1800\);贪心、暴力)
近些日子来遇到的最离谱的题,可能也是刷了这么多题一来印象最深的一道。如果要用正向贪心来解,代码极长极难;但是逆向贪心基于暴力,仅用一个循环即可解决问题,代码非常简洁、且没有思维量。
4D(\(\tt *1700\);动态规划-LIS问题)
DP List #2 | 二维LIS带输出方案。\(\mathcal O(N^2)\) 的动规做法比较好写,\(\mathcal O(N\log N)\) 的二分较难,不过好在两者都能通过。后者已收入板子。
106C(\(\tt *1700\);动态规划)
DP List #1 | 普通动规题。
2023.10.08
1519D(\(\tt *1600\);暴力、双指针)
和马拉车的原理极其相似,即从枚举整个子串变为枚举中心后外扩,过程中维护外扩所产生的贡献即可。这样做使得复杂度从 \(\mathcal O(N^3)\) 优化至 \(\mathcal O(N^2)\),属于比较经典的做法。
962E(\(\tt *2200\);贪心、构造)
比较极致的贪心,能够想到贪心的构造方式首先就是难点,可以参考这一篇博客,讲的比较不错,随后,模拟实现这一贪心过程也比较困难。
2023.10.06
1879E(\(\tt *2400\);交互、构造、树-搜索)
不是很懂。
1879D(\(\tt *1700\);位运算、拆位技巧)
位运算好题。
1879C(\(\tt *1300\);组合数学)
组合数学好题。
2023.10.05
995A(\(\tt *2100\);构造、大模拟)
XX大模拟。
2023.09.28
700C(\(\tt *2600\);图论-缩点、网络流-最小割)
洛谷博客。
807C(\(\tt *1700\);二分答案、数学)
比较高难、新颖的二分,要想到二分比较困难。
2023.09.26
351B(\(\tt *1900\);概率)
弱智题目,难度都在读题上。没什么可说的,随便推下就出来了。
1777C(\(\tt *1700\);数学、双指针、复杂度欺骗)
调和级数复杂度计算。预处理完全部数字的因数后进行双指针处理。
1777D(\(\tt *1900\);数学、树-搜索、位运算、概率)
相当不错的题目,强思维轻代码。首先很显然一点是这棵树中为 \(1\) 的节点数量会越来越少,其实推广下可以发现第 \(i\) 轮根节点的值就是深度为 \(i\) 的节点的初始值的异或和,整棵树的操作过程可以抽象的看成海浪上岸的过程。
随后理性认知,对于 \(2^n\) 种情况,其实就是等概率全随机的情况,每个位置均有 \(2^{n-1}\) 种情况为 \(1\),该值一定会被计入总答案;随后,对于每一个非叶子节点 \(i\),其子节点又会至多对其进行 \(h_i\) 次更新操作(这里的 \(h_i\) 为 \(i\) 到其子树中最深的叶子节点的距离),我们尝试计算这一部分的贡献——由于等概率全随机,这些点就会有 \((h_i-1)\cdot 2^{n-1}\) 种情况为 \(1\)。
综合上述情况,总结答案即为 \(2^{n-1}\cdot \sum h_i\),所以只需要跑一遍树上搜索即可得到答案。
16E(\(\tt *1900\);概率、状压dp、位运算)
位运算好题。
518D(\(\tt *1700\);期望dp)
标准的概率dp,二维。
2023.09.21
104369D:前缀和、排序
贪心大失败!好题,改正了我遇题不决用贪心的思路。前缀和解决这个题目又靠谱又快,感觉出过很多次类似的题目了,记录一下。
104466B:几何、暴力、组合数
比较巧妙的暴力题,任选四个点作直线后在剩余点中任选三个点作直线,如此可以枚举出全部状态,最终判定剩下的点是否在同一直线上即可。
复杂度 \(\mathcal O\left(N\cdot\binom{4}{2}\binom{3}{2}\binom{2}{2}\right)\)。
104466C:期望、图论-最短路
难得一遇的好题,出题人在难度方面的把控令人赞叹。期望部分概念稍难于模板题(考察期望公式 \(E_{aX+bY}=aE_X+bE_y\)),删去了 dp 推导但是加上了一个分数运算;图论部分也稍难于模板题。
2023.09.20
104468M:组合数学
即求解有多少个排列,使得 \(p_i<p_{i+1}\) 且 \(i\) 不在集合中。
104468H:二分查找、数据结构-STL
比较简单的二分查找题,仅在模板上进行了一点点点点的修改,另外套了一个数据结构的外壳,属于比较好的铜牌题。
104468J:位运算、暴力、数学
__builtin_clz 模板。
2023.09.18
104363G:几何、排序、贪心、数论
多边形重心+叉乘本质/性质。
2023.09.14
P5782(2Sat)
建图比较特殊。对于给出的每一对相互厌恶的代表 \((x,y)\),假设他们所在党派的另一人是 \((x',y')\),那么我们建边为 \((x,y')\) 和 \((x', y)\)。由于编号给定,要根据原封装中的 add 函数进行二次修改过于繁琐,直接另写一个普通的 add 函数即可。
P3209(2Sat、几何、图论)
增加了几何背景,发现对于某一条边,其只能在给定回路的内部/外部穿过,满足性质,随后我们只需要用几何+图论知识判断那些线段可能会相交,随后建图即可。相较于模板变化并不大。
P3007(2Sat)
很难,相较于模板多了一个不确定的输出,需要单独进行判定。
P4171(2Sat)
模板,几乎不用修改。
P4782(2Sat)
补了一道模板题,测试了下板子。
776D(\(\tt *2000\);数据结构-并查集、2Sat)
两个解法,都基本属于模板题。
方法一:扩展域并查集
方法二:2Sat。
1657D(\(\tt *2000\);二分搜索、复杂度欺骗、数学、排序、贪心)
移项后容易发现式子需要满足 \(d_i\cdot h_i >D_j \cdot H_j\),于是按照每个人的价格贪心排序,相同价格取最 \(d_i\cdot h_i\) 最大的那个士兵,随后暴力计算全部的购买情况。对于每个询问,使用二分查找即可找到最优解。
这里暴力计算的复杂度是经典的调和级数,故不会超时。
2023.09.13
1200E(\(\tt *2000\);字符串、暴力、哈希)
string - hashing List #2 | 字符串后缀哈希,感觉是很典的题目。
1363E(\(\tt *2000\);图论-搜索、贪心)
常规贪心。
1359E(\(\tt *2000\);组合数)
虚高组合数题。
2023.09.09
P3370(字符串哈希)
补了一道模板题,测试了下板子。
514C(\(\tt *2000\);字符串、数据结构-字典树、搜索、暴力、哈希)
注意到串仅由三个字母构成。方法一是很显然的,建立字典树后在树上进行搜索匹配串:针对匹配串的每一位,暴力枚举其三种不同构成,最终以 \(\mathcal 3\cdot \sum N\) 的复杂度完成搜索。针对该方案有如下优化:\(\tt ^1\) 不使用 auto 进行搜索,而是直接用单独的函数进行,前者在实现上花费的时间更长一些;数组不留余量,使用 \(\tt 0-idx\) 法,这一优化可以提速近乎一倍,推测原因是减少了数组跳转的次数,应当引起注意。
string - hashing List #1 | 下面介绍字符串方面的方法:字符串哈希。本题使用单哈希需要将模数固定在 \(10^{10}\) 量级以上,不然会撞;如果是双哈希则没有特别的限制。属于字符串哈希的模板题,但是需要手写一个 \(\mathcal O(1)\) 进行某一位修改的函数(本质上是与方法一暴力修改一样的思路),比较考验对哈希过程原理的理解。
1288D(\(\tt *2000\);二分搜索、状态压缩、暴力)
突破口在于 \(m\) 的范围,应当要一眼意识到这是状压的征兆。随后用到852D相似的技巧,“二分算出上限后连接全部不超过上限的边”,在本题中,即将超过上限的位置为 \(1\),由于状压,最终的方案数不超过 \(2^8\) 种,故我们只需要暴力枚举检查是否成立即可。
注意由于题目要求取出的是全部位中的最大值,故当且仅当暴力枚举的两个数的 \(\tt or\) 为 \(\tt 11111111\) 时才被纳入答案。
2023.09.08
1472F(\(\tt *2100\);数据结构-STL、暴力枚举、模拟)
大模拟题。
269C(\(\tt *2100\);构造、图论-拓扑排序)
比较简单的构造。
852D(\(\tt *2100\);图论-最短路、二分搜索、网络流-二分图匹配)
虽然涉及的算法多,但是都比较模板。二分算出上限后连接全部不超过上限的边、随后跑网络流,属于比较典的东西了。
1583E(\(\tt *2200\);图论-生成树、构造算法)
和1470D的区别在于这道题需要先随便找出一棵生成树。
1034B(\(\tt *2200\);暴力)
纯找规律题……
723E(\(\tt *2200\);图论-欧拉回路)
欧拉回路模板。
P7771(图论-欧拉路径)
有向图欧拉路径,去刷的模板题。
P1341(图论-欧拉路径、字符串)
无向图欧拉路径,去刷的模板题。
510E(\(\tt *2300\);网络流-最大流、网络流-残留网络搜索)
在残留网络上搜索哪些边被使用过的模板题。由于建图时是二分图、奇数连源,故搜索时相对应的,奇数时使用正向边,无流量说明被使用;偶数时使用反向边,有流量说明被使用。
2023.09.07
1486E(\(\tt *2200\);图论-最短路、暴力、图论技巧-拆点、图论技巧-新建点)
很难。关注到我们没办法建立原图,但是 \(w\) 的范围很小,考虑利用其建图。
先讲第一个暴力建边的思路,需要卡常数才能通过。对于 \((x,y)\),新建一个 \(x\) 的辅助点 \(t\),然后将 \((x,t)\) 连接,边权为 \(0\);再新建一个 \(y\) 的辅助点 \(s\),然后暴力枚举 \((s,y)\) 之间可能出现的全部边权,一共 \(50\) 条边,依次建边。由于是双向边,反过来再进行一次上面的操作,总边数 \(50M+M\),对这张图跑最短路算法,总复杂度 \(\mathcal O\big((50M+M)\log(50N+N)\big) \approx 3E8\) 。
随后我们不将这个图建出来的思路,这一方法不需要用到拆点和新建点的技巧,而是利用djikstra本质进行修改。对于第一层的点,我们将其答案储存到 dis[x1][0] 中去,随后传递标记 \(w1\) 到下一层,在 dis[x2][w1] 中更新答案,随后传递标记 \(0\) 到再下一层,重复上方的操作即可。总复杂度 \(\mathcal O(M\log N)\)
1470D(\(\tt *2200\);图论-搜索、构造、数据结构-并查集)
虚高构造题。判完图是否连通后搜索染色即可,当一个点周围全部点均未被染色时将这个点染色,感觉这个思路很常见。
2023.09.01
1401E(\(\tt *2400\);数据结构-树状数组、模拟、排序)
其实与1194E很像,都是类似于扫描线的思路,但是这题貌似更简单;与AtCoder past202004_n的离线+树状数组的思路也很近似,离线排序、固定一个维度后将二维问题转化为区间问题,用树状数组解决。
2023.08.29
1194E(\(\tt *2200\);数据结构-树状数组、贪心、坐标偏移与压缩、排序)
创新题。暴力枚举横线、利用了树状数组+贪心进行竖线的维护。
429D(\(\tt *2200\);数据结构-set)
平面最近点对模板。
1059D(\(\tt *2200\);三分)
比较版的三分求极值,但是方程的推导需要花点时间,可以 参考 。
406D(\(\tt *2200\);几何、树-LCA)
很好的好题,考察了两个东西,其一是叉姬的定义公式 \(a\times b=|a||b|\sin \theta\),其二是求解LCA。后者只要学过LCA就是是一眼的事情,我们主要来分析下前者。
要想到叉姬并不容易,主要是这个题目描述的很模糊,我是看到加粗的那句“爬到能到达的最右边的山顶”才意识到的,如果山头 \(i\) 和 \(k\) 中间有个 \(j\) 使得 \(i\) 不能直接到达 \(k\) ,那么一定有 \(\angle ijk \ge 180 ^{\circ}\)(这里的角是开口朝下的那个角),而这一东西可以用叉姬顺手算出来。至此,我们可以建树后跑LCA。
2023.08.28
689D(\(\tt *2000\);二分搜索、数据结构-ST表)
静态区间查询最大最小值,用了ST表,顺手更新了下板子。
1454F(\(\tt *2100\);二分搜索、数据结构-ST表)
上面那题的孪生,但是这题的二分实现更加困难一些,是练二分的好题。
703C(\(\tt *2100\);思维、模拟)
创新题,思维题,代码很短。虽然题干看起来很可怕,其实化简后就是基于“人要等车”和“人不需要等车”这两个模拟。
P1972(\(\tt *Blue\);贪心、数据结构-树状数组)
模板:区间不同数字的数量(树状数组+离线维护),\(\mathcal O(N\log N)\) 。(备注:莫队也可解,复杂度更高)
核心在于使用 pre 数组滚动维护每一个数字出现的最后位置,配以树状数组统计数量。由于滚动维护具有后效性,所以需要离线操作,从前往后更新。
signed main() {
int n;
cin >> n;
vector<int> in(n + 1);
for (int i = 1; i <= n; i++) {
cin >> in[i];
}
int q;
cin >> q;
vector<array<int, 3>> query;
for (int i = 0; i < q; i++) {
int l, r;
cin >> l >> r;
query.push_back({r, l, i});
}
sort(query.begin(), query.end());
vector<pair<int, int>> ans;
map<int, int> pre;
int st = 1;
BIT bit(n);
for (auto [r, l, id] : query) {
for (int i = st; i <= r; i++, st++) {
if (pre.count(in[i])) { // 消除此前操作的影响
bit.add(pre[in[i]], -1);
}
bit.add(i, 1);
pre[in[i]] = i; // 更新操作
}
ans.push_back({id, bit.ask(r) - bit.ask(l - 1)});
}
sort(ans.begin(), ans.end());
for (auto [id, w] : ans) {
cout << w << endl;
}
}
703D(\(\tt *2100\);贪心、数据结构-树状数组)
上面那题的孪生,但是需要进行一些转化。借用洛谷题解区的描述,“出现偶数次的数的异或和” \(\iff\) “区间异或和 \(\oplus\) 出现奇数次的数的异或和” \(\iff\) “区间异或和 \(\oplus\) 区间内不同数的异或和”。
剩余套路与上面那题一致,只需要修改下树状数组即可。当然,没有铺垫的话这题是一眼莫队,但是赛后 hack 的数据基本卡死了莫队,一般莫队使用的数据范围都在 \(10^5\) 量级。树状数组做法时间瓶颈在于 map 数据,用手造哈希或者离散化可以优化到理想区间。
106E(\(\tt *2100\);几何、三分)
虽然这个题目我不喜欢,但是很有教育意义,所以也算作好题。题目的思路是很好想,即分别对三个坐标轴进行三分计算,实际实现遇到了以下问题:三分模板有误且效率过低、精度存在较大问题、long double 被卡超时。
最终采取了如下措施解决问题:
- 修改了三分模板,现在变为限制查询次数的版本,且针对查询的进行设置了层级式的查询次数,保证精度的同时避免超时;
- 修改了一些函数:不再使用手写的比较函数
sign(刚开始由于EPS忘记修改了导致精度一直不对,后来想要修改EPS但是无从下手,怕超时),而是直接使用符号判断;距离函数替换成了无根号的版本以避免精度丢失; - 将
long double修改为double。
2023.08.25
abc223_e(\(\tt *1671\);暴力、模拟、几何、分治)
非常非常创新的题目,好题。这样的题目应当如何模拟呢,我们巧妙的利用了 swap 函数进行不重不漏的讨论,这样做的好处是在单次模拟的时候我们不需要在进行诸如长宽的讨论、横放还是竖放的讨论。
576C(\(\tt *2100\);暴力、几何、数据结构、排序)
创新题,本质上考察的是莫队的实现思路(然而我写这题发现我莫队板子烂了,于是喜提优化后的新板子)。
1299C(\(\tt *2100\);数据结构)
类似于单调栈的实现。
abc191_d(\(\tt *1953\);几何、编程技巧、二分答案)
卡精度题,被恶心到了。我采用的是转化为整数后进行二分,代码较长但是能证明误差与正确性,此外我还看到有用玄学卡精度方式过题的人 链接 ,虽然代码很短但是我没办法证明其正确性(例如将 1E-14 改为 1E-15 就无法通过样例;对 \(x,y\) 同样进行偏移操作也无法通过)。
2023.08.24
1819B - The Butcher(\(\tt *1900\);暴力、模拟、数据结构)
大模拟题,跟区域赛喜欢考的模拟题很类似。主要是使用数据结构进行疯狂模拟,我参考了 jiangly 的思路,使用优先队列+打标记的方式规避了常规做法的查找删除操作,代码较短。
1063C - Dwarves, Hats and Extrasensory Abilities(\(\tt *1900\);二分查找、暴力、几何)
比较创新的二分题目,需要注意的是输出的直线不能穿过询问的点,那么我们此前常用的二分模板就会出现问题,即遇到 l + 1 == r 的情况,难以构造出合适的直线,于是我们这里不进行 +1 操作,取左边界点下面的点 (l, 0) 和右边界点上面的点 (r, 2),两个点连成的直线就是分界线。
848B - Rooter's Song(\(\tt *1900\);模拟、排序、几何、构造、暴力)
很 阴间 创新的模拟题,首先要找规律确定其可以被模拟,随后大力模拟。
由于我排序是单独的一个循环,且没有加 & ,导致排序了但是没保存覆盖,浪费了二十分钟debug……
814D - An overnight dance in discotheque(\(\tt *2000\);几何、树形结构、搜索)
很创新的题目,将圆的覆盖转换为树上问题进行处理。
2023.07.16
1830B - The BOSS Can Count Pairs(\(\tt *2000\);数学、暴力)
由一条件可知满足条件的 \(\min \{ a_i, a_j \} \le \sqrt {2\cdot n}\) ,故暴力枚举 \(\min \{ a_i, a_j \}\) 。
2023.07.11
1393C - Pinkie Pie Eats Patty-cakes(\(\tt *1700\);构造、贪心、数学)
又被典结论题卡爆惹!
考虑将出现次数最多(假设为 \(Max\) 次)的几个字母(假设有 \(cnt\) 个这样的字母)从原序列中提取出来,组合成 \(Max\) 个小集合(使得每个集合中包含的字母数量均不同)。随后考虑,将这些小集合插入序列。由于在未插入序列之前,序列中剩余元素的数量为 \(n-Max\cdot cnt\) ,由于插入 \(Max\) 个,会形成 \(Max-1\) 个段,那么这些段中长度最小的那个即为 \(\left\lfloor\dfrac{n-Max\cdot cnt}{Max-1}\right\rfloor\) 。
由于求解的是相邻集合之间的距离,故还需要加上集合自身的长度 \(cnt-1\) ,最终答案为 \(\left\lfloor\dfrac{n-Max\cdot cnt}{Max-1}\right\rfloor+cnt-1\) 。
2023.07.10
1498E - Two Houses(\(\tt *2200\);暴力、贪心、图论-性质、排序、交互题)
两个做法,都需要较强的图论能力。更推荐做法一。
做法一:利用竞赛图进行推导
先上结论:
在竞赛图中,入度小(出度大)的点能到达入度大(出度小)的点。
证明如下:
打开证明
我们将竞赛图进行缩点,此时对于任意的两个点 \(i\) 和 \(j\) ,其相对位置只有两种情况:在或者不在同一个强连通分量中。
对于前者,这两个点一定能相互到达;对于后者,假设 \(i\) 所在的SCC能够到达 \(j\) 所在的SCC,由于竞赛图两两点之间一定存在边,所以 \(i\) 与 \(j\) 所在SCC的每一个点都存在一条边,且是从 \(i\) 出发的(否则 \(i\) 和 \(j\) 会在同一个SCC中)——所以 \(i\) 能到达 \(j\) ,且出度一定大于 \(j\) 的出度。
由这个结论我们只需要询问入度大的点能飞到达入度小的点,即可获得两个点之间的连通性,那么,如何满足“度的差值最大”这一条件呢?在询问之前,按照“度的差值”从大到小进行排序即可。至多询问 \(n^2\) 次。
signed main() {
int n;
cin >> n;
vector<int> deg(n + 1);
for (int i = 1; i <= n; i++) {
cin >> deg[i];
}
vector<array<int, 3>> poi;
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
poi.push_back({abs(deg[i] - deg[j]), i, j});
}
}
sort(poi.rbegin(), poi.rend());
for (auto [dif, x, y] : poi) {
if (deg[x] < deg[y]) { // 入度小的点,必定能到达出度小(入度大)的点,这里只需要反过来询问
swap(x, y);
}
cout << "? " << x << " " << y << endl << flush;
string op;
cin >> op;
if (op == "Yes") {
cout << "! " << x << " " << y << endl << flush;
return 0;
}
}
cout << "! " << 0 << " " << 0 << endl << flush;
}
做法二:直接利用竞赛图结论
我们有结论:
在竞赛图中,将所有点按入度从小到大排序,随后依次遍历,若对于某一点 \(i\) 满足前 \(i\) 个点的入度之和恰好等于 \(\left\lfloor \dfrac{n\cdot(n+1)}{2}\right\rfloor\) ,那么对于上一次满足这一条件的点 \(p\) ,\(p+1\) 到 \(i\) 点构成一个新的强连通分量。
举例说明,设满足上方条件的点为 \(p_1,p_2\ (p_1+1<p_2)\) ,那么点 \(1\) 到 \(p_1\) 构成一个强连通分量、点 \(p_1+1\) 到 \(p_2\) 构成一个强连通分量。
signed main() {
int n;
cin >> n;
vector<pair<int, int>> poi(n + 1);
for (int i = 1; i <= n; i++) {
int x;
cin >> x;
poi[i] = {x, i};
}
sort(poi.begin() + 1, poi.end());
int sum = 0, st = 1;
int Max = -1, ans1 = 0, ans2 = 0;
for (int i = 1; i <= n; i++) {
auto [deg, idx] = poi[i];
sum += deg;
if (sum == i * (i - 1) / 2) { // 当 st 到 i 构成一个连通块
if (st != i) {
int val = poi[i].first - poi[st].first;
if (val > Max) {
Max = val;
ans1 = idx;
ans2 = poi[st].second;
}
}
st = i + 1; // 更新 st
}
}
cout << "! " << ans1 << " " << ans2 << endl << flush;
}
260D - Black and White Tree(\(\tt *2100\);构造、树)
比较水。由于保证存在,那么黑色节点权值和必定等于白色节点权值和,拿两个数组分别储存黑白节点,然后每次各取出一个连接即可。
Wait,这好像是个结论,放一下。当一棵树可以被黑白染色时,所有染黑节点的度之和等于所有染白节点的度之和。而度与边权直接关联,所以本题中可以将“度之和”推广为“相邻边的权之和”。
需要注意的是可能存在不成树的情况(样例2),这里有一些方式维护,比如tag里面的 \(\tt DSU\) ,但是这都太麻烦了,我采用的思路是:当某一步,黑白节点恰好相互连结成为一个独立的连通块时,判断黑白数组的大小,哪个数组小就往哪个数组里面塞一个空节点,这样即可以破坏当前连通块的独立性,还可以平衡数组中黑白节点的数量,相当奈斯。
signed main() {
int n;
cin >> n;
queue<pair<int, int>> p[2];
for (int i = 1; i <= n; i++) {
int col, w;
cin >> col >> w;
p[col].push({i, w});
}
for (int i = 1; i < n; i++) {
auto [idx0, w0] = p[0].front();
p[0].pop();
auto [idx1, w1] = p[1].front();
p[1].pop();
cout << idx0 << " " << idx1 << " " << min(w0, w1) << endl;
if (w1 > w0) p[1].push({idx1, w1 - w0});
else if (w1 < w0) p[0].push({idx0, w0 - w1});
else if (p[0].size() < p[1].size()) p[0].push({idx0, 0}); // 奈斯的特判
else p[1].push({idx1, 0}); // 奈斯的特判
}
}
1520F2 - Guess the K-th Zero (Hard version)(\(\tt *2200\);二分、数据结构、交互题)
这题的洛谷题解区写的很糟糕,多数人的思路都有较多的冗余,导致非常混乱。实际上做过Easy Version会发现Hard只是在于寻找一个方法使得每一轮的修改可控(即以线性复杂度储存本次修改之后的值),而本题的修改又非常的经典——即永久改变当前位。于是,树状数组、线段树等可以处理区间问题的数据结构便能够轻松完成这一步。
这里啰嗦两句,关于数据结构里面存放的是什么东西,这个还是挺有技术含量的:对于已经询问过的点,储存当前点之前的 \(1\) 的数量,同时,每次修改后都需要同步更新成修改后的值;对于未询问过的点,储存当前点之前被修改的点的数量,但是这个值是用不到的(为了实现“已经询问过的点同步更新成修改后的值”这一功能,所产生的冗余信息),在被访问到的时候直接清空掉即可,即下方代码中“消除刚刚累加和的影响”这一步骤。
最后我们依旧能在不超过 \(20\) 次询问次数的限制下解决本题。
struct Bit {
int n;
vector<int> a;
Bit(int n) : n(n), a(n + 1) {}
int ask(int x) {
int ans = 0;
for (; x; x -= x & -x) ans += a[x];
return ans;
}
void modify(int x, int k) {
for (; x <= n; x += x & -x) a[x] += k;
}
};
signed main() {
int n, t;
cin >> n >> t;
Fwt fwt(n);
vector<int> vis(n + 1);
while (t--) {
int k;
cin >> k;
int l = 1, r = n;
while (l < r) {
int mid = (l + r) / 2, val = fwt.ask(mid);
if (!vis[mid]) { // 此前未被搜索过
vis[mid] = 1;
cout << "? " << l << " " << mid << endl << flush;
cin >> val;
val += fwt.ask(l - 1); // 这里的加法与F1一致
int pre = fwt.ask(mid);
fwt.modify(mid, -pre); // 消除刚刚累加和的影响
fwt.modify(mid + 1, pre);
fwt.modify(mid, val); // 变相单点修改
fwt.modify(mid + 1, -val);
}
if (k <= mid - val)
r = mid;
else
l = mid + 1;
}
cout << "! " << l << endl << flush;
fwt.modify(l, 1);
}
}
1634B - Fortune Telling(\(\tt *1400\);位运算、数学)
典题。由于 \(x\) 和 \(x+3\) 的初始奇偶性不相同,而按照结论,操作后奇偶性依旧不变,故只需要判断操作后 \(x\) 和 \(y\) 的奇偶性即可。
一个正整数 \(x\) 异或、加上另一个正整数 \(y\) 后奇偶性不发生变化:\(a+b\equiv a\oplus b(\bmod2)\) 。
1463B - Find The Array(\(\tt *1400\);构造)
这个题目的证明很有意思。设奇数位之和 \(S_{odd}\) 偶数位之和 \(S_{even}\) ,这两者一定存在一个数字小于等于 \(\dfrac{S}{2}\) ,假设是 \(S_{odd} \le \dfrac{S}{2}\) ,那么我将奇数位 \(b_i\) 全部置为 \(1\) ,偶数位 \(b_i\) 置为相应的 \(a_i\) 后,偶数位的 \(\sum |a_i - b_i| =0\) ,原式 \(\displaystyle \sum_{i=1}^n |a_i - b_i| \le S_{odd} \le \dfrac{S}{2}\) 满足题意。
2023.07.09
1095C - Powers Of Two(\(\tt *1400\);位运算、数学)
典题不会,原地坠毁!
结论1:\(k\) 合法当且仅当
__builtin_popcountll(n) <= k && k <= n,显然。结论2:\(2^{k+1}=2\cdot2^{k}\) ,所以我们可以将二进制位看作是数组,然后从高位向低位推,一个高位等于两个低位,直到数组之和恰好等于 \(k\) ,随后依次输出即可。举例说明,\(\{ 1,0,0,1\} \rightarrow \{ 0,2,0,1\} \rightarrow \{ 0,1,2,1\}\) ,即答案为 \(0\) 个 \(2^3\) 、\(1\) 个 \(2^2\) 、……。
代码:
signed main() { int n, k; cin >> n >> k; int cnt = __builtin_popcountll(n); if (k < cnt || n < k) { cout << "NO\n"; return 0; } cout << "YES\n"; vector<int> num; while (n) { num.push_back(n % 2); n /= 2; } for (int i = num.size() - 1; i > 0; i--) { int p = min(k - cnt, num[i]); num[i] -= p; num[i - 1] += 2 * p; cnt += p; } for (int i = 0; i < num.size(); i++) { for (int j = 1; j <= num[i]; j++) { cout << (1LL << i) << " "; } } }
2023.07.08
1817D - Toy Machine(\(\tt *2700\);模拟)
纯粹的……给高手磨时间用的题,脑子好就能做出来(T宝和蒋老师赛时都没做出来,确实是怪题)。
1838E - Count Supersequences(\(\tt *2500\);组合数学)
本题需要反向求解。考虑如何计算全部的不包含完整的 \(a\) 作为子序列的情况,这里用到的这个思路应当是典,但是我此前没遇到过:即假设 \(b\) 的子序列最长包含了 \(a\) 的前 \(i\ (0 \le i < n)\) 个数,那么有 \(\dbinom{m}{i}\) 种取法,对于剩下的 \(m-i\) 个位置又有 \(k-1\) 种取值方式(理性分析,这里的 \(-1\) 是去除了取到 \(a_{i+1}\) 的情况,否则会导致假设不成立),故答案即为 \(\displaystyle \sum_{i=0}^{n-1} \dbinom{m}{i} \cdot (k-1)^{m-i}\) 。
这里还有一个问题需要注意,即由于 \(m\) 的取值,我们是没办法预处理出上面这个组合数的,但是 \(\sum n\) 是给定的,所以我们直接递推求解就可以了,至多计算不超过 \(\sum n\) 次。
顺便我们发现,\(a\) 序列具体是什么并不影响最终答案。
763B - Timofey and rectangles(\(\tt *2100\);构造)
四色定理相关,但是用不上。根据题目中“长宽均为奇数”和“矩形不重叠”的限定,容易发现答案与端点的横纵坐标奇偶性相关——考虑某个矩形的其中一个端点 \((x,y)\) 满足 \(x,y\) 均为奇数,那么这个矩形的其余三个端点横纵坐标奇偶性也唯一确定,且四个端点的总组合唯一。
故直接判定即可。
1370E - Binary Subsequence Rotation(\(\tt *2100\);构造、贪心)
究极虚高题,我都一眼看出来的构造。
1360H - Binary Median(\(\tt *2100\);位运算、暴力、数据结构-STL)
典?不确定。
我们可以直接计算出删除操作全部完成之后的中位数是第几个串:mid = ((1LL << m) - n + 1) / 2。这个位置在初始的时候的值为 mid - 1 。
如果删除的值大于 mid - 1 ,不会改变这个值;反之,这个值会向后跳转一个(删除前面的某个元素导致后面的元素整体前移,所以 \(mid\) 位置的串也发生改变,这个很好理解),注意,如果跳转到的这个值已经被删除了,还需要继续向后跳转。
由于至多删除 \(100\) 个,至多跳转 \(100\) 个,故线性递推,可以直接得到答案。
输出时,我使用了自以为很简便的方式:
string ans;
while (mid) {
ans = char(mid % 2 + '0') + ans;
mid /= 2;
}
cout << setw(m) << setfill('0') << ans << endl;
但是Jiangly的位运算大法更神,可以学习一下:
for (int i = m - 1; i >= 0; i--)
cout << (mid >> i & 1);
cout << "\n";
675E - Trains and Statistic(\(\tt *2300\);dp、贪心、数据结构-区间RMQ)
这个dp不难想,我尝试完整的描述思路。由题目 \(a_i\ (i + 1 \le a_i \le n)\) 这一条件可以发现,越靠后面的点跳的次数也就越少,尤其是, \((n-1)\) 号点到达终点需且仅需跳一次,\((n-2)\) 号点到达终点至多需要跳两次,所以,我们可以大胆确定逆推的总体思路。
随后确定状态,这一步骤我倒没有特别大的感触,发现要求解 \(\displaystyle \sum_{i=1}^n\sum_{j=i+1}^n \rho_{i,j}\) ,于是干脆直接枚举 \(i\) ——定义 \(f_i\) 为 \(i\) 之后所有点跳到终点的最短距离之和。
回到刚刚确定逆推方针的步骤上,显然,如果某个点 \(i\) 能够跳一次直接到达终点,那么 \(f_i=n-i\) ;如果不行,那么在 \(i+1\) 到 \(a_i\) 这些选择中,选取哪一个点作为中转点才是最优的呢?
我们之前有推论“越靠后面的点跳的次数也就越少”,所以这里进行贪心:对于 \(k\in [i+1,a_i]\) ,\(a_k\) 最大的点一定是最优的。这是一个区间 \(RMQ\) 问题,随便搞个数据结构处理一下就好。所以,转移方程为 \(f_i=f_k+P-Q\) 。其中,\(P\) 的含义在于,\(i\) 之后每个点到达终点均需要先经过 \(k\) ,每个点贡献 \(1\) ,一共贡献 \(P=n-i\) ;\(Q\) 的含义在于,\(k\) 到 \(a_i\) 之间每个点的贡献均会被计算两次,所以每个点需要减去 \(1\),一共减去 \(Q=a_i-k\) 。
675C - Money Transfers(\(\tt *2100\);贪心、构造)
怀疑构造已经成为了高分值低码量题的代名词了。典?应该是典。一个前缀和解决整个题目。
1254B2 - Send Boxes to Alice (Hard Version) \(^{*2100\text{;数论、贪心}}\)
有三道坎,其一是 \(\displaystyle \sum_{i=1}^n a_i\) 一定能被 \(k\) 整除,所以答案从 \(\sum\) 的因数中找;其二是发现对于质因数和质因数的倍数(假如两者都是 \(\sum\) 的因数),取质因数算出来的答案一定不劣于取质因数的倍数算出来的答案,所以我们只需要考虑 \(\sum\) 的全部质因数,至多 \(20\) 个;其三是在 \(k\) 固定的情况下如何计算转移,考虑下方结论即可。
题意:设当前有一个数字为 \(x\) ,减去、加上最少的数字使得其能被 \(k\) 整除。
结论:最少减去 \(x\bmod k\) 这个很好想;最少加上 \(\left(\left\lceil\dfrac{x}{k}\right\rceil * k\right)\bmod k\) 也比较好想,但是更简便的方法为加上 \(k-x\bmod k\) ,这个式子等价于前面这一坨。
总体来说并不难,分数是虚高的,确切分数在 \(\tt *1900\) 左右。
2023.07.06
107B - Basketball Team \(^{*1600\text{;概率、dp}}\)
概率问题常规正反两解:
解法一:正向dp
我自己是用概率递推正着解的(也可以看作是dp吧),写了一个多小时,感觉自己脑子不太够用……简单来说,\(dp_{i,j}\) 代表前 \(i\) 个人中有 \(j\) 个人与自己同一专业,设 \(x\) 为剩下的与自己专业相同的人数,\(y\) 为剩下的与自己专业不同的人数。随后递推公式为 \(dp_{i,j}=dp_{i-1,j}\times\dfrac{y}{x+y}+dp_{i-1,j-1}\times\dfrac{x}{x+y}\) 。
注意递推式子中第一项和第二项的 \(x,y\) 并不相同,需要分别计算;以及当 \(j=0\) 时需要单独讨论。
signed main() {
int n, m, h;
cin >> n >> m >> h;
vector<int> s(m + 1);
for (int i = 1; i <= m; i++) {
cin >> s[i];
}
int all = accumulate(s.begin(), s.end(), 0LL);
if (all < n) {
cout << -1 << endl;
return 0;
}
int rem = s[h] - 1, dif = all - s[h], x, y;
n--;
// dp[i][j] -> 前 i 个人中有 j 个人与自己同专业的概率
vector dp(n + 1, vector<double>(rem + 1));
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= min(rem, i); j++) {
if (j == 0) {
x = rem; // 剩下自己专业人的数量
y = dif - i + 1; // 剩下不是自己专业人的数量
dp[i][j] = dp[i - 1][j] * y / (x + y);
} else {
x = rem - (j - 1);
y = dif - (i - j);
dp[i][j] += dp[i - 1][j - 1] * x / (x + y);
x = rem - j;
y = dif - (i - 1 - j);
dp[i][j] += dp[i - 1][j] * y / (x + y);
}
}
}
double ans = 0;
for (int i = 1; i <= rem; i++) {
ans += dp[n][i];
}
cout << ans << endl;
}
代码细节非常多,比如人数需要去掉自己、\(j\) 的极限取值等等。
解法二:逆向推导
逆向推导就很简单了,不满足的情况即为剩余 \(n-1\) 个人都和自己专业不同,\(\dbinom{n-1}{all-s_h}\) ,全部情况为 \(\dbinom{n-1}{all-1}\) ,相除后用 \(1\) 减去即为所求。
1461C - Random Events \(^{*1500\text{;概率}}\)
基础概率题,学过概率的应该都能做。
1836B - Astrophysicists \(^{*1100\text{;赛、贪心、数学}}\)
某次比赛没写出来的题目。需要比较细致的推导,个人体感表面这道题难度超过 \(*1500\) ……
首先考虑最优情况,即每个人都给 \(num=\left \lceil \dfrac{g}{2} \right\rceil-1\) ,这样可以私吞 \(ans=num\cdot n\) 元。
随后分析这样做之后的可行性,有两个情况,其一是原本没有这么多钱,那么答案为将全部的钱吞光,即 \(k\cdot g\) 。而当原本的钱多于 \(ans\) 时,我们需要额外处理剩余的钱。
由题目规定,每个人多给 \(g\) 元不会影响 \(ans\) ,所以我们尽可能的凑 \(g\) 元。现在,\(\left \lfloor \dfrac{k * g - ans}{g} \right \rfloor\) 人多发到 \(g\) 元,这部分钱不会减少 \(ans\) 的值;至多 \(1\) 个人再多发到 \(extra = (k * g - ans) \bmod g\) 元,这部分的钱会减少 \(ans\) 的值——原先只需要给 \(num\) 元的人,现在要给 $num + extra $ 元,即原先私吞的金额为 \(num\) 元,现在私吞的金额为 \(num + extra - g\) 元,化简后 \(ans\) 变为 \(ans-num + num + extra - g=ans+extra -g\) 。
353D - Queue \(^{*2000\text{;dp}}\)
一开始没觉得这是dp,但是看了题解之后才发现这确实就是dp。
考虑直接计算,某个女生向前移动的步数至少为其前面的男生数量步,这是很显然的,随后我们需要特殊考虑多个女生相连的情况,由于相连时无法一起移动,所以第二个女生要比第一个女生多等待一秒,第三个女生要比第二个多等待一秒,……。
综合上述两个情况进行转移即可。
2023.07.05
1805D - A Wide, Wide Graph \(^{*1800\text{;树-直径、搜索}}\)
典题。首先明确定义(就是题目中的定义):对于一棵树 \(G\) 中的两个点,如果它们之间的距离不小于 \(k\) ,那么在子图 \(G_k\) 中这两个点也相连。
显然,我们容易得到:\(G_k\) 是森林,且如果其由 \(p\) 棵树构成,那么 \(k-1\) 棵树仅含有一个节点,剩下一棵树含 \(n-k+1\) 个节点。
随后我们思考某个点在 \(k\) 为什么的时候才会独立出去成为一棵树?可以发现,当其不与任何点相连(即到所有其他点的距离均小于 \(k\))时成立。
蒟蒻都知道的结论:对于树上任意一点,距其最远的点一定是直径的某一个端点。
至此,只需要处理出直径的两个端点即可解决上述的问题。
2023.07.04
767C - Garland \(^{*2000\text{;树、搜索}}\)
题目难度应该都在读题上,去掉读题可能只有*1300左右。另外有一个难点在于输出的时候,可以被删除的边数目可以大于 \(2\) ,且根节点的那条边一定是最后被放入答案序列的,所以只需要输出答案序列的前两个就可以。
如果 \(\color{#df0030}{\text{Wrong answer on test 9}}\),可以参考下方样例:
6
2 0
0 0
4 0
2 0
1 0
4 0
1294F - Three Paths on a Tree \(^{*2000\text{;树论-直径、搜索}}\)
虚高。树的直径模板题。比较一眼的求直径后找点,除了特判可能是个坑,其他并没有难点。
187B - AlgoRace \(^{*1800\text{;DP、图论-最短路}}\)
很恐怖的范围,想了很久。之后发现我们可以一层一层分析,首先先不看全部线路,只关心一条,这样可以用 \(\tt Floyd\) 计算得到这条线路任意两点之间的最短时间,此时,即为不换乘;随后引入别的线路,发现可以转移:记 \(dp_{i,j,k}\) 为换乘 \(k\) 次从 \(i\) 到 \(j\) 的最短时间,转移过程中再使用一次 \(\tt Floyd\) :\(dp_{i,j,k}=dp_{i,l,k-1}+dp_{l,j,0}\) 。
2023.07.02
1202D - Print a 1337-string... \(^{*1900\text{;构造}}\)
总体思路不难,但是细节比较多。
1202B - You Are Given a Decimal String... \(^{*1700\text{;图论-最短路}}\)
建图比较困难。
1706D1 - Chopping Carrots (Easy Version) \(^{*1700\text{;贪心、暴力、构造}}\)
按理来说这是道典题:上下界均不确定,所以我们人为固定一个边界,随后暴力枚举另一个边界即可。这题我们选择固定下边界:由于题目说明 \(a_1\) 是 \(a\) 序列的最小值,所以最小值取值为 \(a_{\min} \in \left[\dfrac{a_1}{k},a_1 \right]\) ,至多 \(\mathcal O(a_1)\) 种情况,随后我们发现上边界需要计算全部元素后得到,所以基础复杂度需要再乘以一个 \(\mathcal O(N)\) ,于是我们需要在接近线性的时间内计算出上边界。
众所周知,\(\log\) 的做法是很难被卡掉的,所以至此,有两个显而易见的求法,一是再乘以一个 \(\mathcal O(\log (\max a_i))\) 用二分解;一是用数论方式完全线性的求解。
这里考虑数论的解法,我们的目标是:对于每一个 \(a_{\min} \in \left[\dfrac{a_1}{k},a_1 \right]\) ,遍历整个 \(a\) 数组,对于每一个 \(a_i\) 求解最小的 \(a_{i_{\min}}=\left\lfloor \dfrac{a_i}{p_i} \right\rfloor\) 满足 \(a_{i_{\min}} \le a_{\min}\) ,可得 \(p_i\le \left\lfloor \dfrac{a_i}{a_{\min}} \right\rfloor\) ,代回后得到 \(a_{i_{\min}}\le \left\lfloor \dfrac{a_i}{\left\lfloor \dfrac{a_i}{a_{\min}} \right\rfloor} \right\rfloor\) ,至此,对答案的贡献为 \(\displaystyle \min_{a_{\min\ }=\frac{a_1}{k}}^{a_1} \left\{ \max_{i=1}^{n} \left\{ a_{i_{\min\ }} \right\}-a_{\min} \right\}\) 。
最终复杂度趋近于 \(\mathcal O(N^2)\) 或 \(\mathcal O(N^2\cdot \log N)\) 。
关于 Hard Version ,我们可以发现,每一个 \(a_{i_{\min}}\) 的形式显然是整除分块的模样,所以我们可以用预处理来降低复杂度至 \(\mathcal O(N\cdot \sqrt{N})\) ,可惜我想了好久还是没明白整除分块后每一个 \(a_{i_{\min}}\) 对答案的最终贡献,所以这里只能先放一放了。
同样的,也有一个带 \(\log\) 的做法,是使用线段树辅助处理,但是需要卡常(很显然, \(\mathcal O(N\sqrt{N}\cdot \log N)\) 非常之极限),思维难度上可能会更简单一些。
下方是 Hard Version 未完成的代码。
signed main() {
int Task = 1;
for (cin >> Task; Task; Task--) {
int n, k;
cin >> n >> k;
vector<int> a(n + 1), Max(n + 1);
int ans = numeric_limits<int>::max();
for (int i = 1; i <= n; i++) {
cin >> a[i];
// 对 P = a_i / p_i (P \in [1, k]) 进行分块,P一共有 sqrt(a[i]) 个不同取值
// 即: P \in [l, r] 时 a_i / P 的结果相同。理论复杂度 sqrt(a[i])
for (int l = 1, r; l <= min(k, a[i]); l = r + 1) { // 小优化:k>=l>a[i]的时候都是0,直接跳过
r = a[i] / (a[i] / l); // 整除分块板子
}
}
cout << ans << endl;
}
}
156D - Clues \(^{*2500\text{;图论-Prüfer 序列、组合数学}}\)
需要使用 \(\tt Prüfer\) 序列推导出凯莱公式,随后使用多元二项式定理再推导化简。
2023.06.30
1845C - Strong Password \(^{赛}\)
赛时一开始想到搜索加剪枝,但是好像在极限情况下不对,但是没管直接写了,结果因为递归的过程中多递归了一个 \(\tt string\) 导致超时,赛后改出来了,但是官方样例里面没有上述提到的极限情况,所以被hack了。
补题时发现这题其实用不上搜索,直接用 \(\tt dp\) 就能做……已经连续两场卡 \(\tt dp\) 题了,需要好好补一下。
2023.06.24
1249D2 - Too Many Segments (hard version) \(^{*1800\text{;数据结构-堆、贪心}}\)
对于这种区间覆盖问题大部分情况是贪心,小部分情况是DP,还有极少部分是网络流。—— @Binary_Search_Tree
本题使用贪心+模拟的过程处理,这个贪心应该比较套路,即——要删除线段时,先删除右端点更大的线段,这样可以减少其对后面点的影响。其他没什么,看看代码应该就会做了。
2023.06.23
期末周课设周结束了,恢复刷题的第一天。
484B - Maximum Value \(^{*2100\text{;复杂度欺骗}}\)
这是一题复杂度欺骗题。我们对于每一个 \(a_i\) ,枚举它的倍数,随后对于每一个倍数,二分找到小于其的第一个数,然后更新答案。
随后我们考虑优化,(1)限制倍数的范围是非常显然的,上下界分别为:\(\left[2,\left\lceil \dfrac{a_n}{a_i} \right\rceil \right]\);(2)相同数字显然没必要计算两遍,故去重;(3)此时最大的复杂度问题在于较为小的数字,它们的倍数相当的多,但是相应的它们能构造得到的答案也较小,所以我们倒置数组进行枚举。
本题数据是随机构造的,不进行(3)已经可以卡过去,优化全部加上后可以在 \(0.1s\) 内跑过,效率非常高。
int upp(int x, int y) { return (ceil)(1.0 * x / y); } // 上整除
bool Solve() {
int n;
cin >> n;
vector<int> a(n);
for (auto &it : a) {
cin >> it;
}
sort(a.begin(), a.end());
a.erase(unique(a.begin(), a.end()), a.end());
n = a.size();
int ans = 0;
for (int i = n - 1; i >= 0; i--) {
for (int j = 2; j <= upp(a[n - 1], a[i]); j++) { // 枚举倍数
if (a[i] < ans) { // 剪枝
continue;
}
auto val = lower_bound(a.begin(), a.end(), a[i] * j);
if (val == a.begin()) {
continue;
}
ans = max(ans, *--val % a[i]);
}
}
cout << ans << endl;
return 0;
}
474F - Ant colony \(^{*2100\text{;数论、数据结构:线段树}}\)
性质很容易想到,就是求区间内有多少个值等于区间 \(\gcd\) ,进一步,如果这样的元素的数量不为零,那么一定等价于:区间内有多少个值等于区间最小值。
整理需要处理的内容:区间 \(\gcd\) 、区间最小值、区间最小值的数量。可以使用一棵线段树一步到位,当然,也可以用 \(\tt ST\) 表、莫队、\(\tt STL\) 来计算出上方的某一个或几个值,但是都没有线段树那么优雅。
另一方面,看到有用线段树重载运算符同步处理上面三个值的,这次写没学,直接手搓了三个询问函数搞定的。如果再碰到这个技巧可以学习一下。
2023.06.18
1834E - MEX of LCM \(^{赛}\)
这个数据范围加上LCM的性质,很容易想到这题是一个复杂度欺骗题。由于现在题解还没出,我就我赛时的想法梳理一下:题目所给条件计算能够得到的值是非常有限的,所以,我们干脆把全部的值全给算出来,然后暴力寻找答案即可。但是这样会计算出非常大的值,所以这里还有一个保证复杂度的内容,在于统计的上限为 \(10^9\) (jiangly在这里给出的限定是 \(20\cdot n\) ,群友说判到 \(2\cdot n\) 就可以了……),对于超过这个限定值的值我们全部排除即可。
这个想法的准确性暂时不得而知,可能与 \(\tt{lcm} \rm{\{1,2,3,\dots,20\}}\) 相关等我之后更新。
1834D - Survey in Class \(^{赛}\)
显然,我们发现需要分别维护左相交、右相交和包含这样三种情况,这个很好想,但是具体该怎么做呢?赛时想了一个多小时都没搞定(虽然后半程就往离散化+某些东西维护上面想了,但是群友说这个方法确实能写,就是代码比较美丽),赛后群友说是经典套路……
看过jiangly的代码之后确实感觉这个比较典。
2023.06.17
486D - Valid Sets \(^{*2100\text{;树形dp}}\)
比较巧妙,条件是差值,这代表上下界均不确定,于是这里采用固定上/下界后枚举其他所有点判差值的方式进行DP转移,比较典,代价是 \(\mathcal O(N^2)\) 。
还有一个需要注意的地方是存在相同权值的点,因为要统计数量,所以要找一个不重不漏的方法进行计算。
837D - Round Subset \(^{*2100\text{;dp}}\)
二维费用背包,加上一定数学计算,接近于板子。
例题:从 \(N\) 个数字中任选 \(M\) 个,使得这 \(M\) 个数字的 $\min {Sum_{\text{因数2的数量}},Sum_{\text{因数5的数量}}} $ 最大。使用 dp[j][k] 表示选取了 \(j\) 个数, \(Sum_{\text{因数5的数量}}=k\) 时的最大 \(Sum_{\text{因数2的数量}}\) See 。
bool Solve() {
int n, m;
cin >> n >> m;
vector<int> a(n + 1), val2(n + 1), val5(n + 1);
for (int i = 1; i <= n; i++) {
cin >> a[i];
int x = a[i];
while (x % 2 == 0) {
x /= 2;
val2[i]++;
}
while (x % 5 == 0) {
x /= 5;
val5[i]++;
}
}
int sum = accumulate(val5.begin(), val5.end(), 0LL);
vector<vector<int>> dp(m + 1, vector<int>(sum + 1, -INF));
dp[0][0] = 0;
for (int i = 1; i <= n; i++) { // 当前选择第i个元素
for (int j = m; j >= 1; j--) { // 前i个元素选择了j个
for (int k = sum; k >= val5[i]; k--) { // 5的数量
dp[j][k] = max(dp[j][k], dp[j - 1][k - val5[i]] + val2[i]);
}
}
}
int ans = 0;
for (int k = 0; k <= sum; k++) {
ans = max(ans, min(k, dp[m][k]));
}
cout << ans << endl;
return 0;
}
2023.06.14
700B - Connecting Universities \(^{*1800\text{;树论、dp}}\)
非常精彩的贪心(?)题,题解都说是贪心那就是贪心吧。这题的巧妙之处在于使用边来分割整张图成为两部分,这样一来就把点的问题转化为联通的问题,进而转化为边上问题。
感觉这个思路是个典,所以写入了典题列表。
1829H - Don't Blame Me \(^{*1700\text{;dp、位运算}}\)
好简单的题……赛时想了好久都没写出来,这次补位运算专题才发现这题极其简单,但是由于我对这两个标签都不熟悉,所以赛时没这个信心一定能给它写出来。还是要提振一下信心的。
2023.06.13
1559D2 - Mocha and Diana (Hard Version)
\(\tt DSU\) 的另类用法:选取中心点作为特殊点,连边保证连通性。
2023.06.11
1304D - Shortest and Longest LIS \(^{*1800\text{;构造}}\)
天才般的构造!对称的极致美学(可能是典,但是我第一次见到)。
2023.06.09
1368D - AND, OR and square sum
个人感觉这题有两个解题思路。
其一是,我们需要发现题目中给定的操作只会将 \(x\) 二进制模式下的全部 \(1\) 移动到 \(y\) 的对应位置上。这个规律可以打表得到,如下图:
bool Solve() {
int A, B;
cin >> A >> B;
bitset<10> x = A;
bitset<10> y = B;
_(x);
_(y);
_(x|y);
_(x&y);
return 0;
}
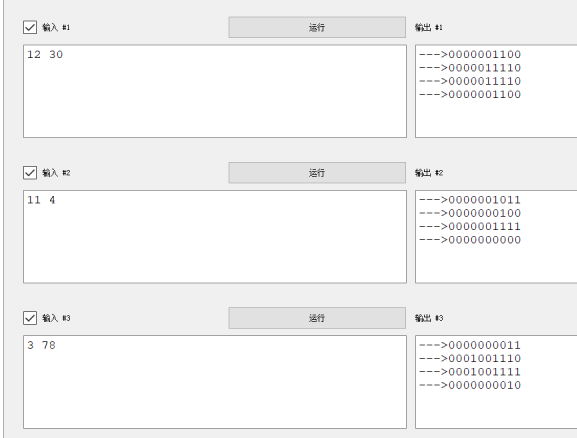
这有什么用呢?这说明 \(1\) 是可以无损移动的,那么我们尽可能让 \(a_i\) 的大小差距拉开(大的尽可能大、小的尽可能小),就可以使得所求最大。
第二个做法更不容易想到,如下。首先,位运算有个公式:\(x+y=x|y+x\&y\) 。根据这个公式我们可以知道,题目中定义的操作不会影响 \(\displaystyle\sum_{i=1}^n a_i\) 的值。
那么,问题在于 \(\displaystyle\sum_{i=1}^n a_i\) 和我们要求解的式子有什么关系呢……显然,根据高中数学,我们有公式 \(\displaystyle\sum_{i=1}^n a_i^2 =(\sum_{i=1}^n a_i)^2-2\cdot \sum_{i=1}^{n}\sum_{j=i+1}^{n}a_ia_j\) ,此时已知操作不会改变 \(\displaystyle(\sum_{i=1}^n a_i)^2\) 的值,所以要使得 \(\displaystyle\sum_{i=1}^n a_i^2\) 最大,即要让 \(\displaystyle\sum_{i=1}^{n}\sum_{j=i+1}^{n}a_ia_j\) 最小。
现在的问题变成了怎样分配 \(a_i\) ,使得 \(\displaystyle\sum_{i=1}^{n}\sum_{j=i+1}^{n}a_ia_j\) 最小,我们发现,当 \(0\) 的数量最多时,乘积也有最多的 \(0\) 。所以,我们需要让 \(a_i\) 的大小差距拉开。
2023.04.26 \(^{9\text{;*2000乱刷}}\)
1716D - Chip Move \(^{*2000\text{;DP优化}}\)
容易发现,由于 \(k\) 这一限制的存在,一轮最多转移 \(\mathcal O(\sqrt{N})\) 次,于是,一个单轮复杂度 \(\mathcal O(N\sqrt{N})\) 的DP转移跃然纸上:\(dp_{i,j}\) 代表跳了 \(i\) 次后位于 \(j\) 位置的方案数。
那么,面对多轮问题时,前缀和优化是很容易被想到的,且显然,这道题是可以使用这一优化的,于是,多轮复杂度也为 \(\mathcal O(N\sqrt{N})\) ,可以过题。但是有一个小差异在于,这题的前缀和并不是连续的,所以,在处理时需要多留一个心眼。\(pre_{i,j}\) 代表跳 \(i\) 次后位于 \(j\) 位置的方案数之和。
最后分析空间复杂度,发现以现在的定义一定会出事,考虑优化。pre 数组可以直接压缩为一维;而 dp 数组由于中途需要用于更新 pre 数组,故使用滚动数组替代。我们能够很方便的写出如下代码:
vector<Z> dp0(n + 1), ans(n + 1), pre(n + 1);
dp0[0] = 1;
for (int i = 1; i <= m; i++) {
vector<Z> dp(n + 1);
for (int j = 0; j <= n; j++) {
pre[j] = dp0[j];
if (j >= k + i - 1) {
pre[j] += pre[j - (k + i - 1)];
dp[j] = pre[j - (k + i - 1)];
ans[j] += dp[j];
}
}
dp0 = dp;
}
如果你的常数略大——很不幸,您T了。我们分析这样写的精确复杂度,即便不考虑内层循环中的操作复杂度,总复杂度也会来到 \(\mathcal O(\sqrt{N} \cdot 3N)\) 的层级。当 \(N_{MAX}=2\cdot 10^5\) 时,需要计算 \(3\cdot 10^8\) 次,这是非常危险的。
我们考虑优化滚动数组。回忆刚刚的分析,“dp 数组由于中途需要用于更新 pre 数组,故使用滚动数组替代”,故我们强制在本轮更新掉整个 pre 数组即可。
vector<Z> dp(n + 1), ans(n + 1), pre(n + 1);
dp[0] = 1;
for (int i = 1; i <= m; i++) {
for (int j = 0; j <= n; j++) {
Z val = 0;
if (j >= k + i - 1) {
val += pre[j - (k + i - 1)];
}
pre[j] = val + dp[j]; // 借助val强制更新整个pre数组
dp[j] = val;
ans[j] += dp[j];
}
}
最后补充两点做这题时遇到的问题:
GNU C++20 (64)跑DP的速度比GNU C++17快一倍,直接是AC和超时的区别!
Zmod类速度与手动取模不相上下,不要再觉得超时是类导致的了,其实效率极高。
2023.04.25 \(^{9\text{;*2000乱刷}}\)
两个小时多一点点六题*2000……即便最近刷题这么多,还是感到很吃惊。
个人总结,和此前结论一致——*2000分段有一个极其显著的特点是,题目代码都不太长,且总给我一种虚高的感觉,并没有遇到过特别坑的题目,以思维+贪心为主。暂时主观评价这样,等过几日我刷的题多了再做二轮评价。
1296E2 - String Coloring (hard version) \(^{*2000\text{;DP}}\)
由于实在没题目总结了,把这道题搬上来。总体感觉并没有DP思想,且与easy版本思维差距极小,如果先做easy版本很容易就被带歪思路。
当然也可以拥抱DP,用最长下降子序列的思路解这道题,和正解大差不差,由于我DP并不好,所以直接没有管这个。留坑,看会不会填。
710E - Generate a String \(^{*2000\text{;DP}}\)
转化成跳方格这一经典问题。列出转移方程(但不是最终的答案方程)。
注意当 \(n\) 为奇数时的第二种情况是由 \(\left \lfloor \frac{n+1}{2} \right \rfloor\) 先乘二转移到 \(n+1\) 、再减一转移而来。
(典)注意到当 \(n\) 为偶数时没有从 \(n+1\) 转移过来的情况,而这也是这个线性DP复杂度正确的关键,那么为什么呢。这里记 \(u\) 为偶数、\(v=u+1\) ,考虑 \(F_v\) ,其必然不会从 \(F_u\) 转移而来,而会从 \(F_{\left \lfloor \frac{v+1}{2} \right \rfloor}\) 转移,其代价等价于直接从 \(F_{\left \lfloor \frac{u}{2} \right \rfloor}\) 转移,为 \(x+y\) 。故可以略去这一步转移,得到线性递推方程。
2023.04.24 \(^{6\text{;主要集中于*1900的区间DP题}}\)
另这一晚有Div3,小做了几道。
区间DP专题:P4170 [CQOI2007]涂色
特点在于,如果某个区间左端和右端颜色一致,那么 dp[l][r] = min(dp[l + 1][r], dp[l][r - 1]) 转移过来。原因在于,既然一个端点的颜色是这个,那么在涂这个端点的时候完全可以顺手把另一个端点也一起涂了,这样是不需要额外的操作步骤的,其余与标准区间DP一致。
区间DP专题:1132F - Clear the String \(^{*2000\text{;DP}}\)
虚高题,顶天*1600了。特点在于,如果某个区间左端和右端颜色一致,那么删除次数需要 \(-1\) 。原因显而易见,这段可以一起删掉。
区间DP专题:P3847 [TJOI2007]调整队形
特点在于,环形数组,倍增后处理即可;其次特点还在于,每个区间都是有初始值的。
区间DP专题:149D - Coloring Brackets \(^{*1900\text{;DP}}\)
因为条件有“相邻两个括号颜色不能相同”,所以采用了思维数组,但是判断比较麻烦,所以这里这种采用了记忆化递归的方式进行。总体来说与区间DP模板关系不大,属于较为独立的题目。
区间DP专题:1572C - Paint \(^{*2700\text{;DP}}\)
《涂色》的逆向加强版,难度虚高,但是以我的理解暂时说不出过程,所以先留坑。
478D - Red-Green Towers \(^{*2000\text{;DP}}\)
比较好想的递推题(也可以理解为DP,但是我总感觉沾上DP之后心理作用会觉得题目难度上升了),容易想到的是用 \(F_{i,j,k}\) 分别代表在第 \(i\) 层使用了 \(j\) 个红块和 \(k\) 个绿块的方案数量,但是显然这是不可行的,因为空间超了。于是尝试优化,发现每层数量固定、红块数量已知的情况下可以推出绿块数量,于是减少一维;新一层方案数只与上一层相关,于是用滚动数组再减少一维,得解。
本题洛谷题解写的很别扭,明明很清晰的一道题整的非常曲折;于是我参考了Jimanbanashi的思路,大佬写的非常清晰,好评。
2023.04.23 \(^{11\text{;主要集中于*1900的几何题}}\)
1656D - K-good \(^{*1900\text{;数论}}\)
首先我们发现连续的 \(k\) 个数一定满足“余数各不相同”这一条件,随后我们尝试证明:如果有解,则一定可以转换为连续的 \(k\) 个数之和(不懂严格证明,这里就不写出来了)。
经过证明,我们可以根据等差数列 \(p,(p+1),\dots,(p+k-1)\) 得到公式 \(n=\dfrac{(p + p + k - 1) \cdot k}{2}=pk +\dfrac{k(k-1)}{2}\) 。随后,我们用到一个典:分析奇偶性。
对上式变形:\(2\cdot n=k\cdot(2p+k-1)\) ,我们可以发现,左边一定为偶数,右边为一个奇数乘以一个偶数,那么我们如果将\(2\cdot n\) 里的全部 \(2\) 都取出来,那么左边也能变成一个奇数乘以一个偶数的形式。而又因为右边 \(k<2p+k-1\) ,所以左边变形后得到的较小的那个数即为 \(k\) 。
举例:\(20=2^2*5\) ,那么 \(k=2^2,(2p+k-1)=5\) 。之所以是典是因为这样做的复杂度为 \(\mathcal O(\log N)\) 。
bool Solve() {
int n; cin >> n;
int x = 2;
while (n % 2 == 0) {
n /= 2;
x *= 2;
}
int k = min(n, x);
cout << (k >= 2 ? k : -1) << endl;
return 0;
}
1430E - String Reversal \(^{*1900\text{;数据结构}}\)
某种程度上可以看作是典题。容易发现,逆序对的数量是一个可行解,但不是最优解。
观察第三组样例:
icpcsguru
123456789
对于相同的一对 u 和 c ,最优方案一定是不对其进行交换,于是翻转后,我们需要对相同字符对的下标进行修改,使得小的下标在前面,大的下标在后面。
修改前
urugscpci
987654321
修改后
urugscpci
789654321
这样的修改带来的好处是显而易见的,小的数据在前可以最大程度的减少逆序对的数量。最后,对于修改后的下标计算逆序对数量即可。
另补充一组数据:
4
puut
答案为 \(5\) ,当你意识到数据中的这一对 u 对于答案的意义所在,本题即能轻松化解。
342C - Cupboard and Balloons \(^{*1900\text{;几何}\)
不考虑半圆部分,我们发现,最多可以放置 \(\left\lfloor \dfrac{h}{r} \right\rfloor\cdot 2\) 个气球,此时,矩形部分剩余的空白高度为 \(H=h-\left\lfloor \dfrac{h}{r} \right\rfloor\cdot r\) 。
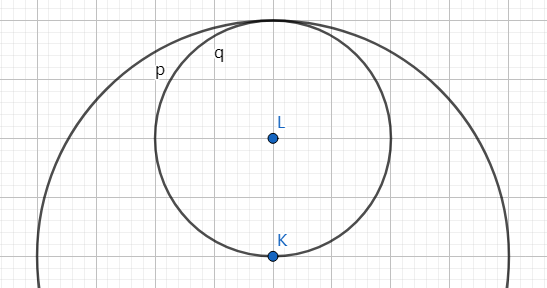
随后我们考虑半圆部分,如上图所示,一定可以放下至少一个气球,那么,能否放下两个气球呢?

如上图所示,当 \(H > \dfrac{r}{2}\) 时可以放下两个气球。
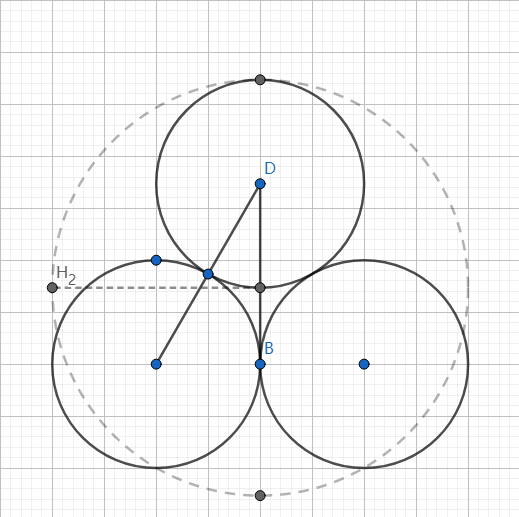
最后我们观察放下三个气球的情况,如上图所示,线段DB的值与 \(H\) 等价,故当 \(H^2>r^2+\dfrac{h}{2}^2\) 时可以放下三个气球。
bool Solve() {
int r, h; cin >> r >> h;
int H = h - h / r * r, ans = h / r * 2 + 1;
if (H * 2 >= r) ans++;
if (4LL * H * H >= 3LL * r * r) ans++;
cout << ans;
return 0;
}
1163C2 - Power Transmission (Hard Edition) \(^{*1900\text{;几何}\)
要求解决如下几个问题:
- 对于给定的互不不相同的点,两两组合,求解出它们能组出的不同的直线数量;
- 对于计算得到的不同的直线,两两组合,求解出有多少对直线间有交点。
对于Easy版本,给出至多 \(50\) 个点,能组合出至多 \(250\) 条直线,允许 \(\mathcal O(N^2)\) 的算法通过。所以我们暴力计算出全部的直线,然后两两组合,使用叉乘判断是否平行即可。
对于Hard版本,能组合出至多 \(10^6\) 条直线,故需要进行优化,这里我直接储存斜率并计算,以 \(\mathcal O(N)\) 的复杂度通过。
总体来说,如果是初学几何,Hard版本的思路可能比Easy版的更容易想到,因为Easy版本的更为模板。而两个版本算法的本质都是围绕直线的两点式、一般式公式的转换以及斜率的计算所展开的。总的来说,本题两个版本的解法都非常有趣,同时重要的是模板的积累。
这里罗列一下使用到的模板,在此感谢 \(\mathcal Hamine\) 的几何模板整理。
using i64 = long long;
const double eps = 1e-8;
struct point {
i64 x, y;
point operator+(const point &p) const { return point{x + p.x, y + p.y}; }
point operator-(const point &p) const { return point{x - p.x, y - p.y}; }
point operator*(i64 t) const { return point{x * t, y * t}; }
point operator/(i64 t) const { return point{x / t, y / t}; }
friend auto &operator<<(ostream &o, const point &j) {
return o << j.x << " " << j.y;
}
friend bool operator<(const point &i, const point &j) {
return (i.x != j.x ? i.x < j.x : i.y < j.y);
}
};
i64 dis(point p1, point p2) { // 曼哈顿距离公式
return abs(p1.x - p2.x) + abs(p1.y - p2.y);
}
double cross(point p1, point p2) { // 叉乘
return p1.x * p2.y - p1.y * p2.x;
}
int sign(double k) {
if (k > eps) return 1;
else if (k < -eps) return -1;
else return 0;
}
bool parallel(point p1, point p2, point p3, point p4) { // 判断是否平行
return sign(cross(p1 - p2, p3 - p4)) == 0;
}
auto getfun(point p1, point p2) { // 两点式转换为一般式
int A = p1.y - p2.y, B = p2.x - p1.x, C = p1.x * A + p1.y * B;
if (A < 0) A = -A, B = -B, C = -C;
else if (A == 0)
if (B < 0) B = -B, C = -C;
else if (B == 0 && C < 0) C = -C;
if (A == 0) {
if (B == 0) C = 1;
else {
int g = gcd(abs(B), abs(C));
B /= g, C /= g;
}
} else if (B == 0) {
int g = gcd(abs(A), abs(C));
A /= g, C /= g;
} else {
int g = gcd(gcd(abs(A), abs(B)), abs(C));
A /= g, B /= g, C /= g;
}
return tuple{A, B, C};
}
bool same(point p1, point p2, point p3, point p4) { // 判断两条直线是否是同一条
return getfun(p1, p2) == getfun(p3, p4);
}
point intersection(point p1, point p2, point p3, point p4) { //两直线交点
double w1 = cross(p1 - p2, p4 - p2);
double w2 = -cross(p1 - p2, p3 - p2);
return (p3 * w1 + p4 * w2) / (w1 + w2);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号