知识点整理——图上的环(判环、求解最小环)
前言
近日刷图论题遇到了多道求解最小环的例题,由于方法众多,用法不尽相同,数次被此所困扰。在互联网上寻找良久,却没能发现什么系统性的整理,所以便有了此文。
求解此类问题:
给出一张图,输出图中最小环的大小。定义最小环为:由 \(k(k \ge 3)\) 个点构成的最小的简单环。
三元环相关模板
定义
很显然,三元环也属于简单环,所以简单环里面的算法依旧是可以使用的。
性质:若一张有向完全图存在环,则一定存在三元环。
完全图输出三元环上元素
| 有向图 | 无向图 |
|---|---|
| ✔ | ✔ |
时间复杂度为 \(\mathcal O(N^2)\) 。
详解
这部分的代码来自这一道题目,题目大意为:给出一张有向完全图,输出任意一个三元环上的全部元素。
下方的代码同样适用于非完全图和无向图(但是我个人没有测试过)。
bool Solve() {
int n; cin >> n;
vector<vector<int> > a(n + 1, vector<int> (n + 1));
for (int i = 1; i <= n; ++ i) {
for (int j = 1; j <= n; ++ j) {
char x; cin >> x;
if (x == '1') a[i][j] = 1;
}
}
vector<int> vis(n + 1);
function<void(int, int)> dfs = [&] (int x, int fa) {
vis[x] = 1;
for (int y = 1; y <= n; ++ y) {
if (a[x][y] == 0) continue;
if (a[y][fa] == 1) {
cout << fa << " " << x << " " << y;
exit(0);
}
if (!vis[y]) dfs(y, x); // 这一步的if判断很关键
}
};
for (int i = 1; i <= n; ++ i) {
if (!vis[i]) dfs(i, -1);
}
cout << -1;
return 0;
}
最小环相关模板
输出图上最小环大小(其一): \(\tt flody\)
应用极为广泛的做法,本质是求出最短路后暴力枚举。泛用性高、代码短,唯一的缺点是时间复杂度较高,为 \(\mathcal O(N^3)\) 。
| 有向图 | 无向图 |
|---|---|
| ✔ | ✔ |
| 判断是否存在 | 输出数量 | 输出大小 | 输出环上元素 | |
|---|---|---|---|---|
| 最小环 | ✔ | ✔ | ||
| 简单环 | ✔ | ✔ | ||
| 环 | ✔ | ✔ |
详解
这部分的代码来自这一道题目,题目大意为:给出一张无向图,求解该图最小环的大小。
int flody(int n) {
for (int i = 1; i <= n; ++ i) {
for (int j = 1; j <= n; ++ j) {
val[i][j] = dis[i][j]; // 记录最初的边权值
}
}
int ans = 0x3f3f3f3f;
for (int k = 1; k <= n; ++ k) {
for (int i = 1; i < k; ++ i) { // 注意这里是没有等于号的
for (int j = 1; j < i; ++ j) {
ans = min(ans, dis[i][j] + val[i][k] + val[k][j]);
}
}
for (int i = 1; i <= n; ++ i) { // 往下是标准的flody
for (int j = 1; j <= n; ++ j) {
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
}
}
return ans;
}
输出图上最小环大小(其二): \(\tt bfs\)
复杂度 \(\mathcal O(N^2)\) 。
| 有向图 | 无向图 |
|---|---|
| ✔ | ✔ |
| 判断是否存在 | 输出数量 | 输出大小 | 输出环上元素 | |
|---|---|---|---|---|
| 最小环 | ✔ | ✔ | ||
| 简单环 | ✔ | ✔ | ||
| 环 | ✔ | ✔ |
详解
这部分的代码同样来自这一道题目,题目大意为:给出一张无向图,求解该图最小环的大小。
本质也是求解最短路。
auto bfs = [&] (int s) {
queue<int> q; q.push(s);
dis[s] = 0;
fa[s] = -1;
while (q.size()) {
auto x = q.front(); q.pop();
for (auto y : ver[x]) {
if (y == fa[x]) continue;
if (dis[y] == -1) {
dis[y] = dis[x] + 1;
fa[y] = x;
q.push(y);
}
else ans = min(ans, dis[x] + dis[y] + 1);
}
}
};
for (int i = 1; i <= n; ++ i) {
fill(dis + 1, dis + 1 + n, -1);
bfs(i);
}
cout << ans;
简单环相关模板
输出图上简单环数量:状压 \(\tt dp\)
例题地址,复杂度 \(\mathcal O(M*2^N)\) 。
| 有向图 | 无向图 | |
|---|---|---|
| 有边权 | ✔ | ✔ |
| 无边权 | ✔ | ✔ |
| 判断是否存在 | 输出数量 | 输出环上元素 | 输出大小 | |
|---|---|---|---|---|
| 简单环 | ✔ | ✔ | ||
| 最小环 | ||||
| 环 |
输出图上任意一个简单环: \(\tt dfs\) 序
本方法在本质上是使用了 \(\tt dfs\) 序加以处理,与 \(\tt tarjan\) 相仿。
| 有向图 | 无向图 |
|---|---|
| ✔ | ✔ |
| 判断是否存在 | 输出数量 | 输出大小 | 输出环上元素 | |
|---|---|---|---|---|
| 最小环 | ||||
| 简单环 | ✔ | ✔ | ✔ | |
| 环 | ✔ | ✔ | ✔ |
详解
这部分的代码来自这一道题目,处理过后的题目大意为:给出一张无向图,输出任意一个大小 \(\le K\) 的简单环上的全部元素。
注意限定:是简单环而不是最小环。
时间仓促,直接引用做题时的截图为例,在下图中,最小环为 \(2-6-5-2\) ,而使用 \(\tt dfs\) 会输出 \(2-3-4-5-6-2\) 这个简单环。
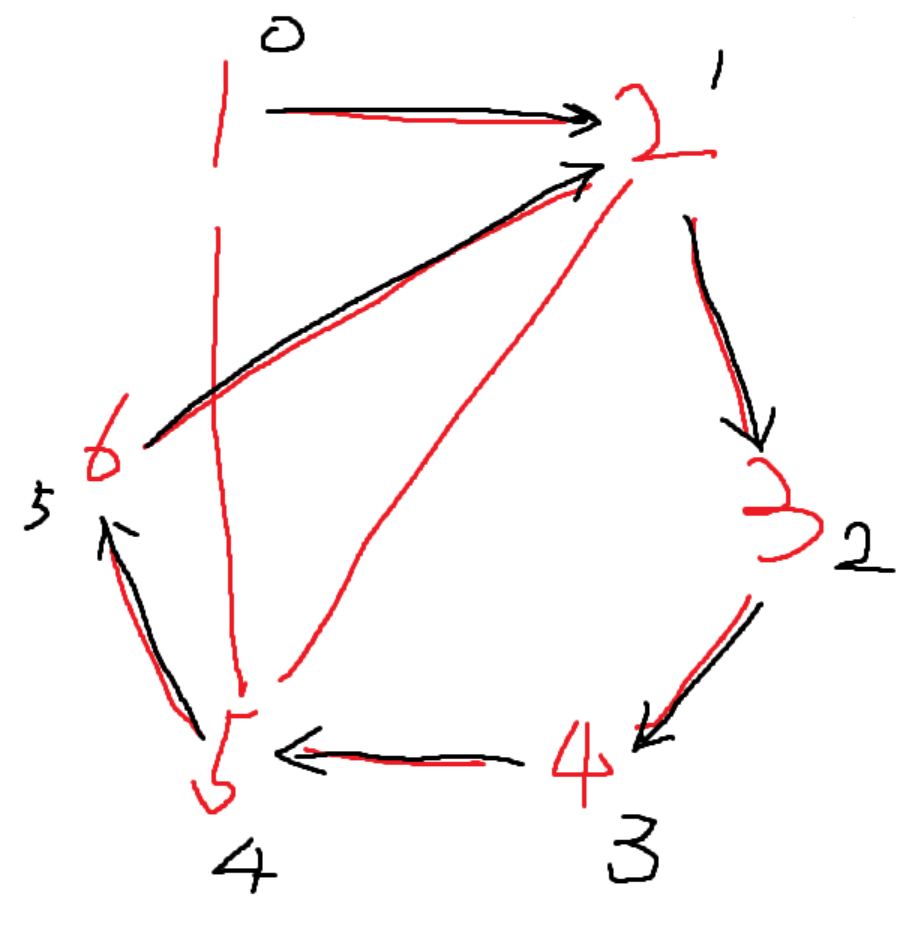
虽然这个做法不能找到最小环,但是由于其优秀的复杂度,在某些题目的解题过程中是必不可少的。
function<void(int, int)> dfs = [&] (int x, int f) {
for (auto y : ver[x]) {
if (y == f) continue;
if (dis[y] == -1) {
dis[y] = dis[x] + 1;
fa[y] = x;
dfs(y, x);
}
else if (dis[y] < dis[x] && dis[x] - dis[y] <= k - 1) { // 遇到了更小的时间戳
cout << dis[x] - dis[y] + 1 << endl; // 输出简单环的大小
int pre = x;
cout << pre << " "; // 输出环上元素
while (pre != y) {
pre = fa[pre];
cout << pre << " ";
}
exit(0);
}
}
};
dis[1] = 0;
dfs(1, -1);
输出有向图简单环大小
方法1:\(\tt dfs\) 染色
这部分的代码来自这一道题目,处理过后的题目大意为:给出一个基环内向森林,输出全部简单环的大小。这里有一点要补充的内容,即本题其实是一张无向图,但是
标准的 \(\mathcal O(N+M)\) 的 \(\tt dfs\) ,借助深度数组 dis[] 计算。
| 有向图 | 无向图 |
|---|---|
| ✔ |
| 判断是否存在 | 输出数量 | 输出大小 | 输出环上元素 | |
|---|---|---|---|---|
| 最小环 | ||||
| 简单环 | ✔ | ✔ | ||
| 环 | ✔ | ✔ |
vector<int> vis(n + 1), dis(n + 1), ring;
function<void(int)> dfs = [&] (int x) {
vis[x] = 1;
for (auto y : ver[x]) {
if (vis[y] == 0) {
dis[y] = dis[x] + 1;
dfs(y);
}
else if (vis[y] == 1) {
ring.push_back(dis[x] - dis[y] + 1);
}
}
vis[x] = 2;
};
for (int i = 1; i <= n; ++ i) {
if (!vis[i]) dfs(i);
}
for (auto it : ring) {
cout << it << " ";
}
环相关模板
判断图上是否存在环: \(\tt topsort\)
有向图与无向图都可以处理,但是判断条件略有不同。
| 有向图 | 无向图 | |
|---|---|---|
| 有边权 | ✔ | ✔ |
| 无边权 | ✔ | ✔ |
| 判断是否存在 | 输出大小 | 输出环上元素 | |
|---|---|---|---|
| 简单环 | |||
| 最小环 | |||
| 环 | ✔ |
判断有向图是否存在环:\(\tt dfs\) 染色
初始时所有点颜色均为 \(0\) ,开始对这个点进行 \(\tt dfs\) 前将其染为 \(1\) ,当结束对这个点的 \(\tt dfs\) 时将其染为 \(2\) 。当在 \(\tt dfs\) 的过程中遇到 \(1\) 时说明存在环。
| 有向图 | 无向图 | |
|---|---|---|
| 有边权 | ✔ | ? |
| 无边权 | ✔ | ? |
| 判断是否存在 | 输出大小 | 输出环上元素 | 输出数量 | |
|---|---|---|---|---|
| 简单环 | ||||
| 最小环 | ||||
| 环 | ✔ | ? | ? | ✔ |
function<void(int)> dfs(int x) {
vis[x] = 1;
for (auto y : ver[x]) {
if (vis[y] == 0) dfs(y); //如果未被搜索过
else if (vis[y] == 1) ++ ans; //如果已经被搜索过,说明找到了一个环
}
vis[x] = 2;
};
for (int i = 1; i <= n; ++ i) if (vis[i] == 0) {
dfs(i);
}
cout << ans;
判断无向图是否存在环:\(\tt dsu\)
\(\tt dsu\) 判断新连接的两个点是否具有同一祖先(直接运行 same 函数)。
| 有向图 | 无向图 | |
|---|---|---|
| 有边权 | ✔ | |
| 无边权 | ✔ |
| 判断是否存在 | 输出大小 | 输出环上元素 | |
|---|---|---|---|
| 简单环 | |||
| 最小环 | |||
| 环 | ✔ | ? | ? |
输出有向图环上元素:\(\tt tarjan\)
| 有向图 | 无向图 | |
|---|---|---|
| 有边权 | ✔ | |
| 无边权 | ✔ |
| 判断是否存在 | 输出数量 | 输出环上元素 | 输出大小 | |
|---|---|---|---|---|
| 简单环 | ||||
| 最小环 | ||||
| 环 | ✔ |
namespace SCC { // 在有向图中将强连通分量缩点后重建图
vector<PII> ver[N];
int time[N], time_cnt, upper[N];
int color[N], color_cnt;
stack<int> S; int v[N];
void clear(int n) {
for (int i = 1; i <= n; ++ i) {
ver[i].clear();
v[i] = time[i] = upper[i] = color[i] = 0;
}
time_cnt = color_cnt = 0;
while (!S.empty()) S.pop();
}
void add(int x, int y, int w) { ver[x].push_back({y, w}); }
void tarjan(int x) {
time[x] = upper[x] = ++ time_cnt;
S.push(x); v[x] = 1; // v数组用于记录x点此时是否在S中
for (auto [y, w] : ver[x]) {
if (!time[y]) {
tarjan(y);
upper[x] = min(upper[x], upper[y]);
}
else if (v[y] == 1) upper[x] = min(upper[x], time[y]);
}
if (upper[x] == time[x]) {
int pre = 0; ++ color_cnt; // colorCnt代表强连通分量的数量
do {
pre = S.top(); S.pop();
v[pre] = 0;
color[pre] = color_cnt; // 给相同强连通分量内的点染色
} while (pre != x);
}
}
void solve(int n, function<void(int, int, int)> add) {
for (int i = 1; i <= n; ++ i) { // 若原图不连通
if (time[i] == 0) tarjan(i);
}
//基于已染的颜色和附加条件重建图
for (int x = 1; x <= n; ++ x) {
for (auto [y, w] : ver[x]) {
int X = color[x], Y = color[y];
if (X != Y) add(X, Y, w); //【这里很容易写错】
}
}
}
} // namespace SCC
来点例题
抽屉原理+最小环+性质特判 在求解最小环这块属于模板题,使用 \(\tt flody\) 和 \(\tt bfs\) 均可求解。
判简单环+输出简单环+构造 使用 \(\tt dfs\) 查找并输出简单环。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号