统计学——复习笔记
算数平均数计算
加权算术平均数
其中,\(x_i\) 表示各组平均水平值,\(f_i\) 代表频数。
例题
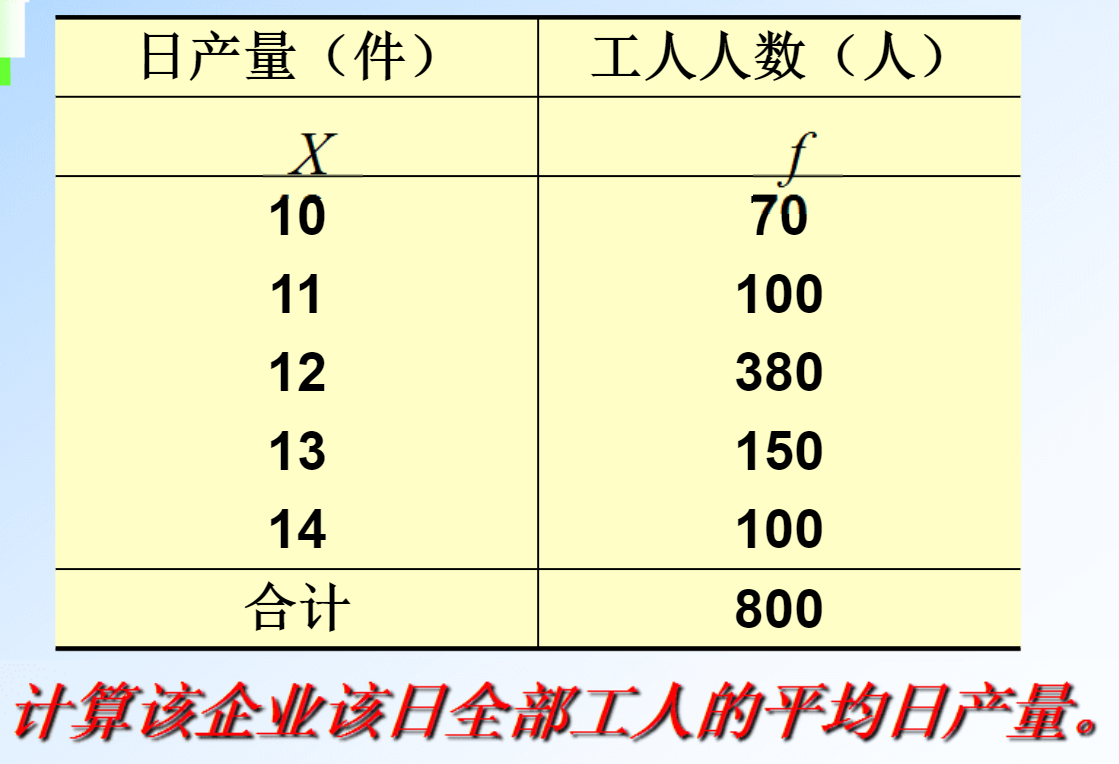
调和平均数(倒数平均数)
先取倒数再计算。
例题
加权调和平均数
例题1
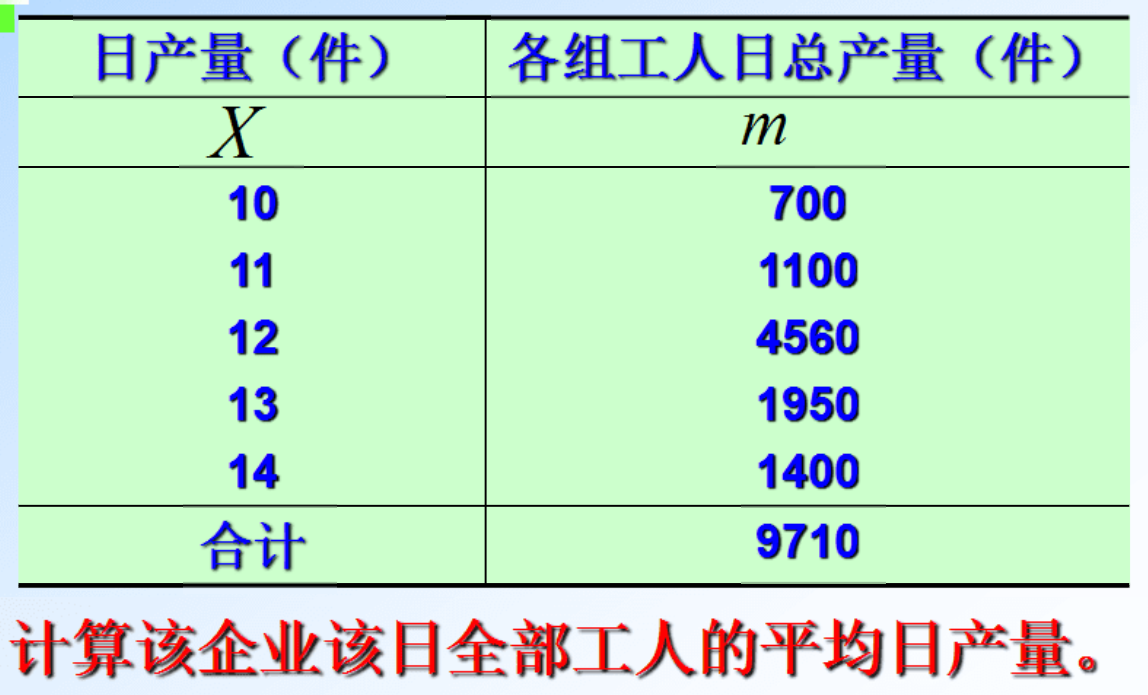

例题2
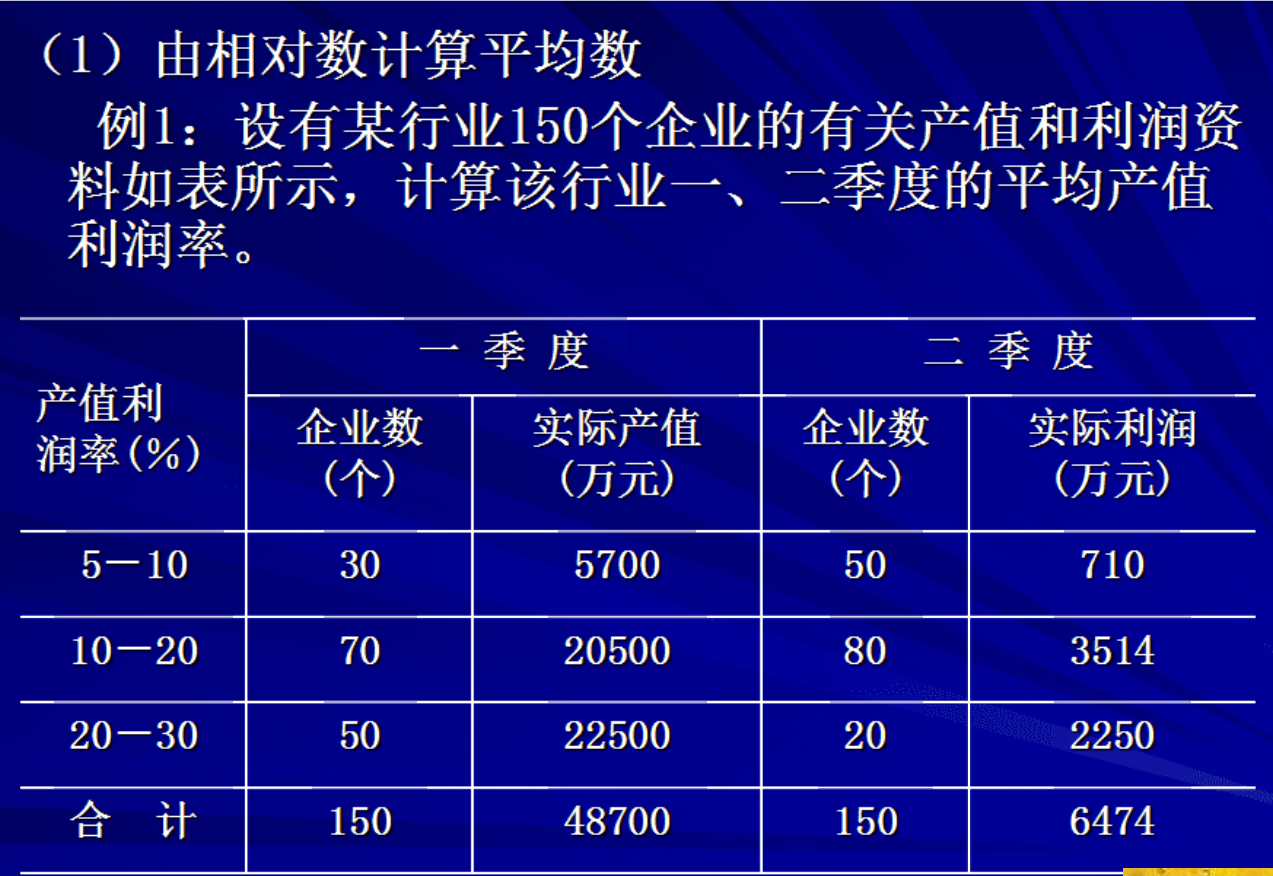

几何平均数
例题1

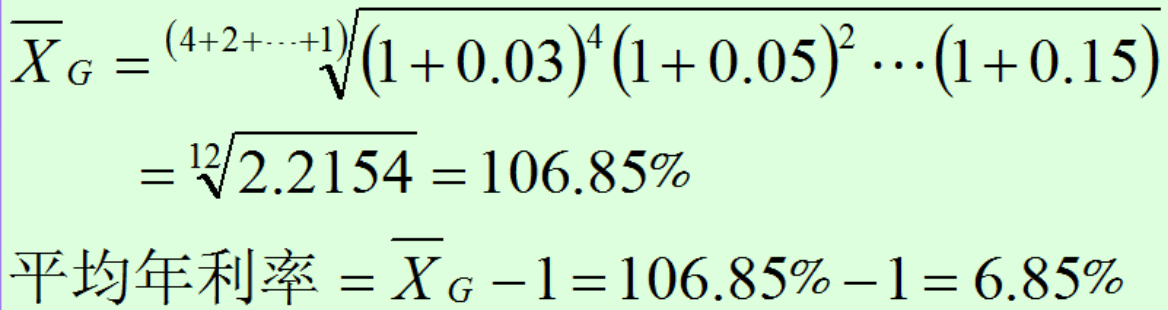
题目中说按照复利,故使用几何平均数。当按照单利计算时,答案如下:
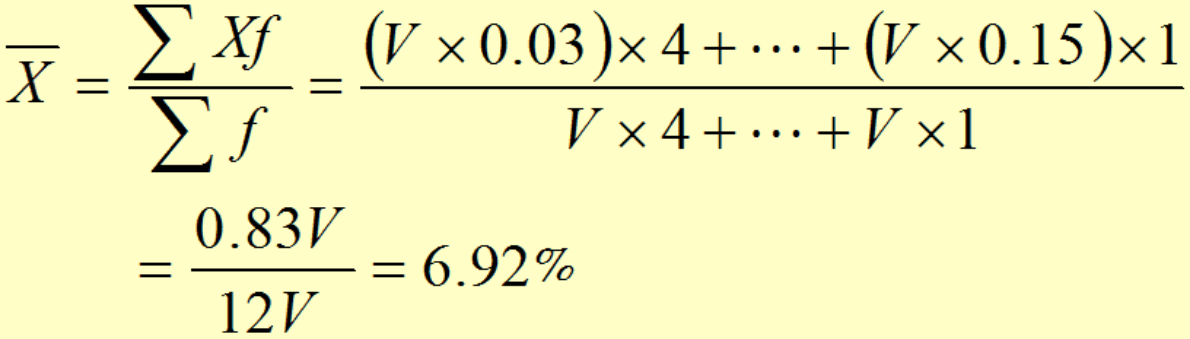
例题2

在组距数列中确定中位数
假定数据均匀分布,直接推导可以得到答案,公式傻长,建议手推,不要背。
在组距数组中确定众数
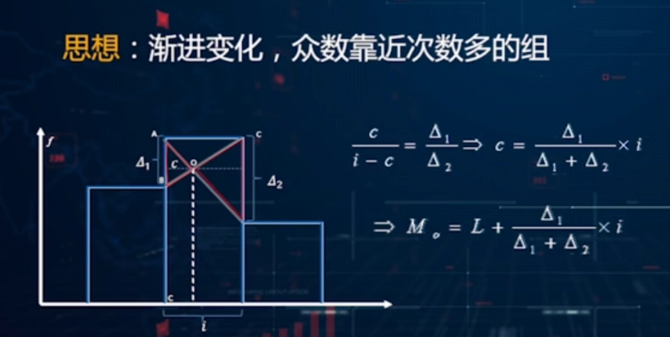
在组距数组中确定四分位数
同中位数的计算.
极差(全距)
最大值-最小值 \(R=Max-Min\)
四分位差(內距)
四分之三分位数-四分之一位数
异众比率
例题
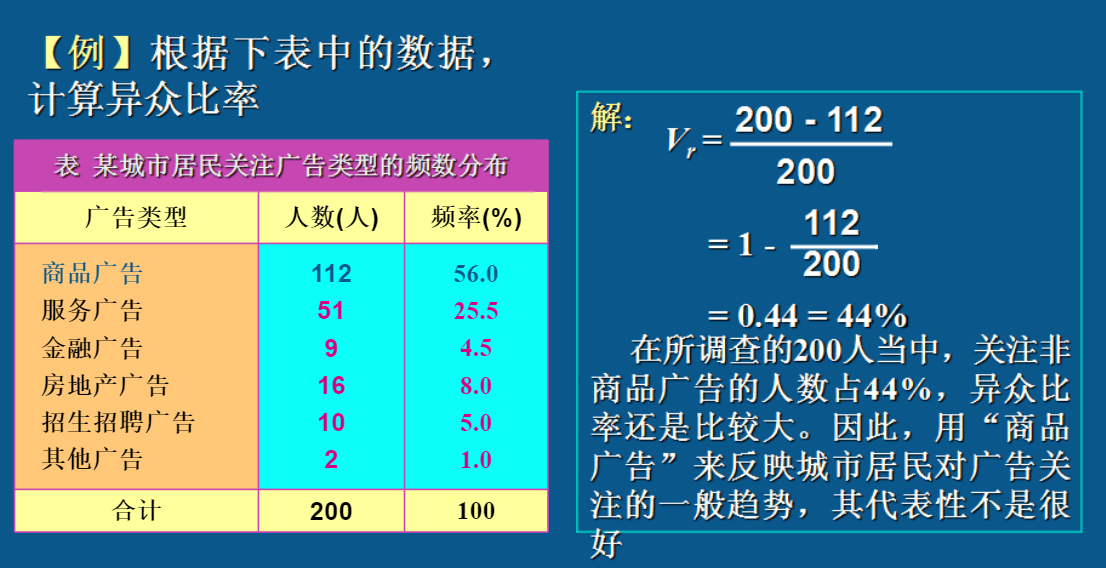
平均差
例题

加权平均差
例题

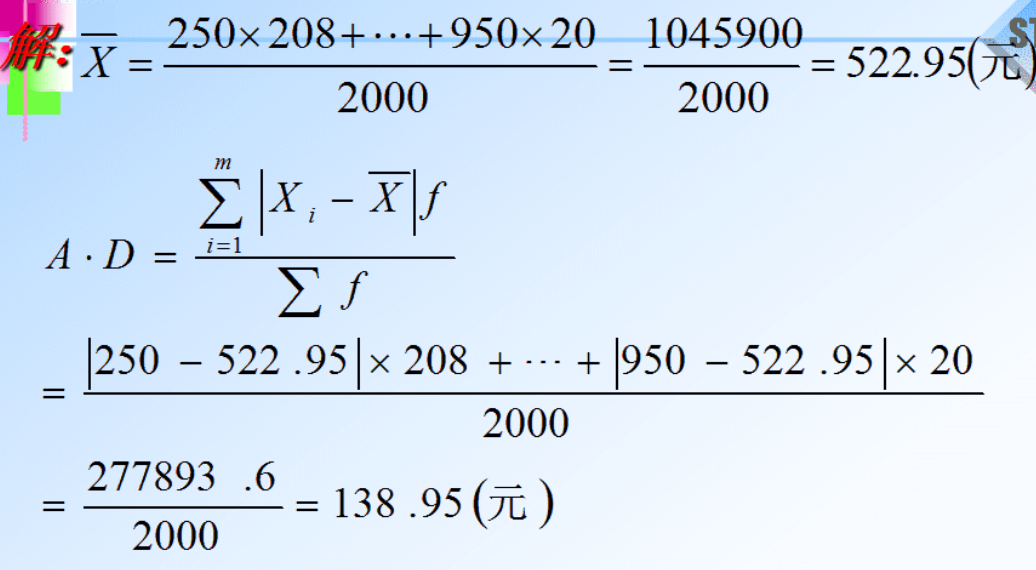
方差
即把平均差的绝对值换成了平方
例题

加权方差
样本方差
把方差的分母多减去一个 \(1\) ,加权样本方差同。
标准差
方差开平方。
离散系数
标准差除以算术平均数
例题
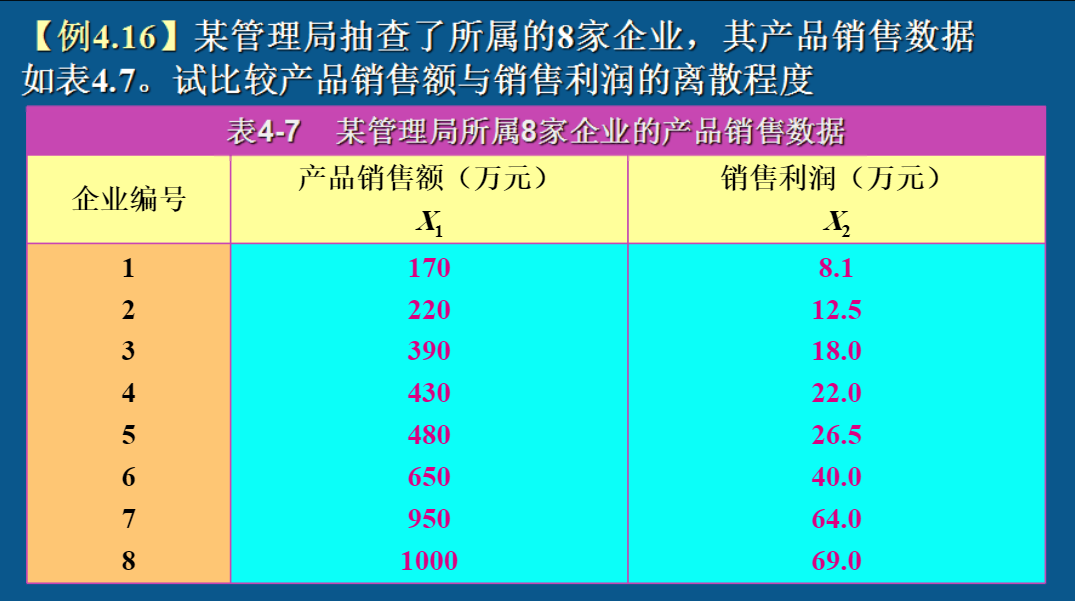
这里只演算产品销售额:首先计算 \(\bar x=536.25\) ,随后计算 \(\sigma =\sqrt{\dfrac{\sum^n_{i=1}(x_i-\bar x)^2}{n-1}} \approx 309.1896\) ,随后计算 \(V_\sigma=\dfrac {\sigma}{\bar x}\approx 0.577\) 。
是非标志
即将普通的 \((x_1,x_2,...,x_N)\) 变为 \((0,1)\) ,公式同上,稍微变换即可。
- 均值:\(\bar x=\dfrac{1*f_1+0*f_2}{n}\)
- 标准差:记 \(P=\dfrac{f_1}{n},Q=\dfrac{f_2}{n}\) ,则可以简化为 \(\sigma=\sqrt{P*Q}\)
- 方差:\(简记为\sigma^2=P*Q\)
标准差系数
例题

样本平均数的抽样标准误差
重复抽样时:\(\mu=\sqrt{\dfrac{\sigma^2}{n}}\) ,不重复抽样时:\(\mu=\sqrt {\dfrac{\sigma^2}{n}(\dfrac{N-n}{N-1})}\) 。
样本成数的抽样标准误差
即在 \(N\) 个样本中随机挑选 \(n\) 个进行抽查——发现合格率是 \(p\) ,则
重复抽样时:\(\mu=\sqrt{\dfrac{p*(1-p)}{n}}\) ,不重复抽样时:\(\mu=\sqrt {\dfrac{p*(1-p)}{n}(\dfrac{N-n}{N-1})}\) 。
抽样极限误差计算
在原来的抽样标准误差的基础上乘以 \(t\) 得到误差 \(\Delta\) 。
样本成数、样本平均数的极限误差:\(\Delta=t*\mu\) 。
置信区间
由上面计算出的误差,可以得到置信区间的范围:
- 总体平均数的置信区间——\(\bar x -\Delta \le \bar X \le \bar x + \Delta\) 。
- 总体成数的置信区间——\(p -\Delta \le P \le p + \Delta\) 。
推测总数平均数需要的样本容量
- 重复抽样—— \(n=\dfrac{t^2\sigma^2}{\Delta^2}=\dfrac{\sigma^2}{\mu^2}\) 。
- 不重复抽样—— \(n=\dfrac{Nt^2\sigma^2}{N\Delta^2+t^2\sigma ^2}=\dfrac{N\sigma ^2}{N\mu ^2+\sigma ^2}\) 。
推测总数成数需要的样本容量
- 重复抽样—— \(n=\dfrac{t^2p(1-p)}{\Delta^2}=\dfrac{p(1-p)}{\mu^2}\) 。
- 不重复抽样—— \(n=\dfrac{Nt^2p(1-p)}{N\Delta^2+t^2p(1-p)}=\dfrac{Np(1-p)}{N\mu ^2+p(1-p)}\) 。
一元线性回归模型
综合总指数公式
\(p\) 表示价格,\(q\) 表示销售量;下标 \(_0\) 表示基期,下标 \(_1\) 表示报告期;\(I\) 表示指数。
加权算术平均指数公式
已知“销售量个体指数”与”基期销售额“:
加权调和平均指数公式
已知”个体价格指数“与”报告期销售额“:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号