学习笔记——刷题小记(1)

前言

$ \tt\huge <本文已完结> $

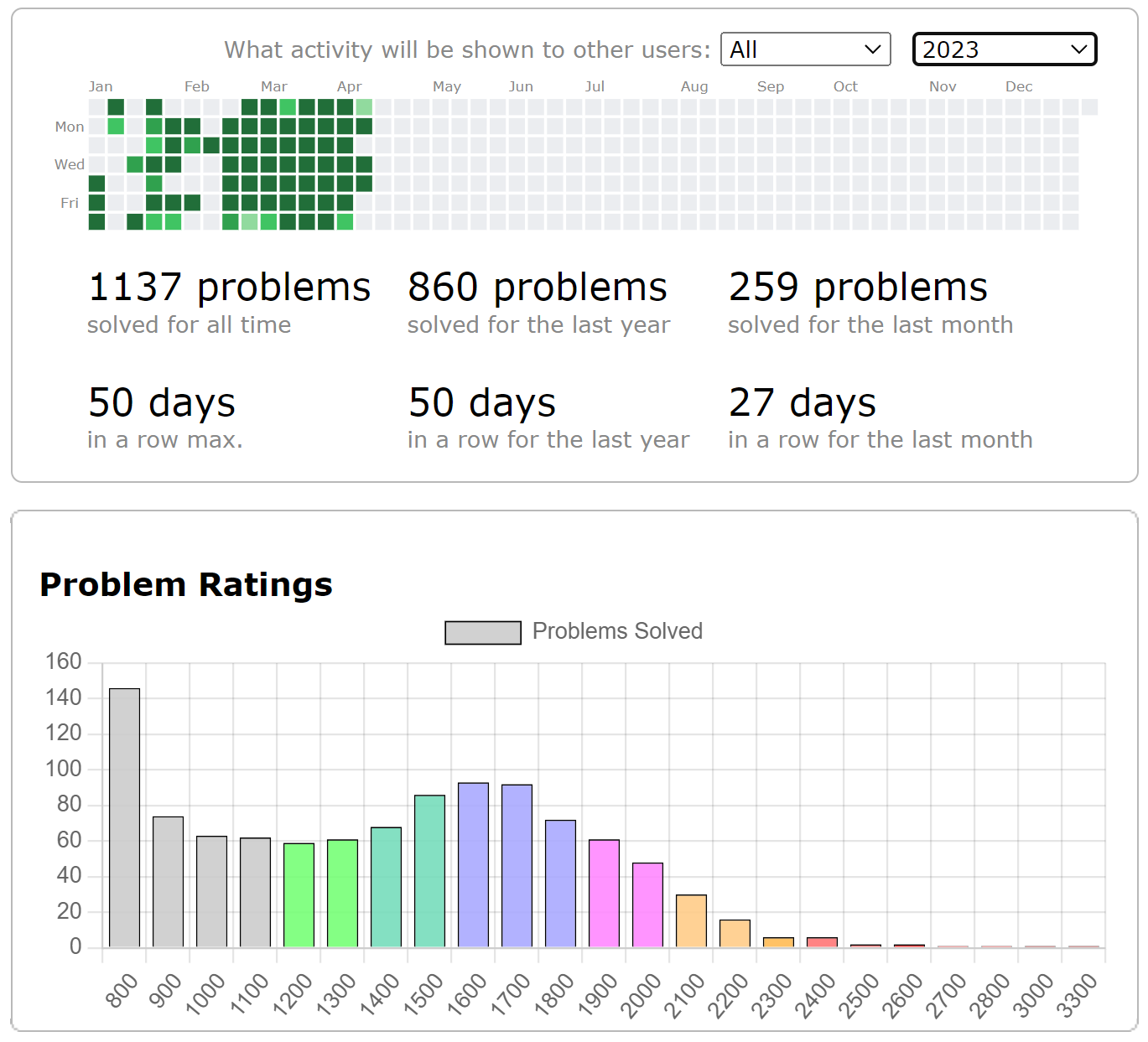
本文自2022.12.13日开始记录，至2023.04.14为止。四个月的时间，我的刷题数从六百题不到一路上涨至1137题，最终在省赛中靠一手运气收获银尾。

$ \tt\huge <故事尚未终结，我们终将继续向前~> $

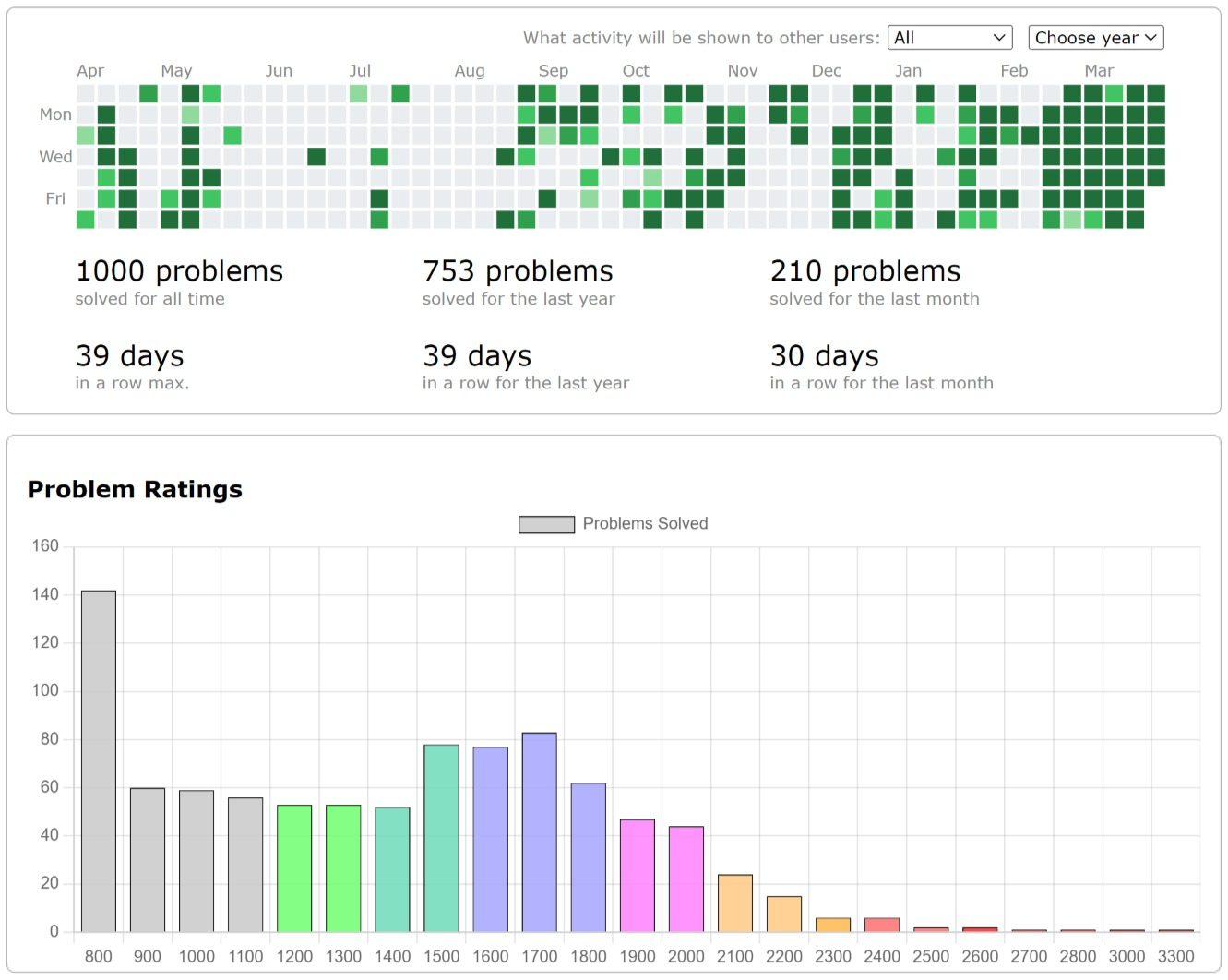
纪念：1000题时刻（2023.03.30）

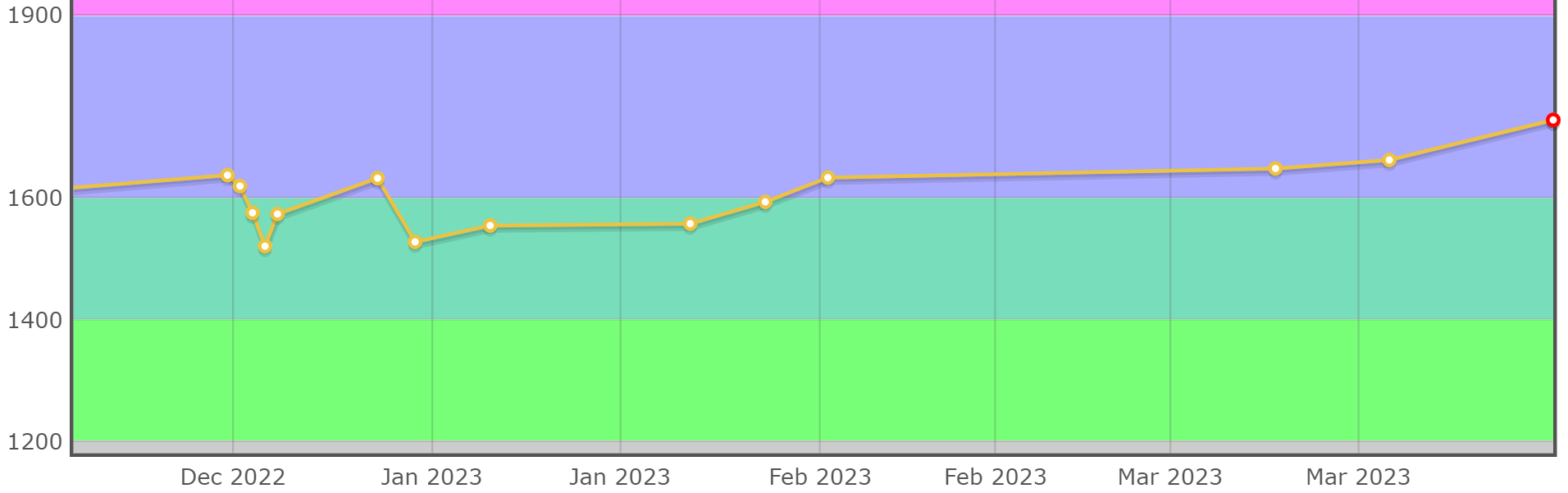
纪念：生涯首次蓝名（2022.12.15）

备注

\(\color{#d0af4c}{\text{#d0af4c}}\) ：模板题。

\(\color{#5c9291}{\text{#5c9291}}\) ：好题。

\(\color{#9d5b8b}{\text{#9d5b8b}}\) ：需要重构。

\(\color{#df0030}{\text{#df0030}}\) ：Wrong Answer。

一些没匹配上具体日期的题目

508D - Tanya and Password

字符串建图后跑欧拉路径。

1721D - Maximum AND

某次比赛中没做出来的题。是一道位运算超级好题！

1554C - Mikasa \(^{*1800\text{；位运算}}\)

巧妙的使用了异或“半加”的性质解题。

1715D - 2+ doors \(^{*1900\text{；位运算+图论}}\)

没有很弄懂的题目。

1538C - Number of Pairs \(^{*1300\text{；二分}}\)

第一遍做被卡死的性质题。

1806E - Tree Master \(^{*2200\text{；暴力+图论}}\)

某次比赛没做出来的题，是欺骗题但是依旧T了，原因在于 \(\tt map\) 中元素塞入过多，补题时发现，只要使用 \(\tt map\) 就会被卡到超时（阴险的hacker），于是引入了类似于莫队分块的思想，使得离散数据能够被暴力计算，聚合数据能够被二维数组记录后多次引用（避免重复计算）。

1270G - Subset with Zero Sum \(^{*2700\text{；图论+构造}}\)

移项后发现是向内基环树，转换成求解环上元素。

741C - Arpa’s overnight party and Mehrdad’s silent entering \(^{*2600\text{；图论+构造}}\)

时间太久远了，忘记转换过程了……转换后即求解二染色。

校赛后~省赛前（仅记录极少部分）

2023.04.13 \(^{30=23+7\text{；什么都刷一些+周三队内赛题目重复提交}}\)

23B - Party \(^{*2100\text{；构造}}\)

离谱题，首先题目意思非常不明白（懂了，锻炼猜题能力），其次，要干什么也非常不明白。不过弄懂了之后还是挺有意思的（构造题都这样）。

一共有 \(n\) 个人开in趴，人与人之间有朋友关系，关系是相互的，关系由你确定。

如果有人的朋友离开了，那么他的朋友数会减少。随后进行操作：没有朋友关系的人全部离开，然后，在剩余的人中仍保持只有 \(1\) 条朋友关系的人离开，以此类推，最后，在剩余的人中仍保持只有 \(n-1\) 条朋友关系的人离开。

请你构造出一种关系网，使得最终剩余的人最多，输出最多的人数。

1810E - Monsters \(^{*2100\text{；图论}}\)

赛时遇到的题目，虽然敏锐的意识到了这是题复杂度欺骗题，但是终剩余一小时也没能搞定掉。

这确实是一题复杂度欺骗题：枚举所有未被遍历过的 \(0\) 点，然后跑 \(\tt bfs\) 即可（细节在于，如果发现以这个点为起点跑 \(\tt bfs\) 无法达成目的，则恢复这一轮遍历中使用到过的 vis 数组）。

随后我们来分析复杂度：记从任意一个 \(0\) 点 \(x\) 出发，能击败的所有怪兽所组成的集合为 \(S(x)\) ；根据上述步骤可以发现，由于我们枚举的是未被遍历过的 \(0\) 点（设其为 \(u\) ），另外有一个已经被遍历过的 \(0\) 点（设其为 \(v\) ），那么一旦 \(u\) 能到达 \(v\) ，就说明至少有一只危险等级 \(\ge |S(v)|+1\) 的怪兽被击败了（换句话说，在击败这一只怪兽前至少已经击败了 \(|S(v)|\) 只怪兽），所以我们有 \(|S(u)| > 2 \cdot |S(v)|\) 。至此，本题大致的复杂度走向为 \(\log\) 级别，总复杂度接近于 \(\mathcal O(N\cdot \log N)\) 。

这一思想（类似于启发式合并）在 \(\tt DSU-on\ tree\) 上也有体现；同时，本题也可以直接使用启发式堆合并、启发式线段树合并等方式解决。

1650B - DIV + MOD \(^{*900\text{；数学}}\)

弱项题，推了好久，赛时遇到直接炸……

2023.04.12 \(^{?\text{；?}}\)

1470A - Strange Birthday Party \(^{*1300\text{；贪心}}\)

贪心好题。

2023.04.10 \(^{?\text{；树上专题}}\)

832D - Misha, Grisha and Underground \(^{*1900\text{；树}}\)

\(\tt LCA\) 好题。如何将所求内容转化为 \(\tt LCA\) 从而规避分类讨论，这是这道题的精髓所在。

2023.04.07 \(^{?\text{；树上专题}}\)

61E - Enemy is weak \(^{*1900\text{；数据结构}}\)

树状数组处理逆序对。在模板的基础上略微变化，单独列出来的原因有二：其一是模板有问题，原来的模板在结构体重定义的时候将 this.n 定义为 n + 1 会导致越界；其二是模板处理重复数据问题，使用 map 单独计算重复数据或者离散化后使用树状数组均可解决，前者略慢一点点（应该出在 \(N\log N\) 的 \(N\) 上，离散化后 \(N\) 比题目中给的更小）。

此前一直不敢深入了解树状数组，以为掌握了线段树就高枕无忧了，随着刷题数的越来越多，越来越意识到这两者还是有各自的独特之处的。狠狠的补习树状数组！

675D - Tree Construction \(^{*1800\text{；数据结构+树}}\)

精彩绝伦的数据结构处理！对于 \(\tt map\) 的理解加深了。

1076E - Vasya and a Tree \(^{*1900\text{；树}}\)

树上差分（没接触过这个算法，姑且这样叫），虽然是区间问题，但是可以用差分巧妙化解，使用线段树等结构也能解题，不过要带修。

2023.04.06 \(^{9\text{；水题乱刷+树上专题}}\)

高强度刷题的第46天，很累，感觉初心不再。答应了个项目，周末去散散心。

620E - New Year Tree \(^{*2100\text{；数据结构+树}}\)

树上线段树处理，比较模板。以前做过但是WA了，这次补题，发现之前WA是因为 bitset 开小了

472D - Design Tutorial: Inverse the Problem \(^{*1900\text{；树}}\)

组合题，暴力建图后跑最小生成树，随后跑两点间最短路验证数据正确性。由于是树上，所以最短路可以直接用 \(\tt dfs\) 做（之前没遇到过），也可以照旧跑 \(\tt djikstra\) ，反正就差了一个 \(\log\) 的复杂度。

提交后发现耗时较长，看了一些别人的代码，发现由于这题庞大的数据输入，使用快读可以提速扎扎实实的一倍，于是收获一个快读板子。

2023.04.05 \(^{?\text{；?}}\)

1671E - Preorder \(^{*2100\text{；分治}}\)

上古时期打比赛没写出来的题。做分治题比较少，感觉相当有趣。

630K - Indivisibility \(^{*1500\text{；容斥}}\)

赛时以为是min25筛之类的高阶做法，但是通过人数非常不对劲。补题时发现，所要求的数字只需要同时满足不被 \(2,3,5,7\) 整除，那么下一步就是计算有多少个数是不满足的。

我们发现，如果直接计算 \(n-\frac{n}{2}-\frac{n}{3}-\frac{n}{5}-\frac{n}{7}\) ，那么 \(2,3\) 的公倍数、\(2,4\) 的公倍数、……均被计算了两遍（多减了一次），于是要加上这些重复的数字，于是式子为 \(n-\frac{n}{2}-\frac{n}{3}-\frac{n}{5}-\frac{n}{7}+\frac{n}{6}+\frac{n}{10}+\frac{n}{14}+\frac{n}{15}+\frac{n}{21}+\frac{n}{35}\) ；那么 \(2,3,5\) 的公倍数、\(2,3,7\) 的公倍数均被计算了两遍（多加了一次），于是要减去这些重复的数字……

最终答案为： \(n+(-\frac{n}{2}-\frac{n}{3}-\frac{n}{5}-\frac{n}{7})+(\frac{n}{6}+\frac{n}{10}+\frac{n}{14}+\frac{n}{15}+\frac{n}{21}+\frac{n}{35})+(-\frac{n}{30}-\frac{n}{42}-\frac{n}{70}-\frac{n}{105})+\frac{n}{210}\) 。

630O - Arrow \(^{*2000\text{；几何}}\)

比较简单的几何模拟题，用到了正弦定律。分数极为虚高。

630P - Area of a Star \(^{*2100\text{；几何}}\)

通过正 \(n\) 边形容易算出圆心角和圆周角（均是两倍的关系），随后用正弦定律算出第二条边，再用余弦定理计算面积即可。

分数极为虚高。

630Q - Pyramids \(^{*1700\text{；几何}}\)

考察了正 \(n\) 棱锥体积公式，不能百度的情况下分数过低，能百度的情况下直接可以秒掉。

棱长为 \(l\) 的正 \(n\) 棱锥体积公式 \(\displaystyle V=\frac{l^3\cdot n}{12\tan \frac{\pi}{n}}\cdot\sqrt{1-\frac{1}{4\cdot \sin^2\frac{\pi}{n}}}\) 。

2023.04.04 \(^{18\text{；组合数专题+VP}}\)

下午刷题看到一场特别的EDU，题目数量很多、难度也不高，于是晚上开启了一场社团内VP挑战。半夜有一场Div3，随便看了看题发现倒数第二题是图论，而且比较一眼的看出是割点问题，于是写了一下，居然A了，可喜可贺可喜可贺（5号补充：然而发现其他人好像都是用并查集做的）。

1444B - Divide and Sum \(^ {*1900\text{；组合数}}\)

没见过的结论。

对于长度为 \(2\cdot N\) 的数列 \(a\) ，将其任意均分为两个长度为 \(N\) 的数列 \(p,q\) ，随后对 \(p\) 非递减排序、对 \(q\) 非递增排序，定义 \(\displaystyle f(p,q)=\sum_{i=1}^{n}|p_i-q_i|\) ，那么答案为 \(a\) 数列前 \(N\) 大的数之和减去前 \(N\) 小的数之和。

327C - Magic Five \(^{*1700\text{；组合数}}\)

题目倒是没有很难，但是我的Zmod模板出现了问题，即对于longlong型的计算非常之不友好（因为原来的板子里 define int 需要关闭，就使得用longlong很麻烦，于是我干脆将Zmod模板修改成了支持longlong输入的形式，从此以后再也不需要关闭 define int 辣！

以前觉得这个修改会很困难，所以迟迟没有进行，这次试验了一下发现还是非常好修改的。

2023.04.03 \(^{14\text{；组合数专题}}\)

1696E - Placing Jinas \(^ {*2000\text{；组合数}}\)

有趣。分析后发现就是一个杨辉三角模型，随后发现暴力会超时，于是化简一维计算。

986B - Petr and Permutations \(^ {*1800\text{；数学}}\)

第一次遇到这种题，纪念一下。首先夸张的数据范围就很有意思，题解区大佬说，只有数据范围很大时才能完全的区分出这中间相差的 \(4\cdot+1\) 次操作（形象的说，一次操作，序列一定更加无序一些，所以可以称之为“无序程度”大到可以区分两个人）

随后，根据性质交换序列的任意两元素，序列的逆序数的奇偶性必定发生改变简单的得到结论。

1545B - AquaMoon and Chess \(^ {*1900\text{；组合数}}\)

感觉很像典啊，把“11”和“1”遇见的情况想象成它们交换了位置，于是所有“1”都可以被忽略，答案只与“11”和“0”的数量有关。

1236B - Alice and the List of Presents \(^ {*1500\text{；组合数}}\)

某类典题，总结不出来，但是看了代码就懂。

2023.04.02 \(^{6\text{；VP摆烂}}\)

凌晨打愚人场，下午VP，晚上聚餐，导致这天没有自己刷题。下午的团队VP还只写了一道题，惭愧。

2023.04.01 \(^{10\text{；*1800乱刷+愚人节专场}}\)

乱刷的题目以模拟为主；愚人节的题目基本也都是抄的，没啥特别大的含金量。

2023.03.31 \(^{11\text{；什么都刷一点+比赛}}\)

晚上的比赛还是非常有意思的，前四题因为样例的强大一次都没有WA，第五题是擅长的图论但是是复杂度欺骗题，虽然有意识到这一点，但是写着写着还是陷入了优化的泥潭，导致最后没写出来。

1466E - Apollo versus Pan \(^ {*1800\text{；进制；数论}}\)

神必进制题。

1285D - Dr. Evil Underscores \(^ {*1900\text{；树；dp}}\)

\(\tt Trie\) 上 \(\tt dp\) 模板题。

2023.03.30 \(^{19\text{；*1800乱刷}}\)

1362C - Johnny and Another Rating Drop \(^ {*1400\text{；数学规律}}\)

神奇规律。

1C - Ancient Berland Circus \(^ {*2100\text{；几何}}\)

写了一晚上……这题很是离谱，大部分解法都没办法严格证明，找了很久才找到一个我自己能够接受证明的。简单介绍如下。

根据给定三点位置，借助海伦公式求得给定三角形面积、借助三角形外接圆公式求得外接圆半径、借助余弦定理（ \(\cos A = \dfrac {b^2+c^2-a^2}{2bc}\) 大部分解法错在这里）求得给定三角形三个角的角度 \(\alpha,\beta,\gamma\) 。

得到上面的全部条件之后，我们发现，最小的多边形的角度 \(=\gcd (\alpha,\beta,\gamma)\) ，进而求得多边形圆心角 \(=2*\gcd\) ，借助三角形面积公式（ \(S=\dfrac{ab\sin C}{2}\) ）求得多边形内单个三角形面积，最终求得多边形面积。

混乱的地方有这样几处：

• 板子中实数域求 \(\gcd\) 的代码判断条件是 1e-5 ，我想当然的将其改为 1e-7 导致错误；
• 圆心角与圆周角弄混了，我一直以为 \(\gcd\) 求得的是圆心角，其实不然；
• 弧度与角度混淆，公式不熟悉。

总体来说，虽然极多的人使用无法证实的结论通过了本题（利用奇怪的公式求得两个角之后，再用 2 * PI 减去这两个角得到第三个角：提问链接），但依旧有完美的过题方法，作为第一场round的压轴题，相当精彩。

1324D - Pair of Topics \(^ {*1400\text{；两点法}}\)

看到这个分数出现在这篇文章里，就知道这题不简单。根据题目所给的式子进行移项（这个好像是典了）后可以发现顺序与答案无关，于是存在单调性，于是可以用两点法/二分之类的做，很简单；如果没有发现顺序与答案的关系，你需要使用权值线段树、cdq分治之类的神必做法来解题。

我就是即没有发现单调性又不会复杂做法的中间层用户。

1450C2 - Errich-Tac-Toe (Hard Version) \(^ {*2300\text{；构造}}\)

复杂度证明题，在C1的基础上容易想到，将 \((i+j)%3\) 的其中两个改成相反的，那么一定是平局的情况，而乍一看这样最多需要修改 \(\dfrac{2K}{3}\) 次，其实不然。容易发现，一定不需要修改的格子数量为 \(\dfrac{K}{3}+1\) ，而由于剩下的格子上 \(XO\) 都有可能出现，\(X\) 出现的多了就将 \(O\) 修改成 \(X\) ；\(O\) 出现的多了就将 \(X\) 修改成 \(O\) ，在数学上这可以被泛泛的用 抽屉原理 解释。

所以，按照上述构造法，最坏需要修改 \(\dfrac{2K}{3}\cdot \dfrac{1}{2}\) 个格子，符合条件。

写的时候 \(K\) 算错了，我是呆呆鸟。

1477A - Nezzar and Board \(^ {*1800\text{；数论}}\)

这道题很棒，详细的记录一下。

假设已知 \(x_1,x_2,x_3,x_4\) ，那么我们如果要计算新的值的话，无非这样几种情况：

• 用本来就已知的值计算，例如：\(a=2x_1-x_2\) ;
• 用刚刚算出来的值计算，例如：\(b=2a-x_3\) ，\(c=2a-b\) 。

无论哪种情况，我们发现，最终都可以化成 \(x=a+(a-b)+(c-x_3)+\dots\) 的形式，在这里，除 \(x\) 外所有的变量都是已知的（包括本来就已知的和刚刚计算出来的值）。

那么，如果 \(k\) 能被表达的话，也符合上式。但是这个式子已知量过多，我们尝试做等价转换，可以得到 \(\displaystyle k=x_1+\sum_{G \in \text{已知变量集合}} (G-x_1)\) 。

不如进一步转化上式，让全部的已知变量都展现出来（通过一个系数处理），如下式：

\[K=x_1+p_1\cdot(x_1-x_1)+p_2\cdot(x_2-x_1)+\dots+p_{|G|}\cdot(x_{|G|-x_1}) \tag{3} \]

当然，直接从 \((1)\) 式转换过来也比较好理解。在这里，\(x_1,x_2,\dots,x_{|G|} \in G\) 。这个方程叫做丢番图方程。

接下来，我们关心这个方程是否有解，这里用到 裴蜀定理 。

裴蜀定理：要使得 \(ax+by=c\) 有非负整数解，那么需要满足 \(ax+by=\gcd(a,b)\) 。

即：要使得 \((3)\) 式有非负整数解，那么需要满足 \(k-x_1=\gcd(x_1-x_1,x_2-x_1,\dots,x_{|G|}-x_1)\) 。至此，本题解决。

1399E2 - Weights Division (hard version) \(^ {*2200\text{；图论；数据结构}}\)

E1的加强版，但是死在了和E1一样的毛病上：比较的时候没有比减半之后最大的值，而是比较了当前最大值。然后改过来了，但是把原来写上去的特判条件漏掉了， Wrong answer on pretest 21 ……

1399E1 - Weights Division (easy version) \(^ {*2000\text{；图论}}\)

第一眼看过去很简单呐，不就一个优先队列处理一下就好了嘛，题解区为什么有人说印象深刻呢，然后就喜提 Wrong answer on pretest 2 了。为什么呢，因为排序的方法搞错了，要将减半之后最大的值放在前，而不是当前最大值放在前面。

1768D - Lucky Permutation \(^ {*1800\text{；dsu}}\)

一月份赛时没做出来的一题，巧妙的将逆序对转换为图上环上问题。现在和那时相比，算法应用熟练了很多，于是没有建图，用了标签里面没有的dsu直接解掉了。（队友hamine居然能在赛时想出来，感觉我好菜）

2023.03.29 \(^{6\text{；*1700乱刷}}\)

本来晚上五点有一场div2的，为了打这场我甚至把课都提前翘了，然而题目毒瘤到爆炸，第一第三题只有概念不同，最后三题只有范围不同，遂放弃。

因为这场div2的缘故，导致白天没怎么刷题（划水Day）。

1141E - Superhero Battle \(^ {*1700\text{；数学}}\)

两个做法，找规律和二分，前者挺思维的（可能是板）、后者需要 __int128 。

1216C - White Sheet \(^ {*1700\text{；几何}}\)

恶心题，模拟了一个小时……

2023.03.28 \(^{9\text{；*1600乱刷}}\)

考虑到省赛的难度，所以今天决定以 *1600 为基准逐渐加难度，晚饭吃完之后就开始 *1800 为基准了，难度和题量都足够。总体来说这一天遇到的题目都不是很难，比较惊艳的应该属于1509C，现在还没搞懂（逃）。

52C - Circular RMQ \(^ {*2200\text{；数据结构}}\)

考察线段树。多了个“环形数组”的特殊条件，但是基本没什么变化。除了读入比较复杂之外，就是模板题了。（然而我 pushdown 的时候最小值忘记处理了，线段树底力还是不够T T）

1354D - Multiset \(^ {*1900\text{；数据结构}}\)

考察树状数组，需要写一个“输出第 \(K\) 大值”的算法，用了二分然后发现被卡时间了，于是学习了一下优化并整合入封装。

同时，本题还可以用权值线段树解，但是我没学过，于是暂时先放放了。

1295D - Same GCDs \(^ {*1800\text{；数论}}\)

没见过的知识点。以下式子成立： \(\gcd (a, m) = \gcd(a+x,m) \Leftrightarrow \gcd(a, m)=\gcd(x,m)\) 。求解上式满足条件的 \(x\) 的数量即为求比 \(\dfrac{m}{\gcd(a,m)}\) 小且与其互质的数的个数，即用欧拉函数求解 \(\varphi \Big(\dfrac{m}{\gcd(a,m)} \Big)\) 。

584D - Dima and Lisa \(^ {*1800\text{；数论}}\)

没见过的知识点。

哥德巴赫猜想：任何一个大于 \(5\) 的整数都可写成三个质数之和；任何一个大于 \(2\) 的偶数都可写成两个素数之和。

素数密度与分布：对于两个素数 \(p_1,p_2 \le 10^9\) ，有 \(|p_1-p_2|<300\) 成立，更具体的说，最大的差值为 \(282\) 。

综上，暴力处理即可。

1509C - The Sports Festival \(^ {*1600\text{；dp}}\)

困惑，不解……

1312D - Count the Arrays \(^ {*1700\text{；组合数学}}\)

漂亮的组合数学板子题。

2023.03.27 \(^{4\text{；*1600乱刷}}\)

满课的周一，本来想晚上回寝室继续刷的，远控忘开了，只能睡觉了。四道题里有三道 \(\tt dp\) ，日常感慨转移方程的巧妙。

1234D - Distinct Characters Queries \(^ {*1600\text{；数据结构}}\)

线段树、树状数组均可做（建立 \(26\) 棵树），然而我拿到题之后的第一反应是莫队，于是打开板子写了个带修莫队上去就过了。也算是复习了下莫队了。

2023.03.26 \(^{1+1+2=4\text{；水题+*1700 dp+省赛团队VP}}\)

周日日常团队VP，所以趁凌晨写了两道题。然而没想到VP打的贼烂，于是这变成了一个划水的周日。

1695C - Zero Path \(^ {*1700\text{；dp}}\)

两种解法，其一是用 \(\tt bitset\) 优化 \(\mathcal O(Nˆ3)\) 的dp，其二是找规律转化。后者可以将问题转化为矩阵最大代价、最低代价dp问题。

然后就在边界没处理这个坑里面了，WA哭了。

2023.03.25 \(^{3\text{；水题}}\)

周六摸鱼日，下午出去玩了，没怎么写题。

2023.03.24 \(^{10\text{；*1600简单数论专刷}}\)

1165D - Almost All Divisors \(^ {*1600\text{;数论}}\)

很好想。

1342C - Yet Another Counting Problem \(^ {*1600\text{;数论}}\)

没见过的知识点。由 \(a\mod b=(b+a)\mod b=(2\cdot b+a)\mod b=\dots=(K\cdot b+a)\mod b\) 可以推广得到 \((a\mod b)\mod c=((K\cdot bc+a)\mod b)\mod c\) ，由此可以得到一个 \(bc\) 的答案周期。

1458A - Row GCD \(^ {*1600\text{;数论}}\)

没见过的知识点。辗转相除法原式为 \(\gcd (x,y)=\gcd (x,y-x)\) ，推广到 \(N\) 项为 \(\gcd(a_1,a_2,\ldots,a_N)=\gcd(a_1,a_2-a_1,\dots,a_N-a_{N-1})\) 。

235A - LCM Challenge \(^ {*1600\text{;数论}}\)

没见过的知识点。连续四个数互质的情况如下，当 \(n\) 为奇数时，\(n,n-1,n-2\) 一定互质；而当 \(n\) 为偶数时，\(\left\{\begin{matrix}n,n-1,n-3 \text{互质}& \gcd(n,n-3)=1\text{时}\\ n-1,n-2,n-3 \text{互质}& \gcd(n,n-3)\neq1\text{时}\end{matrix}\right.\)

1385D - a-Good String \(^ {*1500\text{;分治}}\)

分治板子题，以前好像没写过分治题……

2023.03.22 \(^{\text{队内赛8+水题7+2;*2000分图论Day}}\)

1517G - Starry Night Camping \(^ {*3300\text{;网络流}}\)

看题解水了一题高分题。难点在于找到规律：“题中所述的平行四边形可以转化为网上相邻四个点”，且满足坐标位置关系（这个可能是典），随后建图跑最小割模板即可。

22E - Scheme \(^ {*2300\text{;图论}}\)

之前在Acwing做过一题“添加最少的边使得有向连通图变成SCC”，本题是加强版：图不联通且需要输出一个添边可行解。说实话并不难，只是在前者的基础上增加了一些特判，但是代码长度很夸张整整200行，纪念一下惹。

2023.03.17 \(^{4+4\text{;*2000分图论Day}}\)

1366A - Shovels and Swords \(^ {*1100\text{;思维}}\)

（一看这个tag就知道这题不简单）思维太逊，想不出来，码一下。

999E - Reachability from the Capital \(^ {*2000\text{;图论}}\)

挺喜欢这题的。我们可以缩点，这样形如“首都无法到达 \(x,y\) 城市，但是可以从 \(x\) 到 \(y\) ”这样的城市会变成一个点，非常方便统计；然而，首都能到达的城市也会被缩点的过程处理，所以我们要先增边——使得这些城市成为一整个强连通分量，之后再跑tarjan。

1674G - Remove Directed Edges \(^ {*2000\text{;图论}}\)

同样是很喜欢的一道题，我们发现，题目即为求特殊条件下的最长路。而在这里，因为删除一条边会同时减少一个点的入度和另一个点的出度，所以我们不用思考某条边该不该删除，而是直接判断某个点的入度出度是否均 \(\ge 2\) 即可。这个技巧非常巧妙，但是好像用的非常普遍，狠狠学习了。

557D - Vitaly and Cycle \(^ {*2000\text{;图论}}\)

分类讨论，种类较多。

59E - Shortest Path \(^ {*2000\text{;图论}}\)

输出比较恶心，我用了较多的STL处理边的问题，导致耗时比较长（限制3s我用了1.5s），但是看了一下我的代码应该算是比较好懂的，且可以在细节上优化，所以没有再去优化思路。总体来说，这题属于偏难的题。

2023.03.16 \(^{5+0\text{;高分乱刷Day}}\)

1187E - Tree Painting \(^ {*2100\text{;树;dp}}\)

换根dp模板题，第一次遇到，简单总结下。所谓换根dp题，在不使用dp思想的时候往往是建 \(N\) 棵树（一般仅根节点不同）分别跑暴力，但是由于树的结构不变，所以可以通过dp递推转化。于是，将暴力转化为几遍搜索。

总体来说考验的是dp技巧，切入点一般是子树大小。

438D - The Child and Sequence \(^ {*2300\text{;线段树}}\)

线段树问题，要求将区间值全部取模，这里用到的是数论思维：

• 如果模数大于被模数，就相当于没模；
• 反之，被模数会降至原来的二分之一大小（举几个例子就可以发现）。

讨论的第一条刚好可以用线段树顺手处理一个区间最大值判定；而讨论的第二条是 \(\mathcal O(\log)\) 级别的，所以我们可以直接暴力单点修改。

与之相似的还有对区间开根号，也是 \(\mathcal O(\log)\) 级别的，这都属于比较典的题目。

1225D - Power Products \(^ {*1800\text{;哈希处理}}\)

顺手做的题目。比较取巧，为了储存一个数组，并寻找与其匹配的另一个数组，采用了哈希值+map的做法。

预处理质数和哈希值，随后储存、匹配。总体来说，极其符合这一难度的定义，是我遇到过的较为精准铆定这一级难度的题。

540C - Ice Cave \(^ {*1800 \text{;搜索}}\)

比较简单的搜索，需要一些思维。

1019C - Sergey's problem \(^ {*3000;构造;图论}\)

迷惑题，感觉很好做，恰好与之前遇到过的求点独立集的题目区分开——一遍正向搜索后再用一遍反向搜索检查修正一下即可。

2023.03.15

1365E - Maximum Subsequence Value

有意思的位运算题，赞。

546E - Soldier and Traveling

网络流模板，难点在建图即输出，总体来说比较板。

2023.03.13 \(^{X;\text{构造Day，有部分水题}}\)

1375C - Element Extermination

大量推导构造，最后得出非常简单的结论。

1455B - Jumps

比较搞，看过题解之后还想了很久。

2023.03.12 \(^{1}\)

白天回家补牙，晚上在开组会，基本没怎么刷。

2023.01.11 \(^{1}\)

白天校赛，晚上回家，咕咕。

---

新学期开学后~校赛前的刷题记录（逆序）

2023.03.10 \(^{10;\text{纯水题Day}}\)

1365C - Rotation Matching \(^ {*1400}\)【值得重构】

一开始拿到题完全没思路，看了题解之后发现可以同时记录双方向的操作，随后取众数。其实还是有点不懂。

1365B - Trouble Sort \(^ {*1300}\)

推导之后发现，只要同时存在 \(0\) 和 \(1\) ，那么所有元素均可以进行交换。

2023.03.09 \(^{4;\text{比赛Day，没有额外刷题}}\)

赛时前三题都做得比较顺利，第四题是一道贪心、同时这时群里说第五题比较水，果断跳过第四题做第五题，结果到比赛结束也没写完……最终由于前三题的优势，顺利的恰了一点点烂分。

1802E - Music Festival

其实并不难，推导后发现给定的序列会被处理成递增的。之后题目就变成了暴力，但是需要在较小的复杂度内处理区间最大值的问题。而显然，线段树可以解决这个问题。

提交后发现线段树建树会超时，于是加上了离散化；结果发现还是超时，最后改树状数组通过。

2023.03.08 \(^{7;\text{有部分水题}}\)

82A - Double Cola \(^ {*1100}\)

低分模拟题，对于数字的认知还不够，导致花了好多时间做这题（处理边界问题）。

1472G - Moving to the Capital \(^{*2100;\tt{搜索图论专刷}}\)【值得重构】

有点神奇的 \(\tt dp\) ，非常非常水，感觉分数不超过 \(*1600\) ……

1433G - Reducing Delivery Cost \(^{*2100;\tt{搜索图论专刷}}\)

跑 \(N\) 遍最短路后进行dp（类似于floyd的转移公式），分数虚高。

1796A - Typical Interview Problem \(^{*800;\tt{队内赛}}\)

新生问了问题，一开始没解答出来，以为题目出错了，后来发现是思维没跟上……

不过看榜单有很多大佬也都错在这个地方——即给出的串可能横跨目标串的三个循环节，即 BFBFFBFFBF 这个样例。

1714F - Build a Tree and That Is It \(^{*1900;\tt{队内赛}}\)

构造题，分类讨论六种情况后暴力bfs求解，当然如果数学思维好的话可以规避这个bfs，但是懒得推了。

1748C - Zero-Sum Prefixes \(^{*1600;\tt{队内赛}}\)

逆天贪心+思维题。众数这个性质比较好想，随后是从后往前递推来规避多余的影响。

2023.03.05 \(^{14;\text{有部分水题}}\)

1800A - Is It a Cat?

前一天摆烂没做出来的题目，Div3A，思维题（但是思维烂，WA了3次……）。

1373B - 01 Game（博弈论专刷）

一眼。

276B - Little Girl and Game（博弈论专刷）

发现，能否重新排列为回文串与奇数的字母数目相关，

• 当奇数字母数 \(<2\) 时，先手必胜；
• 否则，双方一定会将字符串取到长度为 \(1\) 为止，判断奇偶即可。

1472D - Even-Odd Game（博弈论专刷）

自己得不到也不能让对手得到，于是一眼看出：排序后从大向小取。

1382B - Sequential Nim（博弈论专刷）

顺序的 \(\tt NIM\) 游戏，我们发现，当某一堆石子数量 \(x_i \ge 2\) 时，先手取 \(x_i-1\) 个石子，后手一定会将这堆石子取光，那么取下一堆石子的时候，先手依旧是先手。

现在的问题在于当某一堆石子数量 \(x_i \le 2\) 的情况。我们发现：

• 如果是中间存在这样的情况（假设场面为 \(…,X,1,1,…\) ）：
  • 有奇数个 \(1\) ，那么先手可以在 \(X\) 那堆直接取走 \(X\) 个石头，这样取完这些 \(1\) 之后先手还是自己；
  • 偶数个 \(1\) ，先手在 \(X\) 那堆取 \(X-1\) 个石子，无影响，先手还是自己。
• 我们可以发现，影响最后结果的，只有前缀 \(1\) 堆的数量。

1365A - Matrix Game（博弈论专刷）

一眼，跟上面那道一眼的题目差不多。

1370C - Number Game（博弈论专刷）

这题目要分类讨论，容易发现，\(n\) 可以拆成 \(2^k*p\) 的形态，对 \(k,p\) 分类讨论即可。比较考研数学思维。

1527B1 - Palindrome Game (easy version)（博弈论专刷）

一眼，后手模仿操作即可。

1527B2 - Palindrome Game (hard version)（博弈论专刷）

其实做上一题时没看到“初始回文”这个条件，直接做成了这一题。首先，初始回文的情况依旧参考上一题；初始不回文的情况需要分类讨论：

• 串为偶数，Bob需要将串变成回文，而Alice只需要等，等到Bob还差一步就达成目的时，掐断他，由自己来达成回文，这样只需要花费 \(1\) ；
• 串为奇数
  • 当 s[n/2] 为 \(1\) 时，当作不存在，同偶数；
  • 当 s[n/2] 为 \(0\) 时，其实也同偶数，但是这个时候双方花费加起来至少为 \(2\) ，由于Alice需要花费 \(1\) ，所以需要额外判定下Bob的花费，可能有平局的情况出现。

总体来说，也不难，细心分类讨论即可。

2023.03.04(0)

讲了一天的课，没做题，摆烂了。

2023.03.03(4)

1198C - Matching vs Independent Set（搜索、图论专刷）

结论题：在一张无向图中，边独立集和点独立集至少存在一个。总体来说不难。

推导：假设边独立集的数量 \(\le n\) ，那么边独立集使用掉的点的数量 \(\le 2\times n\) ，此时未被使用的点的数量 \(\ge n\) ，所有未被使用的点即构成一个点独立集——如果存在两个点 \(x\) 和 \(y\) 不能同时包含于点独立集中，那么一定存在一条边 \((x,y)\) 包含在边独立集中，这导致了矛盾。

1000E - We Need More Bosses（搜索、图论专刷）【无向图割边缩点模板、树的直径模板】

模板题。

1388D - Captain Flint and Treasure（搜索、图论专刷）【值得反复刷的好题】

建图是很显然的，随后我们很容易得到贪心——先行处理正值点。这可以通过一遍 \(\tt dfs\) 完成，还是比较有意思的。

915D - Almost Acyclic Graph（搜索、图论专刷）【值得反复刷的好题】

这道题考察的是 \(\tt topsort\) 的本质，相当的有意思。我们容易发现，暴力删边后重建图跑算法，复杂度为 \(\mathcal O(N\times M)\) ，超时。但是删边后跑 \(\tt topsort\) 的本质实际上是将某一个点的入度 \(-1\) ，那么就不需要枚举边了，直接枚举点就可以了，于是新的复杂度为 \(\mathcal O(N\times M)\) ，可以通过。

2023.03.02(3)

1278D - Segment Tree（搜索、图论专刷）【值得反复刷的好题】

处理 \(N=5\times 10^5\) 范围的线段相交问题，据说是模板，但是我不会，所以就摸了个模板。需要较高的数据结构与 \(\tt STL\) 知识。另外还需要 \(\tt dsu\) 知识作为辅助（判环）。

877D - Olya and Energy Drinks（搜索、图论专刷）

暴力 \(\tt bfs\) 加剪枝，刚开始由于 \(\tt long\ long\) 类型导致超时，再是剪枝失败导致WA，调了好久。过题后想到了另一个剪枝，加上去之后居然变成了 \(\mathcal O(1)\) 的复杂度，算是比较有意思的题目。

842C - Ilya And The Tree（搜索、图论专刷）

基于暴力的树上 \(\tt dfs\) 加遍历。刚开始不会做，去看洛谷题解，一以为这个做法是 \(\mathcal O(N*M)\) 的，果断不看，后来发现另一种基于数论的做法在本质上和这个看似超时的是相通的——由于遍历的是全部的 \(\tt gcd\) 组成的数组，所以复杂度会很玄学，应当是 \(\mathcal O(N*K)\) ，这里的 \(K\) 取决于给定的数据能计算出的全部不同的 \(\tt gcd\) 值。而在 \(\le 2 \times 10^5\) 的值域内任取两个数字得到的不同 \(\tt gcd\) 的数量很小，所以是能通过的。

2023.03.01（5）

1364D - Ehab's Last Corollary（搜索、图论专刷）

很有意思的构造题，最终得到这样的结论：

• 如果没有环（是一棵树），则黑白染色；
• 如果有环，则计算其中一个简单环的大小：
  • 如果这个环的大小 \(\le K\) ，则输出这个简单环；
  • 否则，对这个简单环黑白染色。

在做题的过程中，由于需要找到一个大小 \(\lr K\) 的简单环，我一开始的时候想当然的以为直接找出最小环后加以判定即可，于是我开始写“输出图上最小环的大小”的算法，结果写了几次后发现都无法实现（在重构时我意识到我混淆了简单环和最小环的概念，在查阅知识点后我得知好像没有能在这个数据范围下计算出最小环大小的算法，于是这个想法便是错误的）。

除了上面这个错误之外，我还以为直接将图黑白染色可以替代给环染色，结果很显然——错了。于是，这便是我这道题奇葩错误经历的全过程了。

543B - Destroying Roads（搜索、图论专刷）

多源 \(\tt bfs\) 后暴力枚举，难度不高。

1423B - Valuable Paper（队内赛）【最大流模板】

二分+最大流。*1900的题居然能出网络流的题目，确实有点出乎意料。本题使用匈牙利会超时，同时卡 \(\tt long\ long\) 。

1444A - Division（队内赛）

队内赛题目。比较神秘的数论，我没想的特别明白……

721C - Journey（搜索、图论专刷）

图上 \(\tt dp\) + 路径输出。\(\tt dp\) 带限制，有点类似于背包。

449B - Jzzhu and Cities（搜索、图论专刷）

转化题意后变成最短路计数+最短路判断，有点新颖，但总体来说不是特别难。

2023.02.28

938D - Buy a Ticket（搜索、图论专刷）【“超级源点”模板】

“超级源点”模板题。

796D - Police Stations（搜索、图论专刷）

多源 \(\tt bfs\) ，总体来说不难，因为我个人不是很熟悉这个知识点导致第一遍写的时候写成了顺序 \(\tt bfs\) ，手摸了个样例之后就瞬间明白了。

920E - Connected Components?（搜索、图论专刷）

第二次遇到这样给边的题，这次做能够顺利的处理建图的问题了，然而剩余的问题在于如何基于这个建图方式计算连通块数量。

首先考虑建图，这样的给边方式应当养成习惯。由于给出的是虚假图，容易发现，对于某个点 \(i\) ，其度数越小，在真实图中连接的边的数量就越多。所以，遍历所有点，找到在虚假图中度数最小的那个点，这个点至多连接出去 \(\dfrac{m}{n}\) 条边。于是，通过这个点，我们可以遍历到（真实图中的）至少 \(n-\dfrac{m}{n}\) 个点，所有这些点一定位于同一个连通块内。

此后，对于剩余未遍历过的至多 \(\dfrac{m}{n}\) 个点，暴力枚举全部点，检查哪些点位于同一连通块，这一步的复杂度最差为 \(\mathcal{O} (\dfrac{m}{n}*n)=\mathcal O(m)\) 。

至此，我们发现这样的算法最差的复杂度为 \(\mathcal O(n+m)\) ，过程很暴力，结果非常优秀。

需要注意，本题求解的是连通块，我在书写代码时自作主张，对于已经遍历过的点不再遍历一遍，看起来优化了复杂度，但是导致了答案的错误。

1217D - Coloring Edges（搜索、图论专刷）【 \(\tt dfs\) 树模板】

很优秀的 \(\tt dfs\) 树模板题，当我们找到一个环时，恰好是 \(\tt dfs\) 树中的返祖边。于是，本题即化简为——找出给定图的 \(\tt dfs\) 树的所有的返祖边。

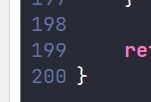
附 \(\tt dfs\) 树模板，虽然已经见过很多次了，但是到应用时还是有点不熟悉：

void dfs(int x) {
	vis[x] = 1;
	for (auto y : ver[x]) {
		if (vis[y] == 0) dfs(y);
		else if (vis[y] == 1) {} // 返祖边
	}
	vis[x] = 2;
}

---

2023.02.27

1343E - Weights Distributing（搜索、图论专刷）

比较好想的 \(\tt bfs\) 题，三遍 \(\tt bfs\) 之后暴力枚举，结合前缀和求解。想方法的时候感觉很复杂（可能是涉及到前缀和我就会感到复杂），但是开始写之后发现思维难度和代码难度都不高。

1176D - Recover it!

显然的贪心，用数据结构之类的模拟一下就行。思维难度低，但是需要有一定的代码水平。

1454E - Number of Simple Paths（搜索、图论专刷）

思维+图论，可能还需要一点点差分的意识。题目给了些隐藏的东西——这张图是一副基环树，以此为突破点加以思考（刚开始没看到这个条件，浪费了很多时间，一定要注意看清图论题的范围）。

1307D - Cow and Fields（搜索、图论专刷）【值得反复刷的好题】

比较有思维含量的题目，首先双源点分别 \(\tt bfs\) 求距离应该很好想，问题在于你只能修改集合中的点，暴力枚举肯定是不行的。最后移项化简后才发现关联之处，思维难度较大，这篇题解写的很明了，可以参考。

1245D - Shichikuji and Power Grid（搜索、图论专刷）

“超级源点”+最小生成树，双模板。

---

2023.02.26

1205B - Shortest Cycle（搜索、图论专刷）

抽屉（鸽巢）原理+无向无权图求最小环。前者不好想（但是题目中所给的范围是强提醒，对于图论手来说看到这样的范围应该要有这样的意识——图论不存在这样的算法求解最小环），后者是板子。

随后出现了本题的另一个巨大黑洞：“或运算”。对于 a[i]==0 的情况，需要进行特判。

1244D - Paint the Tree（搜索、图论专刷）

与其说是图论，不如说是大模拟题，代码巨长（也有可能是我码力太弱）。

容易发现，当且仅当图为单链结构时才有答案，而答案一共只有 \(6\) 种，暴力枚举后判断，随后按顺序输出（而不是按图上序，做题时在这里翻车了）。

242C - King's Path（搜索、图论专刷）

从涂色范围可以发现，直接爆搜即可；从坐标范围可以发现，需要离散化。较水，没多少思维量。

1572A - Book（搜索、图论专刷）

感觉题干在哪里见到过……主要考察了带条件的拓扑排序，稍加修改即可。较水，没多少思维量。

167B - Wizards and Huge Prize（概率期望 \(\tt dp\) 专刷）

最难受的一题，先是没排序卡了一小时，再是下标的问题弄得很混乱，最后排序排错了WA了一次……本题博客链接。

935D - Fafa and Ancient Alphabet（概率期望 \(\tt dp\) 专刷）

分类讨论，难度不大。从前往后遍历，如果前面某一位是需要处理的，

－ 处理为 a[i] > b[i] ：这样处理的话，后面位数就不用管了（除了 a[i] && b[i] && a[i] < b[i] 的情况，所以要单独对这个情况讨论）怎么选都是100%成立，所以直接将这样的概率加入答案即可。
－ 处理为 a[i] == b[i] ：单独计算这样的概率，留作后面再处理。

---

2023.02.25

77B - Falling Anvils（概率期望 \(\tt dp\) 专刷）

几何概型的概率题。这道题需要结合图像、使用面积计算。

根据求根公式，当方程有实根时，\(\Delta = p-4q\ge 0\) 。至此本题转化为 \([0,a]\ge [-4b,4b]\) 的概率，借助图像解：

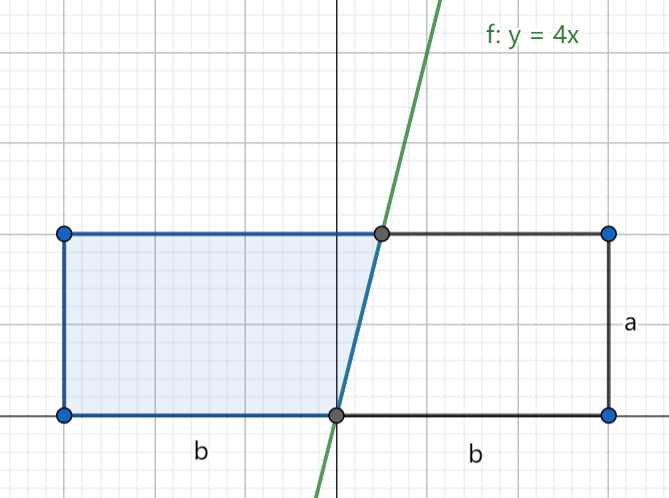
• 当 \(a \le 4b\) 时出现这一情况，此时概率为 \(\displaystyle \frac{ab+\dfrac{a\times a}{8}}{2ab}=\frac{a+8b}{16b}\) 。

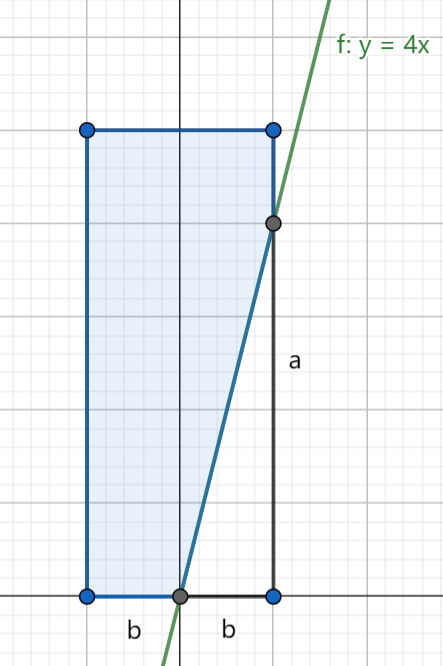
• 当 \(a >4b\) 时出现这种情况，此时概率为 \(\dfrac{a-b}{a}\) 。

• 还需特判 \(a=0,b=0\) 时，概率为 \(1\) 。

• 还需特判 \(a=0\) 时，概率为 \(0.5\) 。

• 还需特判 \(b=0\) 时，概率为 \(1\) 。

442B - Andrey and Problem（概率期望 \(\tt dp\) 专刷）

这道题需要推导公式。

使用 \(dp_i\) 代表到第 \(i\) 个人为止，仅有一人答出的概率；使用 \(lose_i\) 代表到第 \(i\) 个人为止，没有人答出的概率。

那么对于 \(dp_{i+1}\) ，就有 \(dp_{i+1}=dp_{i}\times (1-p_i)+lose_i\times p_i\) ，这个式子可以化简：\(dp_{i+1}=p_i\times (lose_i-dp_i)+dp_i\) 。此时，式子的结果只与 \(p_i\) 的大小相关，故对 p 数组从大到小排序后依次代入求最值即可。

随后可以优化空间，去掉数组。

---

2023.02.24（

626D - Jerry's Protest（概率期望 \(\tt dp\) 专刷）

235B - Let's Play Osu!（概率期望 \(\tt dp\) 专刷）

1753C - Wish I Knew How to Sort（概率期望 \(\tt dp\) 专刷）

540D - Bad Luck Island（概率期望 \(\tt dp\) 专刷）

768D - Jon and Orbs（概率期望 \(\tt dp\) 专刷）

148D - Bag of mice（概率期望 \(\tt dp\) 专刷）

---

2023.01.23

1036C - Classy Numbers

数位 \(\tt dp\) 模板题，但是可以用简单的搜索+数据结构的方法解，又短又好。

1244C - The Football Season

本题博客链接。

1034A - Enlarge GCD

数论+暴力，总体来说并不难想。

463C - Gargari and Bishops

奇怪的题目，感觉考察了构造(?)，主要难点在于寻找一个贪心的方式使得快速求解四方向值之和。

1311D - Three Integers

暴力，确定范围后直接跑嵌套循环。

1388C - Uncle Bogdan and Country Happiness

比较有技术含量的一道树论题，需要有较高的 \(\tt dfs\) 书写技术，变量和细节也都很多。

1400D - Zigzags

标准的 \(\tt dp\) ，挺好想的。

---

2023.02.22

1221D - Make The Fence Great Again

标准的二维 \(\tt dp\) ，不难。

1442A - Extreme Subtraction

抽象后发现是一个前后缀计算题，不难。

1375D - Replace by MEX

分数很高，但是比较简单的构造题。

1381B - Unmerge

很新颖的 \(\tt 0-1\) 背包，抽象出背包问题需要花点心思。

1370D - Odd-Even Subsequence

二分答案，在 judge 函数里需要注意区分奇偶位的计算。

1366D - Two Divisors

利用素数筛计算 lpf ，随后直接判定+输出即可。

1359D - Yet Another Yet Another Task

发现值域非常小，由此作为突破口（尝试将值域引入复杂度）进行暴力枚举。

1369D - TediousLee

超级找规律题，官标 1900 ，然而整体核心代码只有5行，理解起来也不是很难，有点怪……

---

2023.02.21

577B - Modulo Sum

考察了“抽屉原理”：

把多余 \(N\) 个物体放到 \(N\) 个抽屉哩，则至少有一个抽屉里的东西不少于 \(2\) 件。

对应本题，取模后发现当 \(N \ge M\) 时恒成立。

随后，借助变形后的 \(\tt 0-1\) 背包即可解决。

同时，本题可以使用 \(\tt bitset\) 或二进制优化的 \(\tt 0-1\) 背包绕过“抽屉原理”。

1396B - Stoned Game

简单的博弈论，不难想。

467C - George and Job

简单 \(\tt dp\) 题，代码很短。

1359C - Mixing Water

如果直接计算，其实是有点难度的，因为计算一定会涉及到浮点数，而答案是需要输出整数的，所以这里直接分别对浮点数的下取整、整数部分、上取整进行计算，取最优值。

也可以使用二分写。

349B - Color the Fence

初见发现是模拟题（全部数位都一样），后来发现需要借助数据结构进行贪心（数位不一样更优）。总体来说还是简单模拟题。

---

2023.02.20（部分）

2A - Winner

\(\tt map\) 裸题。

371C - Hamburgers

二分答案模板题，细节较多。

448D - Multiplication Table

二分答案模板题，使用哪一个模板需要考虑下（我做这题的时候就卡这里了）。

5C - Longest Regular Bracket Sequence

\(\tt stack\) 解决括号匹配问题模板。

---

以下为寒假初~新学期前的刷题记录，未作整理校对（顺序）

2022.12.25

550D - Regular Bridge

*1900 + 构造 + 图论 。评分虚高，属于比较一眼的题；主要考察构造能力，与图论关联不大，不过涉及到了“割边”的知识，这个图论标签打的没太大毛病。

个人评：*1700甚至更低 + 构造 + 图论 。

1385E - Directing Edges

*2000 + 构造 + 搜索 + 图论 。评分略微虚高，主要需要想到 \(\tt topsort\) ，然后考虑未定方向的边在 \(\tt topsort\) 中扮演一个什么样的角色，只要联想到拓扑序列，问题即被解决了一大半，而后我们能注意到，虽然某条边 \((u,v)\) 未定方向，但是 \(u,v\) 则是拥有拓扑序的，这个拓扑序直接与答案关联。

这道题的构造属性不是特别强，会图论的应该能很快解出。

个人评： *1900 + bfs拓扑排序 + 图论 + 构造 。

1301D - Time to Run

*2000 + 构造 + 图论 + 模拟 。比较典的构造题，评分虚高，原因在于有多种可行的构造方式，区别只在于代码复杂程度；于此同时本题的大致证明会比较显然。但是本题的严格证明可能比较需要技巧，如果将输出长度限制的更极限一些可能才比较适合这道题的评分。

个人评：*1400 + 构造 + 模拟 。写这题的时候参考了一位大佬的代码，在构造思路极为简洁的同时还巧妙的使用函数缩短了代码长度，%%。

542C - Idempotent functions

*2000 + 构造 + 图论 + 数学 。没看太大出来这道题跟构造的关联，主要可能更靠思维，与图论的关联也比较弱（具有图论的性质，但是跟图论的算法无关）。题目非常不友好，看不懂……

个人评：*2000 + 思维 + 数学 。单题博客

2023.01.07

1736D - Equal Binary Subsequences

*2200 + 构造 + 几何 + 贪心 + 模拟 + 字符串 。总的来说不是特别难，偏套路，比较好想，可能有点虚高。虽然有 几何 ，但是没感受到跟几何的关系。

1761E - Make It Connected

*2400 + 二分搜索 + 构造 + 暴力 + DSU + 图论 + 贪心 + 矩阵 + 树 + 两点法 。据说是结论题，但是依照我的水平来说没有任何结论可用，题目较为复杂，需要分五种情况讨论，辅以 \(\tt DSU\) 或其他图论算法。

需要较高的图论技巧，否则即便想到了做法，也难以落实。

个人评：*2400 + DSU + 贪心 + 构造 + 图论 。写这题的时候参考了一位大佬的思路。

1656E - Equal Tree Sums

*2200 + 构造 + 搜索 + 数学 + 树 。发现是结论题！分数虚高很多。

个人评： *1800 + 构造 + 图论 + 搜索 + 树 。本题博客链接 。

1682D - Circular Spanning Tree

*2000 + 构造 + 模拟 + 树 。挺有意思的一道构造题，想到思路不是特别困难，实现起来较有难度，这也或许是题目中这个 模拟 的含义吧。用到了“无向树度之和必为偶数”这一小结论（来判 NO 的情况），不过这个比较好想，稍微推一下就有了。

个人评：*2000 + 构造 + 模拟 + 树 。

1485D - Multiples and Power Differences

*2200 + 构造 + 图论 + 数学规律 + 数论 。这居然是Div2.D，为什么我就没有遇到过这么水的Div2.D……捞的嘛不谈，只能说纯纯脑子题，核心代码不超过十行，这道构造题我只愿意给 *1500 ，不能再多了……如果说限制改为 \(0 \le b_{i, j} \le 10^7\) ，那应该只有 *900 ，即全部输出 \(720720+720720\) ，具体情况可以去看原题，此处不再赘述。

个人评：*1500 + 数学规律 。

2023.01.08

1670E - Hemose on the Tree

*2200 + 位运算 + 构造 + 搜索 + 树 。总体来说是一道相当有意思的构造题，值得这个分数，标签也非常精准。

个人评：*2200 + 位运算 + 构造 + 搜索 + 树 。本题博客链接 。

1278E - Tests for problem D

*2200 + 构造 + 搜索 + 分治 + 树 。这题最大的难点应该在于题目，第一次看错了题，以为要将点转化为二维坐标的点（如图1，点 \(A\) 到 \(E\) 分别代表原点 \(1\) 到 \(6\) ），后来才之后是转化为线段（如图2）。第二次没看到题目中所说的“线段包含”这一条件，导致直接WA1。综合读题难度来说，这道题的给分没有太大毛病。

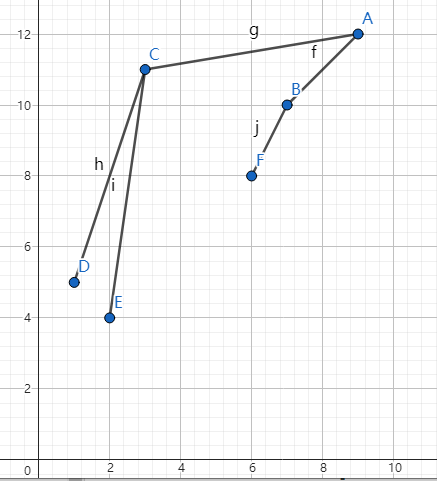
个人评：*2200 + 构造 + 搜索 + 分治 + 树 。

1495C - Garden of the Sun

*2300 + 构造 + 图论 。构造方式并不难想，但是有较多细节，综合来说，评分有点虚高。几乎不涉及图论知识。

个人评：*2000 + 构造 + 图论。

1772D - Absolute Sorting

*1400 + 构造 + 数学 。古早的一场比赛中没做出来的题目，赛时为这道Div3.D编写了百余行的代码，结果WA2，只能说输麻了。补题之后发现这题就考察了个区间取交集，核心代码不超过十行……果然还是太烂了。

2023.01.09

1634E - Fair Share

*2400 + 构造 + 数据结构 + 搜索 + 图匹配 + 图论 。比较精准的标签与评分，本题总体来说并不是特别难，如果能想到图论那么已经解决了一大半了（主要解法是图黑白染色），剩余的难点在于代码的编写，码量题。

对于习惯了ICPC模式的玩家（比如我）来说这题代码的难度反而不大，糅进去的离散化跟没有一样，所以我个人评本题难度会下降一档，属于较为经典的铜牌题（而到不了银牌难度）。

个人评：*2200 + 构造 + 数据结构 + 搜索 + 图匹配 + 图论。

2023.01.10 - 2023.01.20

出去旅游，鸽了。

2023.01.21

484A - Bits

*1700 + 构造 + 位运算 。非常考验位运算思维的一题，不难，熟悉位运算的同学应该能飞速切掉这题。分数比较虚高。

个人评：*1400 + 位运算 + 构造。

493D - Vasya and Chess

*1700 + 构造 + 博弈 + 数学规律 。博弈论基础题，主要考察镜像局面，稍微手玩下就能得出结论。分数比较虚高。

个人评：*1400 + 博弈 + 构造。

1469D - Ceil Divisions

*1700 + 构造 + 暴力 + 数论 + 数学规律 。有一定难度，如果没有 n+8 次的限制就是秒杀题，但是加上这个限制之后则需要进行优化：前者的操作次数很显然是 \(\mathcal O(N^-+\log_2 N)\) （这里 \(N^-\) 代表略小于 \(N\) ），后者则需要在 \(\log_2 N\) 上做文章，使之变成 \(\log_2 \sqrt N)\) 。

个人评：*1700 + 构造 + 暴力 + 数论 + 数学规律 。

1699C - The Third Problem

*1700 + 构造 + 组合数 + 数学规律 。说是构造题，其实更偏向于找规律，从 \(0\) 开始，寻找每个数字可以放置的位置，最后发现其实与区间相关。

个人评：*1600 + 构造 + 数学规律 。

1538D - Another Problem About Dividing Numbers

*1700 + 构造 + 数论 + 数学规律 。这道题的规律对于我个人而言比较一眼，很自然的能和筛联系起来，而后简单判断即可。筛板子题，分数比较虚高。

个人评：*1400 + 构造 + 数论 + 数学规律 。

1360F - Spy-string

*1700 + 位运算 + 暴力 + 构造 + DP + 哈希 + 字符串 。虽然标签众多，但是核心思路就是暴力枚举加判断，本质上就是个无脑暴力题。当然也可以用DP的思想加上位运算优化；在判断的时候可以用哈希的思想。但这些都是添头，本质上还是道简单题。

个人评：*1500 + 构造 + 暴力 + 字符串 。

2023.01.22

1474C - Array Destruction

*1700 + 暴力 + 构造 + 数据结构 + 贪心 + 模拟 + 排序 。数据结构好题，基于暴力进行模拟，利用 multiset 可以极大的简化代码。思维量不大，但是总体码量较大，甚至感觉有点虚低。

个人评：*1700 + 构暴力 + 构造 + 数据结构 + 贪心 + 模拟 。

1268A - Long Beautiful Integer

*1700 + 构造 + 贪心 + 模拟 + 字符串 。题目不难，这里不多描述。但是这道题我第一遍的代码错了两个地方，值得警醒，其一是WA7，原因在比较两个字符串大小时，我直接按位比较，只要 \(s\) 有一位比 \(S\) 大就判定 \(s>S\) ，找到错误后才发现非常弱智，但是在写代码的过程中没发现这个问题（加上小于号的比较可以修正这一问题）；其二是WA40，原因是我的思路是对整个串逆序处理，这就会导致后处理的内容无法反映到已经处理好的内容上去，如 192 这个例子，当循环节为 \(2\) 时我向第一位进位，相对应的第三位也需要改变，但是我的做法未能处理这样的情况（再加一遍判定修改可以解决这一问题，但是代码太长了）。

最终通过重构代码通过了本题，且非常简洁。由于不明白为什么错了这么多次，所以进行了多轮测试，最终得到了上文结论。

个人评：*1700 + 构造 + 贪心 + 模拟 + 字符串 。这道题错了太多次了，对于难度的评价可能不是最公正。

1361A - Johnny and Contribution

*1700 + 构造 + 图论 + 贪心 + 排序 。图论基础题，主要考察 dfs ，想到了就很板。

个人评：*1500 + 构造 + 图论 + 贪心 。

1131F - Asya And Kittens

*1700 + 构造 + DSU 。dsu 启发式合并板子题，将点秩小的（题目中具体表现为连通块小的）合并到点秩大的上面去，然而要想到 dsu 并不容易，我一开始以为是直接建图后 dfs ，测试样例时发现这样做不对，样例还是非常给力的。

个人评：*1600 + 构造 + DSU 。

1227C - Messy

*1700 + 构造 。纯模拟题，很好想，但是代码挺长，除了模拟之外好像啥都没考……不过就模拟的难度来说配得上这个分数。

个人评：*1700 + 构造 + 模拟 。

1148C - Crazy Diamond

*1700 + 构造 + 排序 。破防题，写了接近一个小时，倒不是方法难想（题目给的构造条件很宽松，非常容易构造），而是数组太绕了+需要分类讨论，需要处理原数组和位置数组的交换，很典，但是我不会。作为一道折磨人模拟题，配得上这个分数。

个人评：*1800 + 构造 + 排序 + 模拟 。我对于这种双数组排列的题目接受程度较差，对于难度的评价可能偏高。

2023.01.23

33B - String Problem

*1800 + 最短路 。较为典型的 Flody 题，最近用的比较少，导致我循环条件写错了，错了好几次……建图比较显然。

个人评：*1800 + 最短路 。

1272E - Nearest Opposite Parity

*1900 + 最短路 + 图论 + 搜索 。建图非常显然，随后就是跑最短路的问题，这里有两大类做法，其一是 \(\tt 01\ bfs\) ，其二是建立虚拟源点后跑最短路。注意，由于题目性质，需要建反图。确实有一定难度，但是官方评分可能有点过高。

个人评：*1800 + 最短路 + 图论 + 搜索 。

2023.01.24

1320B - Navigation System

*1700 + 最短路 + 图论 + 搜索 。题目需要求上下限，所以需要进行一定的讨论，第一次做的时候看错题了，导致一直WA7。本题需要分别建立正反图，在反图上跑最短路，在正图上分类讨论，个人感觉难度较高。

个人评：*1900 + 最短路 + 图论 + 搜索 。

2023.01.25

585B - Phillip and Trains

*1700 + 最短路 + 图论 + 搜索 。可以使用暴力搜索，也可以建图后使用 \(\tt 01\ bfs\) 计算。个人偏向于暴力搜索，能不建图就不建图了，总体难度不高。

个人评：*1700 + 搜索 。

1081D - Maximum Distance

见博客

173B - Chamber of Secrets

*1800 + 最短路 + 搜索 。需要一定建图技巧：一个施了魔法的柱子可以将光改变方向，可以看作是将行与列连接，且边权为 \(1\)，未施魔法的柱子会让光线直接穿透，所以可以看作是空白格。之后在建立的图上跑 \(\tt 01\ bfs\) 即可。

个人评：*1800 + 最短路 + 图论 + 搜索 。建图技巧较为套路。

1505D - Xenolith? Hippodrome?

愚人节场的题目，纯愚人，没必要懂为什么。

1505E - Cakewalk

愚人节场的题目，主要灵感来自题意“可能导致她做出次优的决定”，观察样例后发现老鼠路径遵循局部最优原则：总是前往离她最近的那个奶酪。故暴力枚举每一个奶酪距当前格的曼哈顿距离即可。这里出现 special judge 的点，即当有多个奶酪距当前格距离相等时该如何抉择，答案是均可，如下例，输出 \(1\) 和 \(4\) 均视为正确。

5 5
..*..
.....
**...
**...
**...

同时，本题还有另一个 special judge 可以通过的思路（参考自T宝的代码），即：设当前位于 \((x,y)\) ，当且仅当 \((x+1,y)\) 有奶酪、或已经到地图右边界时才向下走，否则均向右走。或反过来：设当前位于 \((x,y)\) ，当且仅当 \((x,y+1)\) 有奶酪、或已经到地图下边界时才向右走，否则均向下走。也能通过该题，如下例，答案可以为 \(0\) 或 \(1\) 。

5 5
.....
.....
*....
.....
.....

2023.01.31

189A - Cut Ribbon

背包——完全背包板题。

455A - Boredom

一道比较简单的 \(\tt DP\) 题，考验基本 \(\tt DP\) 思维。

313A - Ilya and Bank Account

可以用来练习一些函数，如：\(\tt stoi\)，\(\tt substr\)，\(\tt to\_string\) 。

579A - Raising Bacteria

可以用来练习 \(\tt bitset\) 。

1475A - Odd Divisor

可以用来练习时间复杂度的计算（欺骗题）。

2023.01.31

279B - Books

可以用来练习队列，和单调队列思想类似，但不单调。

368B - Sereja and Suffixes

\(\tt set\) 裸题。

519B - A and B and Compilation Errors

数据结构题，多种解法。

2023.02.03

556A - Case of the Zeros and Ones

\(\tt stack\) 裸题，但是可以用贪心解。

1520D - Same Differences

\(\tt map\) 裸题，但是可以用下标增益法规避。

467B - Fedor and New Game

\(\tt bitset\) 裸题。

2023.02.06

698A - Vacations

优秀的 \(\tt dp\) 板子题。

1526B - I Hate 1111

考察了“麦乐鸡定理”；同时，利用数论知识也能通过本题。附使用“麦乐鸡定理”通过本题的代码：

bool Solve() {
	int n; cin >> n;
	for (int i = 0; i < 100; ++ i) {
		for (int j = 0; j < 10; ++ j) {
			if (i * 11 + j * 111 == n) return 1;
		}
	}
	return (n > 1099) ? 1 : 0;
}

2023.02.07

339D - Xenia and Bit Operations

线段树基础题，需要根据题意修改上传更新函数。

2023.02.14

1324F - Maximum White Subtree

树形 \(\tt DP\) 好题，需要进行两遍，一遍自顶而下，一遍自下而上，其中第二遍比较难理解，这篇博客写的非常简洁，很好懂第二遍为什么这样写。

2023.02.15 - 2023.02.19

期末考试

以下为“超级刷的完”计划初~寒假前的刷题记录（顺序）

一些感悟

*1500基本就考察一些图论的基础知识以及基础的 \(\tt dfs、bfs\) ，完全不涉及图上算法。

*1600开始出现图上算法，但都是模板题。

---

好题记录

1472C - Long Jumps

982C - Cut 'em all!

1552B - Running for Gold

挺“有趣”的一道题

1169B - Pairs

想了很久，还算有趣

1511D - Min Cost String

奇妙的构造，这题是一定要研究一下写博客的

1615C - Menorah

毒瘤……第一次见识毒瘤题。但是好像有更优的做法，要补题。

1530D - Secret Santa

这道题给人的感觉就是二分图匹配，而实际上也确实用到了类似的思想，只不过这个更加暴力和贪心。对于二者的区别，我想有必要找个时间详细的比较比较，现在的我好像还没办法清楚的分辨。

同时，由于涉及到“X给Y”和“Y被X给”的关系，所以这道题的计算和输出会用到数组套数组，对于我而言这更加迷糊，是发现WA1之后才加的数组套数组，然后稀里糊涂就过题了。

要补题，同时需要补一补二分图。

763A - Timofey and a tree

两种做法，想了一个晚上结果都被卡了。但是总体来说这道题不难，被卡也是因为看了题解但是没有看的很仔细想当然的顺着题解思路做了，结果理解的是错的。这篇博客很好的写了这道题：https://blog.csdn.net/qq_41289920/article/details/82584642

1418C - Mortal Kombat Tower

DP裸题

510C - Fox And Names

拓扑排序，写了一个小时，挺有新意的（对于我而言）

牛客44749D【试区分：615B - Longtail Hedgehog】

本来感觉这是道简单的最短路变式的图论题，刚开始直接打开了dji的板子也相当的正确，后来写着写着就写偏了，写成了用 vis 数组统计这个点是否被遍历过，严格按照每个点只遍历一次来做，实际上这样是错误的，因为 \(\tt bfs\) 搜索到某个点的路线是最近的，但是答案不一定是最小的，而后续如果某个点的值发生了变化，要重新去更新这个点的邻点，所以应该使用 if 语句检查这个点是否要被改变。

提供一组hack数据。

5 6 1
1 5 1
1 2 2
2 3 2
3 4 2
4 5 2
5 4 1

770C - Online Courses In BSU

好题，独特的 \(\tt dfs\) 思路，有新意。

114B - PFAST Inc.

考察到了之前感到很神奇的枚举子集的方法，除此之外好像有更优的方法，待补。

1437D - Minimal Height Tree

非常优秀的模拟题，很享受。

639B - Bear and Forgotten Tree 3

一道挺有意思的构造题，长得就很像打卡题，有一点思维难度但不完全有。

369C - Valera and Elections

图论，但是 \(\tt dfs\) 里面加东西。

986A - Fair

阴间搜索题，全是数组，绕晕了。

793B - Igor and his way to work

阴间搜索题，看似没毛病的写法很容易就超时了，需要大力优化，但是这个优化并不是很好想，建议补一下，还是挺搞的。

295B - Greg and Graph

\(\tt Flody\) 绝对的好题，考察了这个算法的核心。

1406C - Link Cut Centroids

树的重心好题，考察了这个定义的一些概念与性质。

1242B - 0-1 MST

\(\tt dsu\) 好题，暂时还没想明白为什么合并时不加 ”将编号大的合并到小的上“ 这个优化会导致超时，问了黄文豪但是他好像也没搞明白，需要补题。

1764B - Doremy's Perfect Math Class

有点意思的题，不是很懂，要补补。

---

一句话评

930A - Peculiar apple-tree

小心读题，很难懂

320B - Ping-Pong (Easy Version)

单向/双向边

1139C - Edgy Trees

注意模数

350B - Resort

要反向建图，刚开始做的时候没意识到……

不能直接把答案序列塞到递归里面去，不然会MLE，只能开两个全局变量然后动态维护了（回溯什么的）

177C1 - Party

DSU典题

1106D - Lunar New Year and a Wander

颜面扫地题……这是一道典的不能再典的 \(\tt bfs\) 题，然而我第一把 \(n,m\) 搞反了，第二题目没读懂写成了 \(\tt dfs\) ……

300B - Coach

并查集偏向板子的一道题，题目不是很好读，导致错了好几次，且讨论时比较容易遗漏情况。码量较大。

402C - Searching for Graph

图论+构造。感觉像800分水题，没明白考察了什么。

601A - The Two Routes

最短路板子题，难点在于能不能考虑到给出的图是完全图，以此解决“同一时刻两种路线不能相交”这个问题。

723D - Lakes in Berland

颜面扫地题……一道普通的 \(\tt dfs\) ，稍有难度但理应快速解决，可是因为搜索写炸了+题目没读懂，面向样例编程还错了三次……

659E - New Reform

\(\tt dsu\) 典题，虚高。

731C - Socks

挺有趣的一道数据结构+\(\tt dsu\) 题，小小的思维难度。

1609D - Social Network

中等难度的 \(\tt dsu\) 题，题干超级超级难读，稍有不慎就假了……（威廉王子，看来是英国佬出的题，塞满华丽复杂的语句，不愧是英国佬）

1365D - Solve The Maze

中规中矩的搜索题，可以用来做数据结构的板子题，没有数据结构做这道题代码会长很多。

427C - Checkposts

\(\tt Tarjan\) 处理 \(\tt SCC\) 板子题，不知道为啥第一次写的时候直接写了个 \(\tt Topsort\) 来处理 \(\tt SCC\) ，不过也挺惊人，*1700的题居然就已经出现 \(\tt Tarjan\) 算法了，是我见解不够了。

1253D - Harmonious Graph

\(\tt DSU\) 加上一个”编号小的合并到编号大的上面去“的限定。

1144F - Graph Without Long Directed Paths

染色法判定二分图板子。

1176E - Cover it!

利用图的（生成树的）深度进行贪心计算的问题，非常虚高。

598D - Igor In the Museum

搜索+记忆化，题目看懂了（特别是样例二）就不难，小小虚高。

1383A - String Transformation 1

\(\tt dsu\) 板子题，但是怎么想到 \(\tt dsu\) 可能有点难度，小小虚高。

1068C - Colored Rooks

符合 \(\tt *1700\) 难度的构造题，需要思维，不难。

22C - System Administrator

题目标签不对，这题应该是构造算法为主，与上一题相较感觉难度低一些，思维难度低很多，虚高了。

769C - Cycle In Maze

挺有意思的一道题，主要考察搜索，一贯的，只要涉及了搜索的题目就比较麻烦，这题也是。思维难度较高，有点虚低。

1063B - Labyrinth

题目标签不对，应该再加上一个搜索的标签的。本题可以转化为 \(0-1\) 最短路问题，比较新颖，但是不难。符合这个难度的定位。

1076D - Edge Deletion

\(\tt djikstra\) 略微变形，总体来说不难，除此之外更普遍的解法是”最短路树“，可以去 洛谷题解区找链接 。

118E - Bertown roads

使用 \(\tt Tarjan\) 处理割边，偏向于板子题。