Codeforces - 1740E - Hanging Hearts（图论 + 动态规划、*1800）
1740E - Hanging Hearts（⇔源地址）
tag
⇔图论、⇔动态规划、⇔*1800。
题意
给出一棵 \(N\) 个点的树，现在你需要给树上的每一个点赋值，要求：
- 各个点的值均不相同；
- 值的范围是 \(1-N\) 。
随后，你需要在这棵赋过值的树上进行操作，如下：
- 选择当前的任意一个叶子节点，将其删去；
- 对于上一步删掉的叶子节点的值 \(w_i\) ，如果其父节点的值 \(w_{fa}\) 满足 \(w_{fa}<w_i\) ，则 \(w_{fa}\) 变为 \(w_i\) ；
- 将 \(w_i\) 记录到序列 \(s\) 中去。
要求：寻找某一种赋值方式，使得最终构成的序列 \(s\) 中拥有最长的非递减序列，直接输出这个最长的非递减序列的长度。
思路
容易得到的一些事情：
- 为了得到最长的非递减序列，一定会给深度深的点赋小的值，这样删掉这些点时，这些小的值会一路上传给他们的父节点，如下图所示：
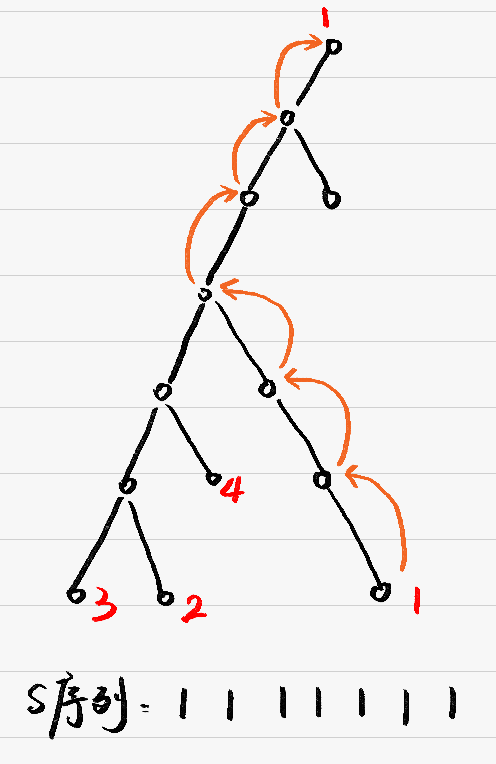
- 对于一个非叶子节点，还有一种贪心的方式是将其能直接到达的每一个叶子节点赋一个值，然后按一枝一枝这样的方式删点，如下图所示：
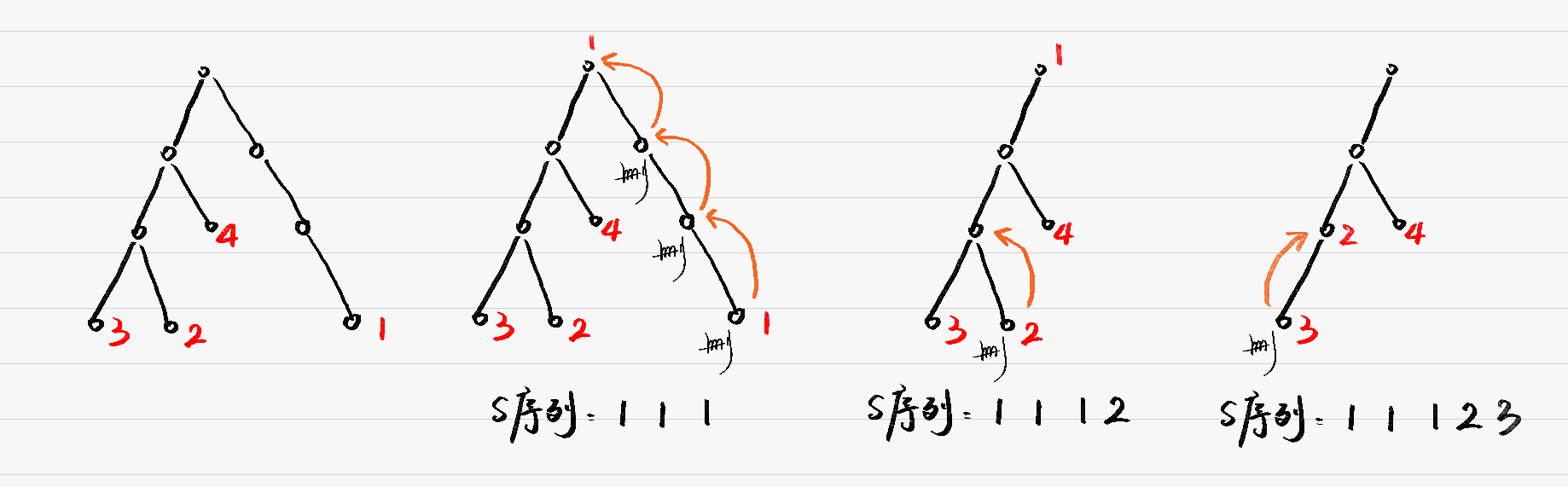
而这就构成了我们这道题解题的关键，讨论哪个方法更优是没有必要的，因为在不同的构造中这两个方法都各有优劣（赛时我一直在思考哪个方法更好，导致没能解出来），所以我们直接使用动态规划解决本题。
对于方法1，我们发现，当前点答案即为到最远叶子节点的距离；而对于方法2，我们可以类比于子树大小，只需要将当前点的全部子节点的值加起来即可。对于上面两个答案，取较大值即为当前点的最终答案。
AC代码
点击查看代码
namespace G {
vector<int> ver[N];
int deg[N], ans[N], dep[N];
/*答案由两种可能构成：
其一是不选择这个点，而是选择其全部子节点的答案之和
其二是选择这个点，那么这个点之前全部选择的点将成为一条长链*/
void add(int x, int y) {
ver[x].push_back(y);
++ deg[y];
}
void dfs(int x, int fa) {
int siz = 0;
dep[x] = 1;
for (auto y : ver[x]) {
if (y == fa) continue;
dfs(y, x);
siz += ans[y];
dep[x] = max(dep[x], dep[y] + 1);
}
ans[x] = max(siz, dep[x]);
}
}
signed main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n; cin >> n;
for (int i = 2; i <= n; ++ i) {
int x; cin >> x;
G::add(x, i);
}
G::dfs(1, -1);
cout << G::ans[1];
return 0;
}
错误次数：1
文 / WIDA
2022.11.07 成文
首发于WIDA个人博客，仅供学习讨论
