【施工中,已完成D、I、M】2020 ICPC 上海(TeamVP)
比赛相关信息
比赛信息
比赛名称: 第 45 届国际大学生程序设计竞赛(ICPC)亚洲区域赛(上海)
比赛地址: Gym补题,牛客补题全部参赛队伍: 632有效队,42打星队
金: Rk 35,7题,1061m
银: Rk 105,5题,916m
铜: Rk 210,4题,732m其他参考:
7题尾: Rk 46
6题尾: Rk 70
5题尾: Rk 111
4题尾: Rk 229
以上数据参考自官方获奖名单,可能与公共榜单有所差别。
比赛过程回顾
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 提交次数 | 0 | 1 | 0 | 3 | 0 | 0 |
| 首次提交时间 | 1:11:35 | 3:29:08 | ||||
| 首A时间 | 1:11:35 | |||||
| 最终通过数 | 0/48 | 1120/1258 | 462/557 | 805/1279 | 222/248 | 40/48 |
| 状态 | ✔ | ⚪补 | ||||
| 知识点 | 模拟+思维 | 二分+思维 |
| G | H | I | J | K | L | M | |
|---|---|---|---|---|---|---|---|
| 提交次数 | 1 | 0 | 0 | 0 | 0 | 0 | 5 |
| 首次提交时间 | 0:06:23 | 1:11:25 | |||||
| 首A时间 | 0:06:23 | 2:28:30 | |||||
| 最终通过数 | 1505/1533 | 248/309 | 531/702 | 6/19 | 44/98 | 186/241 | 1108/1281 |
| 状态 | ✔ | 补 | ✔ | ||||
| 知识点 | 数学规律 | 几何+思维+模拟+暴力(DP、数论也可解) | 模拟+数据结构 |
共 3 题,325m,Rk 313。
✔:比赛时通过;⚪:比赛时尝试过;补:已补题。
D - Walker
小评
赛后补题。赛时很容易的想到了二分,但是尴尬的点在于我们想的是对时间进行二分,然后分类讨论两个人的位置关系,这就导致代码很长,而且一直存在错误没有找到。
总体来说这是一道偏简单的题目,想到了正解之后代码极其精炼,且没有多少细节,能够很轻易的解决。
题意
长度为 \(N\) 的数轴上有两个人分别位于 \(x、y\) ,两个人的步行速度分别为 \(v_x、v_y\) ,在任何时刻他们都能转换方向,求解他们走遍整根数轴需要的最短时间。
思路
由于赛时主要是我在写,所以我补这道题将从赛时思路进行转换。
赛时思路(复杂)
设 \(A\) 为左边那个人,\(B\) 为右边那个人。
二分时间,对所有的情况进行讨论:\(A\) 向左、向右,\(B\) 向左、向右。
以 \(A\) 向左进行举例,有以下几种状态:
- \(A\) 向左跑,并停在 \(0、x\) 中间:此时 \(B\) 需要跑完全程;
- \(A\) 向左跑到 \(0\) ,并停在 \(0、x\) 中间:此时 \(B\) 最左到 \(x\) ,最右到 \(N\) ;
- \(A\) 向左跑到 \(0\) ,并停在 \(x、y\) 中间:此时 \(B\) 最左到 \(A\) ,最右到 \(N\) ;
- \(A\) 向左跑到 \(0\) ,并停在 \(y、N\) 中间:此时 \(B\) 要停止在 \(N\) ;
- \(A\) 向左跑到 \(0\) 、再向右跑到 \(N\) 后停止:此时 \(B\) 不需要移动。
再以 \(A\) 向右进行举例:
- \(A\) 向右跑,并停在 \(x、N\) 中间:此时 \(B\) 需要跑完全程;
- \(A\) 向右跑,并于 \(x、N\) 中间的某处停止,再向左跑至 \(0\) (即 \(A、B\) 相遇);
- \(A\) 向右跑到 \(N\) ,并停在 \(0、N\) 的中间:此时 \(B\) 要停止在 \(0\) ;
- \(A\) 向右跑到 \(N\) 、再向左跑到 \(0\) 后停止:此时 \(B\) 不需要移动。
而上面的方法只是固定了 \(A\) 的行踪,而对于相对应的 \(B\) 的行踪,还需要进一步分类讨论。最后经重构发现,最少只需要分别讨论“ \(A\) 向左”“ \(B\) 向右”和“\(A\) 向右”这三种情况即可。
正解
设 \(A\) 为左边那个人,\(B\) 为右边那个人。
两个人有如下几种方式走遍整根数轴:
- \(A\) 或者 \(B\) 一个人跑完;
- \(A、B\) 向着对方的方向一直走,直到边界;
- \(A、B\) 最终在中间的某一个点碰到(且这个位置一定在 \(x、y\) 之间)。
以上前两种情况可以直接得解,最后一种情况可以通过二分碰到的位置得解。
AC代码
赛时思路
点击查看代码
double n, x, vx, y, vy, walk_a, walk_b;
bool check_Atol(double t) {
double lenA = t * vx, lenB = t * vy;
double walkA = lenA - x;
if (lenA < x) { //A向左跑跑不到0:
if (y + n <= lenB) return true; //B跑全程
if ((n - y) + n <= lenB) return true; //B跑全程
}
else if (x <= lenA && lenA < 2 * x) { //A跑到0并停在x的左边:
if ((y - x) + (n - x) <= lenB) return true; //B向左跑到x,再向右跑到底
if ((n - y) + (n - x) <= lenB) return true; //B向右跑到n,再向左跑到x
}
else if (2 * x <= lenA && lenA < x + y) { //A停在x、y中间:
if ((y - walkA) + (n - walkA) <= lenB) return true; //B向左碰到A,再向右跑到底
if ((n - y) + (n - walkA) <= lenB) return true; //B向右跑到n,再向左碰到A
}
else if (x + y <= lenA && lenA < x + n) { //A停在y右侧:
if (y + n <= lenB) return true; //B跑全程
if (n - y <= lenB) return true; //B跑全程
}
else if (x + n <= lenA) { //A跑全程:
return true;
}
return false;
}
bool check_Btor(double t) {
double lenA = t * vx, lenB = t * vy;
double walkB = lenB - (n - y);
if (lenB < n - y) { //B向右跑跑不到n:
if ((n - x) + n <= lenA) return true; //A跑全程
if (x + n <= lenA) return true; //A跑全程
}
else if (n - y <= lenB && lenB < 2 * (n - y)) { //B跑到n并停在y的右边:
if ((y - x) + y <= lenA) return true; //A向右跑到y,再向左跑到0
if (x + y <= lenA) return true;
}
else if (2 * (n - y) <= lenB && lenB < (n - y) + (n - x)) { //B停在x、y中间:A向右碰到B,再向左跑到0
if ((n - walkB - x) + (n - walkB) <= lenA) return true;
if (x + (n - walkB) <= lenA) return true;
}
else if ((n - y) + (n - x) <= lenB && lenB < (n - y) + n) { //B停在x左侧:A跑全程
if (n - x + n <= lenA) return true;
if (x <= lenA) return true;
}
else if ((n - y) + n <= lenB) {
return true;
}
return false;
}
bool check_Ator(double t) {
double lenA = t * vx, lenB = t * vy;
if (lenA < n - x) {// A 向右跑,并停在 x、N 中间
if (y + n <= lenB) return true;
if (n - y + n <= lenB) return true;
}
else if (n - x <= lenA && lenA < n - x + n) { // A 向右跑到 N ,并停在 0、N 的中间
if (y <= lenB) return true;
if (n - y + n <= lenB) return true;
}
else { // A 向右跑到 N 、再向左跑到 0 后停止
return true;
}
if (x <= t * vx && n - y <= t * vy)
return n + (y - x) <= t * (vx + vy);
return false;
}
void Solve() {
cin >> n >> x >> vx >> y >> vy;
if (x > y) swap(x, y), swap(vx, vy);
double l, r, ans = INF;
l = 0, r = 1e18;
for (int i = 1; i <= 100; ++ i) {
double mid = (l + r) / 2;
if (check_Atol(mid) == true) r = mid;
else l = mid;
}
ans = min(ans, l);
l = 0, r = 1e18;
for (int i = 1; i <= 100; ++ i) {
double mid = (l + r) / 2;
if (check_Ator(mid) == true) r = mid;
else l = mid;
}
ans = min(ans, l);
l = 0, r = 1e18;
for (int i = 1; i <= 100; ++ i) {
double mid = (l + r) / 2;
if (check_Btor(mid) == true) r = mid;
else l = mid;
}
ans = min(ans, l);
cout << ans << endl;
}
正解
点击查看代码
double n, x, vx, y, vy;
double clac(double n, double x, double v) {
return min((n + x) / v, (n + n - x) / v); //分别计算x向左、向右跑需要的时间
}
void Solve() {
cin >> n >> x >> vx >> y >> vy;
if (x > y) swap(x, y), swap(vx, vy);
double ans = min(clac(n, x, vx), clac(n, y, vy)); //分别计算A, B跑完全程需要的时间
ans = min(ans, max((n - x) / vx, y / vy)); //分别计算A, B对穿需要的时间
double l = x, r = y, ansl = INF, ansr;
for (int i = 1; i <= 100; ++ i) {
double mid = (l + r) / 2;
ansl = clac(mid, x, vx);
ansr = clac(n - mid, y - mid, vy);
// _(mid, ansl, ansr);
if (ansl < ansr) l = mid;
else r = mid;
}
cout << min(ans, max(ansl, ansr)) << endl;
}
另附一组赛时代码的hack数据:
3
100 0 1 98 1
10000 898.090 0.123 8293.021 0.786
50.2 0 25 48 1.1
51.0000000000
13283.6979351032
2.0000000000
I - Sky Garden
小评
基础解析几何题,补完题之后感觉这就是纯纯打卡题,可惜赛时没开这道题。
题意
给出 \(N\) 个同心圆,半径从小到大依次为 \(1,2,3…,N\) ,给出 \(M\) 条直线,这些直线将同心圆分割成面积大小相同的 \(2*M\) 部分。圆和直线相交于一些点,构成集合 \(P\) ,现在请你求出集合中任何两个点的最短距离之和。
思路
分类讨论解
同一层问题:首先考虑同一个圆上的各点,固定起点,任选一个点作为起点 \(S\) ,我们发现,其到其的对称点 \(S'\) 的最短距离一定是直径,而其到其他点的最短距离则不确定,可能是直径,可能是弧线,所以需要暴力枚举判断,\(\mathcal O(N^2)\) 。计算出此时的答案 \(Ans_i\) 后,由于起点 \(S\) 可以变换 \(2*M\) 次,而每段距离都被计算了两遍,改变起点,所以最终答案是 \(\dfrac{2*M*Ans_i}{2}\) 。
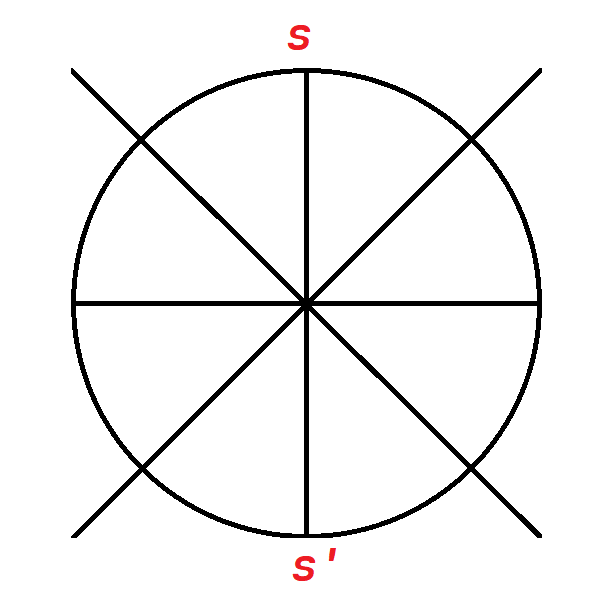
不同层问题:其次考虑不同圆上的各点,固定起点,依旧任选一个点作为起点 \(S\) ,我们发现,如果要跨圈,那么先走半径差 \(d\) 到达内层一定是更优的,内层一共有 \(2*M\) 个点,所以一共要走 \(2*M\) 遍半径差。而走完半径差后,剩下的内容就变成了起点固定的同一层问题,直接套用刚刚计算出的 \(Ans_{内圈}\) 即可,答案为 \(Ans_{内圈}+2*M*d\) 。改变起点,得到最终答案 \(2*M* \big(Ans_{内圈}+2*M*d \big)\) 。
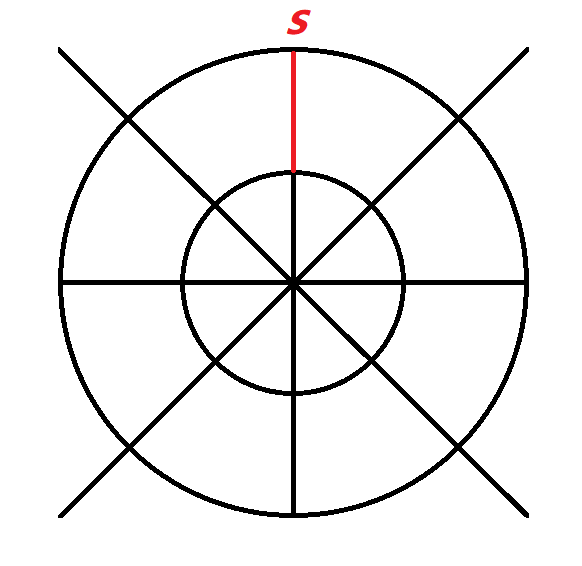
圆心问题:当 \(M>1\) 时会多出来一个圆心交点。
以上,总复杂度为 \(\mathcal O(N^2)\) ,本方法主要是通过同层、不同层的讨论,直接用 \(Ans[]\) 优化了原 \(\mathcal O(N^3)\) 的一维。
线性解
这个解法实际上可以看作是上述方法的再优化,这里我大胆猜想一下优化方式:
- 同一层判断走弧还是走直径:有 \(\displaystyle X= 2* \left \lfloor \frac{2r}{tem} \right \rfloor=2*\left \lfloor 2r / \frac{2\pi r}{2m} \right \rfloor =\left \lfloor \frac{2m}{\pi} \right \rfloor\) 个点是需要走弧线的,剩下的 \(2*M-X\) 个点全部走直径,套用高斯公式可以将同层的答案算出;
- 跨一层的答案计算:由于半径差固定,所以答案差也固定,可以分别计算走弧线和走直径的点比上一层少走了多少距离,此后所有跨一层省下来的距离都相同,故直接乘 \(N-1\) 即可;
- 跨两层的答案计算:基本同上,这样跨层的答案计算又可以推出一个线性式子;
- 最后再特判一下圆心。
全部用线性式子替代,\(\mathcal O(1)\) 。
AC代码
分类讨论解
点击查看代码
namespace Geometry { //几何
using ld = long double;
const ld PI = acos(-1);
// cout << fixed << setprecision(12);
}
using namespace Geometry;
ld ans[N];
signed main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cout << fixed << setprecision(12);
int n, m; cin >> n >> m;
ld ANS = 0;
//同层
for (int i = 1; i <= n; ++ i) {
ld tem = PI * i / m; //单段弧长
for (int j = 1; j < m; ++ j) {
ans[i] += 2 * min(j * tem, (ld)2 * i); //判断是走弧近还是走中心近
}
ans[i] += 2 * i; //对面的点单独判断,且一定是走中心近
ANS += ans[i] * m;
}
//异层
for (int i = 1; i <= n; ++ i) {
for (int j = i + 1; j <= n; ++ j) {
ANS += (ans[i] + 2 * m * (j - i)) * 2 * m;
}
}
//中心点
if (m > 1) {
for (int i = 1; i <= n; ++ i) {
ANS += 2 * m * i;
}
}
cout << ANS;
return 0;
}
线性解(抄)
点击查看代码
const double pi = acos(-1);
int main() {
long double n, m, s = 0, k1, k2, t;
cin >> n >> m;
k1 = (1 + n) * n * n / 2 - n * (n + 1) * (2 * n + 1) / 6;
k2 = (1 + n) * n * (0.5 + n) / 2 - n * (n + 1) * (2 * n + 1) / 6;
s += (1 + n) * n * m;
if (m == 1) s = 0;
s += 4 * m * m * k1;
t = floor(2 * m / pi);
s += (2 * pi * t * (t + 1) + (4 * m * (m - t) - 2 * m) * 2) * k2;
cout << fixed << setprecision(10) << s;
}
后日谈
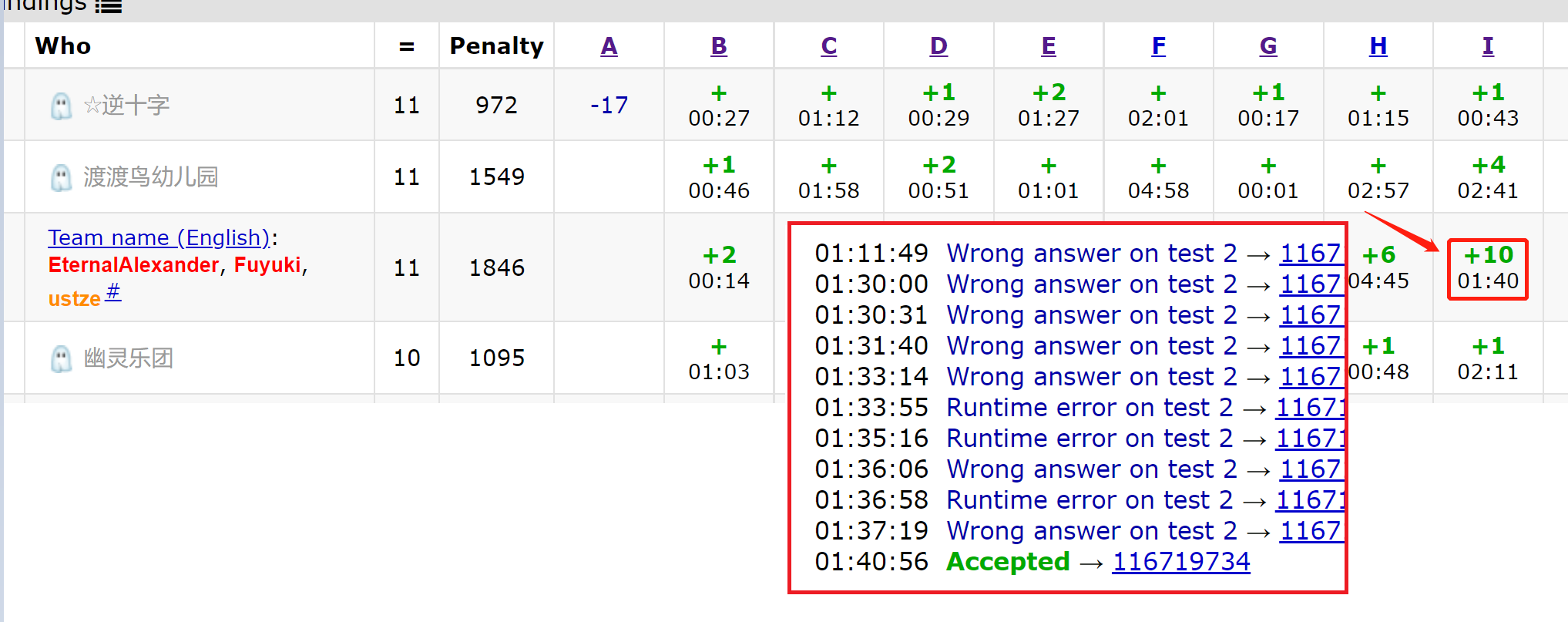
错误了一次,原因在于没有判断 \(M\) 是否大于 \(1\) 就计算了圆心,有点坑的是返回的错误点是WA2,即样例点2并非是数据2,我看到榜前有支队伍这道题炸掉了,估计也是因为没想到这一点的缘故吧,属实是有点坑了(乐)。
M - Gitignore
小评
\(\mathcal{Consider\ by\ \pmb {Wida}\ \&\ \pmb {Hamine}}\),\(\mathcal{Solved\ by\ \pmb {Hamine}}\) 。这道题我和 \(\mathcal Hamine\) 思路不一样,我完成的较快,但是一直WA,也查不出来错在哪,\(\mathcal Hamine\) 之前有看过这道题,一直在复原思路,导致写的比较慢,但是最后一发过了。
赛后反思,我写这道题时确实过于急躁了,在没有找到明确错误的时候贡献了四发罚时,属实不应该。赛后重构时轻易的找到了自己的错误,并且大致可以将自己赛时的思路完全推翻,属于是想了一个假算法。
本题最终由 \(\mathcal Hamine\) 使用 \(\tt map\) 这一数据结构通过,在看别人代码的时候我发现排名靠前的人都是使用字典树这一数据结构通过的。
题意
有 \(N\) 条文件路径,例如“C/wenjian/VP/102900M",记前面若干级为文件夹名,最后一级”102900M"为文件名。
- 现在,我们可以将前缀相同的路径进行合并,例如“C/wenjian/Luogu/1001”即可和上面的路径压合并成“C/wenjian”;
- 保证同一个文件夹中不存在子文件夹和文件名称相同,例如,不同时存在“C/wenjian/VP/102900M”和“C/wenjian”,因为这代表“C”中同时存在一个叫“wenjian”的子文件夹和一个叫“wenjian”的文件。
然而,有 \(M\) 个关键文件所在路径是不能被合并的,询问至多可以合并几条文件路径。
思路
赛时思路
暴力枚举 \(M\) 个关键文件所在路径的全部前缀子路径,在 \(\tt map\) 中标记为 \(1\) ,代表所有这些子路径均不能被合并。
先假设全部路径均不能被合并,\(ans=N\) ;随后暴力枚举 \(N\) 个文件路径的全部前缀子路径:
- 如果某条子路径在 \(\tt map\) 中被标记为 \(1\) ,说明不能被合并,继续枚举;
- 如果某条子路径在 \(\tt map\) 中未被标记过,说明这条子路径是第一次出现,不能被合并,标记为 \(2\) ;
- 如果某条子路径在 \(\tt map\) 中被标记为 \(2\) ,说明这条子路径已经出现过了,那么原文件路径就可以被合并掉,即将 \(ans-1\) ,然后跳过剩下子路径的枚举,直接跳转至下一条原文件路径;
在补题时我对“跳过剩下子路径的枚举”产生了怀疑,实际上这里是一个优化了,也可以不做这个优化,再引入一个诸如 \(\tt set\) 的数据结构作为辅助。优化的必要性稍加思考能够得解,这里不再单独描述。
AC代码
点击查看代码
string s[N];
void Solve() {
int n, m; cin >> n >> m;
map<string, int> dic;
for (int i = 1; i <= n + m; ++ i) {
cin >> s[i];
}
for (int i = 1; i <= m; ++ i) {
string t;
for (auto j : s[i + n]) {
t += j;
if (j == '/') dic[t] = 1; //枚举被禁止压缩路径的每一种子路径,这些子路径都被禁止压缩
}
}
int ans = n; //初始时全部路径均不能被压缩
for (int i = 1; i <= n; ++ i) {
string t;
for (auto j : s[i]) {
t += j;
if (j != '/') continue;
if (dic[t] == 1) continue; //说明这个路径是被禁止压缩的,直接跳过
else if (dic[t] == 0) dic[t] = 2; //说明这个路径是第一次出现,记录
else if (dic[t] == 2) { //说明这个路径已经不是第一次出现了,那么就可以被压缩掉
-- ans;
break;
}
}
}
cout << ans << endl;
}
另附一组赛时代码的hack数据:
2
3 0
a/b/cc/e
a/b/dd/e
a/b/c
3 1
a/b/cc/e
a/b/dd/e
a/b/c
a/b/c
1
3



 浙公网安备 33010602011771号
浙公网安备 33010602011771号