【XCPC模板整理 - 第三期】几何
- 前言
- 语法说明
- 必要初始化
- 角度与弧度
- 平面点线相关
- 平面圆相关(使用浮点数处理)
- 平面三角形相关(使用浮点数处理)
- 平面方程转换
- 平面多边形(未整理)
- 二维凸包
- 三维必要初始化
- 三维点线面相关
- 空间三点是否共线 onLine
- 四点是否共面 onPlane
- 空间点是否在线段上 pointOnSegment
- 空间两点是否在线段同侧 pointOnSegmentSide
- 两点是否在平面同侧 pointOnPlaneSide
- 空间两直线是否平行 lineParallel
- 两平面是否平行 planeParallel
- 空间两直线是否是同一条 Same
- 两平面是否是同一个 Same
- 直线是否与平面平行 linePlaneParallel
- 空间两直线是否垂直 lineVertical
- 两平面是否垂直 planeVertical
- 空间两线段是否相交
- 空间两直线是否相交及交点 lineIntersection
- 直线与平面是否相交及交点 linePlaneCross
- 两平面是否相交及交线 planeIntersection
- 点到直线的最近点与最近距离 pointToLine
- 点到平面的最近点与最近距离 pointToPlane
- 空间两直线的最近距离与最近点对
- 三维角度与弧度
- 空间多边形
- 常用例题
- 常用结论
- 本文参考列表
前言
本文 GitHub链接 。
点击查看
关于文章
这是我个人使用的一些模板封装。本文是我迄今为止写过的专业性最强的文章,全文内容均为原创或经过我的二次修改整理,如需转载,请务必注意文末的版权信息声明与引用信息。
限于个人能力,可能存在诸多不足与漏洞,在未加测试直接使用前请务必小心谨慎。更新可能会滞后于我本地的文档,如有疑问或者催更之类的可以在评论区留言。
全文模板测试均基于以下版本信息,请留意版本兼容问题。
Windows, 64bit
G++ (ISO C++20)
stack=268435456
开启O2优化
同时,可能还使用到了如下宏定义:
#define int long long
#define endl "\n"
using LL = long long;
using ld = long double;
using PII = pair<int, int>;
using TII = tuple<int, int, int>;
文章大部分内容为模板封装,少部分内容为经典例题、未进行封装。
关于约定俗成
本文全部函数名均采用小驼峰命名法,即除第一个单词之外,其他单词首字母均大写。
如无特别说明,本文中提到的点、直线指代二维点、二维直线。如果与“空间”、“平面”同时出现,则指代三维点、三维直线。
如无特别说明,本文中默认构成直线的两个点不共点、构成平面的三个点不共线(即输入合法),然而,在cp中出题人往往不保证输入合法,请按照题意进行扩展判断。
为了保证正确性,函数都经过了我个人手造数据做的初步测试,为了方便大家进一步测试,我将一部分测试数据进行了上传,同时尽可能的附上了几何图像,位于折叠代码部分。
关于浮点数
这一部分可以辅助参考我的另一篇博客 算法笔记——奇技淫巧 # 浮点数误差。
-
由于 IEEE 754 规定
long double的精度不少于double的精度,主流的编程竞赛平台\(^{\text{注}}\)也确实做到了这一点,故个人习惯使用long double代替double;但是显然,更高的精度会导致运行时间变慢,请谨慎抉择。(\(^{\text{注}}\):在现版本的杭电OJ,某些情况下long double的精度不如double)。 -
浮点数整数和小数部分共享精度,所以在计算时,整数部分越大,小数部分精度越差。一般我们默认在数据集超过 \(10^6\) 时不再使用浮点数进行运算,否则会出现很严重的精度误差。
-
读入浮点数的速度非常慢,在大量读入浮点数、需要卡常的情况下,为了加快读入速度,一般我们默认不直接读入浮点数:对于整数输入,我们一般采取先读入整数后转换成浮点数的方式;对于浮点数输入,我们一般采取先读入字符串后转换成浮点数的方式。当输入量在 \(10^5\) 量级时,这样做可以快 \(10\) 倍(使用 例题 进行测试)。
-
读入浮点数会出现精度误差,我时常看到有人在代码中对某一些变量采取诸如
+= 1E-14的调整操作,最终以极短的代码与误差过题(此处 参考,这一份代码对r变量进行了调整操作,但是经我测试将偏移量修改为+= 1E-15就无法过题),由于我实在是没能弄明白这究竟是基于数据集采取的卡精度手段还是能被广泛运用的编程技巧,故暂时我也没法给出一个合适的结论。
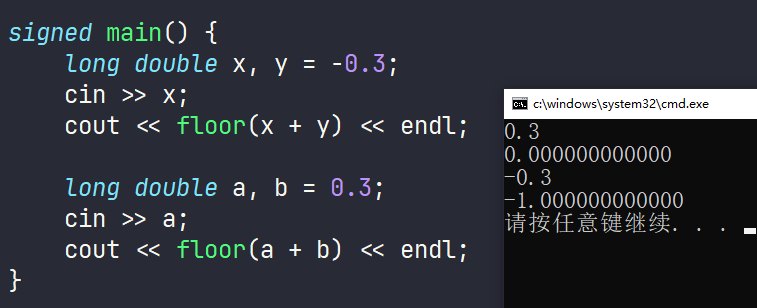

- 由于浮点数四则运算存在严重误差,故一般我们默认不直接对浮点数进行大小比较、也不直接对浮点数进行符号判断(下方模板有专门的比较函数)。
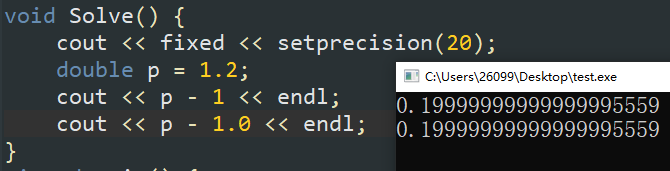
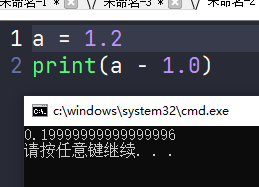
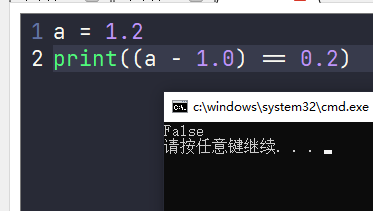
关于库函数
我们都知道有一些库函数有专门针对浮点数的版本,例如:绝对值函数 abs 的浮点数版本 fabs、开根号函数 sqrt 的浮点数版本 sqrtf,但是一般情况下浮点数版本都不如标准版,所以非特殊标注,我们一般都只使用标准版本。
关于拓展性
使用可变类型封装可以最大限度的保证代码的可拓展性,例如,对于不需要使用浮点数的题目,可以只进行整数运算;再例如,对于需要精确计算的题目,可以引入自定义的分数封装、大整数类封装或者 __int128 类型。然而,这样做的代价是,如果你不熟悉模板,很有可能导致出现不应该出现的隐式转换,对此我也非常苦恼,最终采用了折中方案,决定二维使用可变类型封装,三维固定为浮点数计算,同时,对于刚需浮点数的函数,我会给出提示。我也不知道这个决定会导致出现怎样的后果,但目前来看一切还算正常。
如果你不在意浮点数带来的各种问题,可以直接将全部可变类型封装修改为浮点数。
关于版权信息
我非常看重版权保护。
但是,知识无价,所以我欢迎大家进行学习转载。
语法说明
点击查看
初始化
使用重构函数来实现初始化。
struct Point {
int x, y;
Point(int _x = 0, _y = 0) : x(_x), y(_y) {}
};
可变类型封装
使用可变类型封装来实现类型转变。
struct PointOld { 固定变量类型
int x, y;
};
template <class T> struct PointNew { // 可变类型封装
T x, y;
};
int main() {
PointOld p = {1, 2};
PointNew<int> p1 = {1, 2};
PointNew<double> p2 = {1.2, 2.4};
}
自动类型转换
如果目标函数声明了变量类型,则据此自动匹配可变类型封装中的变量类型。这样写的好处是可以少些一些代码,但是缺点在于自动匹配过程不会报错,强制类型转换会导致数值变化。
template <class T> struct Point {
T x, y;
Point(T x_ = 0, T y_ = 0) : x(x_), y(y_) {}
template <class U> operator Point<U>() { // 自动类型匹配
return Point<U>(U(x), U(y));
}
};
void out(Point<double> p) {
cout << p.x << " " << p.y << endl;
}
signed main() {
out(Point{12, 14});
}
下方展示了一个由强制类型转换导致的问题,例中将 double 型转换为 int 型导致小数部分被舍弃。
template <class T> struct Point {
T x, y;
Point(T x_ = 0, T y_ = 0) : x(x_), y(y_) {}
template <class U> operator Point<U>() { // 自动类型匹配
return Point<U>(U(x), U(y));
}
};
void out(Point<int> p) {
cout << p.x << " " << p.y << endl;
}
signed main() {
out(Point{12.12, 14.5}); // 输出结果为 12 14
}
如果不使用此函数,那么就必须手动进行变量类型转换。
template <class T> struct Point {
T x, y;
Point(T x_ = 0, T y_ = 0) : x(x_), y(y_) {}
};
void out(Point<double> p) {
cout << p.x << " " << p.y << endl;
}
signed main() {
out(Point<double>{12, 14}); // 注意这里需要写 double,不然就会报错~
}
必要初始化
常用宏定义
using ld = long double;
const ld PI = acos(-1);
const ld EPS = 1e-7;
const ld INF = 1E18;
#define cc(x) cout << fixed << setprecision(x);
实数域 gcd
这里的 fmod 用于获取浮点数相除的余数,是库函数。
ld fgcd(ld x, ld y) { // 实数域gcd
return abs(y) < EPS ? abs(x) : fgcd(y, fmod(x, y));
}
判断两个浮点数是否相等(代替 == 运算)
template<class T, class S> bool equal(T x, S y) {
return -EPS < x - y && x - y < EPS;
}
判断浮点数的符号以及其是否为零
template<class T> int sign(T x) {
if (-EPS < x && x < EPS) return 0;
return x < 0 ? -1 : 1;
}
字符串读入浮点数
const int Knum = 4;
int read(int k = Knum) {
string s;
cin >> s;
int num = 0;
int it = s.find('.');
if (it != -1) { // 存在小数点
num = s.size() - it - 1; // 计算小数位数
s.erase(s.begin() + it); // 删除小数点
}
for (int i = 1; i <= k - num; i++) { // 补全小数位数
s += '0';
}
return stoi(s);
}
平面数据结构
自定义四则运算。
template<class T> struct Point { // 在C++17下使用emplace_back绑定可能会导致CE!
T x, y;
Point(T x_ = 0, T y_ = 0) : x(x_), y(y_) {} // 初始化
template<class U> operator Point<U>() { // 自动类型匹配
return Point<U>(U(x), U(y));
}
Point &operator+=(Point p) & { return x += p.x, y += p.y, *this; }
Point &operator+=(T t) & { return x += t, y += t, *this; }
Point &operator-=(Point p) & { return x -= p.x, y -= p.y, *this; }
Point &operator-=(T t) & { return x -= t, y -= t, *this; }
Point &operator*=(T t) & { return x *= t, y *= t, *this; }
Point &operator/=(T t) & { return x /= t, y /= t, *this; }
Point operator-() const { return Point(-x, -y); }
friend Point operator+(Point a, Point b) { return a += b; }
friend Point operator+(Point a, T b) { return a += b; }
friend Point operator-(Point a, Point b) { return a -= b; }
friend Point operator-(Point a, T b) { return a -= b; }
friend Point operator*(Point a, T b) { return a *= b; }
friend Point operator*(T a, Point b) { return b *= a; }
friend Point operator/(Point a, T b) { return a /= b; }
friend bool operator<(Point a, Point b) {
return equal(a.x, b.x) ? a.y < b.y - EPS : a.x < b.x - EPS;
}
friend bool operator>(Point a, Point b) { return b < a; }
friend bool operator==(Point a, Point b) { return !(a < b) && !(b < a); }
friend bool operator!=(Point a, Point b) { return a < b || b < a; }
friend auto &operator>>(istream &is, Point &p) {
return is >> p.x >> p.y;
}
friend auto &operator<<(ostream &os, Point p) {
return os << "(" << p.x << ", " << p.y << ")";
}
};
template<class T> struct Line {
Point<T> a, b;
Line(Point<T> a_ = Point<T>(), Point<T> b_ = Point<T>()) : a(a_), b(b_) {}
template<class U> operator Line<U>() { // 自动类型匹配
return Line<U>(Point<U>(a), Point<U>(b));
}
friend auto &operator<<(ostream &os, Line l) {
return os << "<" << l.a << ", " << l.b << ">";
}
};
数据结构简写宏定义
#define Pt Point<T> // 简写
#define Pi Point<int>
#define Pd Point<ld>
#define Lt Line<T>
#define Li Line<int>
#define Ld Line<ld>
叉乘
定义公式 \(a\times b=|a||b|\sin \theta\) ,可以用于计算角度。
template<class T> T cross(Point<T> a, Point<T> b) { // 叉乘
return a.x * b.y - a.y * b.x;
}
template<class T> T cross(Point<T> p1, Point<T> p2, Point<T> p0) { // 叉乘 (p1 - p0) x (p2 - p0);
return cross(p1 - p0, p2 - p0);
}
点乘
定义公式 \(a\times b=|a||b|\cos \theta\) 。
template<class T> T dot(Point<T> a, Point<T> b) { // 点乘
return a.x * b.x + a.y * b.y;
}
template<class T> T dot(Point<T> p1, Point<T> p2, Point<T> p0) { // 点乘 (p1 - p0) * (p2 - p0);
return dot(p1 - p0, p2 - p0);
}
欧几里得距离公式
最常用的距离公式。需要注意,开根号会丢失精度,如无强制要求,先不要开根号,留到最后一步一起开。
template <class T> ld dis(T x1, T y1, T x2, T y2) {
ld val = (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
return sqrt(val);
}
template <class T> ld dis(Point<T> a, Point<T> b) {
return dis(a.x, a.y, b.x, b.y);
}
欧几里得距离公式无开根号版
template <class T> T disEx(T x1, T y1, T x2, T y2) { // dis无开根版
T val = (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
return val;
}
template <class T> T disEx(Point<T> a, Point<T> b) { // dis无开根版
return disEx(a.x, a.y, b.x, b.y);
}
曼哈顿距离公式
template <class T> T dis1(Point<T> a, Point<T> b) { // 曼哈顿距离公式
return abs(a.x - b.x) + abs(a.y - b.y);
}
将向量转换为单位向量
需要注意,由于涉及除法,该函数刚需浮点数。
Point<ld> standardize(Point<ld> vec) { // 转换为单位向量
return vec / sqrt(vec.x * vec.x + vec.y * vec.y);
}
向量旋转
将当前向量移动至原点后顺时针旋转 \(90^{\circ}\) ,即获取垂直于当前向量的、起点为原点的向量。在计算垂线时非常有用。
例如,要想获取点 \(a\) 绕点 \(o\) 顺时针旋转 \(90^{\circ}\) 后的点,可以这样书写代码:auto ans = o + rotate(o, a); ;如果是逆时针旋转,那么只需更改符号即可:auto ans = o - rotate(o, a); 。例题 。
template<class T> Point<T> rotate(Point<T> a, Point<T> b) { // 旋转
Point<T> vec = a - b;
return {-vec.y, vec.x};
}
角度与弧度
弧度角度相互转换
ld toDeg(ld x) { // 弧度转角度
return x * 180 / PI;
}
ld toArc(ld x) { // 角度转弧度
return PI / 180 * x;
}
正弦定理
\(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\) ,其中 \(R\) 为三角形外接圆半径;
余弦定理(已知三角形三边,求角)
\(\cos C=\dfrac{a^2+b^2-c^2}{2ab},\cos B=\dfrac{a^2+c^2-b^2}{2ac},\cos A=\dfrac{b^2+c^2-a^2}{2bc}\)。可以借此推导出三角形面积公式 \(S_{\triangle ABC}=\dfrac{ab\cdot\sin C}{2}=\dfrac{bc\cdot\sin A}{2}=\dfrac{ac\cdot\sin B}{2}\)。
注意,计算格式是:由 \(b,c,a\) 三边求 \(\angle A\);由 \(a, c, b\) 三边求 \(\angle B\);由 \(a, b, c\) 三边求 \(\angle C\)。
ld angle(ld a, ld b, ld c) { // 余弦定理
ld val = acos((a * a + b * b - c * c) / (2.0 * a * b)); // 计算弧度
return val;
}
求两向量的夹角
能够计算 \([0^{\circ},180^{\circ}]\) 区间的角度。
ld angle(Point<ld> a, Point<ld> b) {
ld val = abs(cross(a, b));
return abs(atan2(val, a.x * b.x + a.y * b.y));
}
向量旋转任意角度
逆时针旋转,转换公式:\(\left\{\begin{matrix} x'=x\cos \theta-y\sin \theta \\ y'=x\sin \theta+y\cos \theta \end{matrix}\right.\)
Point<ld> rotate(Point<ld> p, ld rad) {
return {p.x * cos(rad) - p.y * sin(rad), p.x * sin(rad) + p.y * cos(rad)};
}
点绕点旋转任意角度
逆时针旋转,转换公式:\(\left\{\begin{matrix} x'=(x_0-x_1)\cos\theta+(y_0-y_1)\sin\theta+x_1 \\ y'=(x_1-x_0)\sin\theta+(y_0-y_1)\cos\theta+y_1 \end{matrix}\right.\)
Point<ld> rotate(Point<ld> a, Point<ld> b, ld rad) {
ld x = (a.x - b.x) * cos(rad) + (a.y - b.y) * sin(rad) + b.x;
ld y = (b.x - a.x) * sin(rad) + (a.y - b.y) * cos(rad) + b.y;
return {x, y};
}
平面点线相关
点是否在直线上(三点是否共线)
例题。
template<class T> bool onLine(Point<T> a, Point<T> b, Point<T> c) {
return sign(cross(b, a, c)) == 0;
}
template<class T> bool onLine(Point<T> p, Line<T> l) {
return onLine(p, l.a, l.b);
}
点是否在向量(直线)左侧 pointOnLineLeft
需要注意,向量的方向会影响答案;点在向量上时不视为在左侧。
template<class T> bool pointOnLineLeft(Pt p, Lt l) {
return cross(l.b, p, l.a) > 0;
}
两点是否在直线同侧
template<class T> bool pointOnLineSide(Pt p1, Pt p2, Lt vec) {
T val = cross(p1, vec.a, vec.b) * cross(p2, vec.a, vec.b);
return sign(val) == 1;
}
两点是否在线段异侧
例题。
template<class T> bool pointNotOnLineSide(Pt p1, Pt p2, Lt vec) {
T val = cross(p1, vec.a, vec.b) * cross(p2, vec.a, vec.b);
return sign(val) == -1;
}
两直线相交交点 lineIntersection
需要注意,由于涉及除法,该函数刚需浮点数。在使用前需要先判断直线是否平行。
Pd lineIntersection(Ld l1, Ld l2) {
ld val = cross(l2.b - l2.a, l1.a - l2.a) / cross(l2.b - l2.a, l1.a - l1.b);
return l1.a + (l1.b - l1.a) * val;
}
两直线是否平行 lineParallel
例题 。
template<class T> bool lineParallel(Lt p1, Lt p2) {
return sign(cross(p1.a - p1.b, p2.a - p2.b)) == 0;
}
两直线是否垂直 lineVertical
例题 。
template<class T> bool lineVertical(Lt p1, Lt p2) {
return sign(dot(p1.a - p1.b, p2.a - p2.b)) == 0;
}
两条直线是否相同 same
template<class T> bool same(Line<T> l1, Line<T> l2) {
return lineParallel(Line{l1.a, l2.b}, {l1.b, l2.a}) &&
lineParallel(Line{l1.a, l2.a}, {l1.b, l2.b}) && lineParallel(l1, l2);
}
点到直线的最近距离与最近点 pointToLine
需要注意,由于涉及的函数刚需浮点数,该函数也刚需浮点数。同时返回最近点与最近距离。
测试点信息
#1(正确性测试)
Pd A = {-1.0115029612094, 1.6400137143826};
Pd L1 = {8.7538878008814, 4.0201089538886};
Pd L2 = {0, 10};
交点应当为 (3.204126406332584, 7.81122088337617)
计算结果为 (3.204126406332583, 7.811220883376170)
距离应当为 7.473642277171156
计算结果为 7.473642277171155
误差可控
===
#2(误差测试)
Pd A = {6637.16814159288, -39874.081846799585};
Pd L1 = {179941.00294985253, 23084.994753410287};
Pd L2 = {74483.77581120945, 895068.205666317};
交点应当为 (184947.21509102578, -18309.351142223444)
计算结果为 (184947.215091025747626, -18309.351142223443359)
距离应当为 179609.3273008667
计算结果为 179609.327300866651370
误差可控
pair<Pd, ld> pointToLine(Pd p, Ld l) {
Pd ans = lineIntersection({p, p + rotate(l.a, l.b)}, l);
return {ans, dis(p, ans)};
}
如果只需要计算最近距离,下方的写法可以减少书写的代码量,效果一致。
template<class T> ld disPointToLine(Pt p, Lt l) {
ld ans = cross(p, l.a, l.b);
return abs(ans) / dis(l.a, l.b); // 面积除以底边长
}
点是否在线段上 pointOnSegment
如果点为线段的端点也视为在线段上。
template<class T> bool pointOnSegment(Pt p, Lt l) {
return sign(cross(p, l.a, l.b)) == 0 && min(l.a.x, l.b.x) <= p.x && p.x <= max(l.a.x, l.b.x) &&
min(l.a.y, l.b.y) <= p.y && p.y <= max(l.a.y, l.b.y);
}
如果不含端点。
template<class T> bool pointOnSegment(Pt p, Lt l) {
return pointOnSegment(p, l) && min(l.a.x, l.b.x) < p.x && p.x < max(l.a.x, l.b.x) &&
min(l.a.y, l.b.y) < p.y && p.y < max(l.a.y, l.b.y);
}
点到线段的最近距离与最近点 pointToSegment
需要注意,由于涉及的函数刚需浮点数,该函数也刚需浮点数。同时返回最近点与最近距离。例题 。
pair<Pd, ld> pointToSegment(Pd p, Ld l) {
if (sign(dot(p, l.b, l.a)) == -1) { // 特判到两端点的距离
return {l.a, dis(p, l.a)};
} else if (sign(dot(p, l.a, l.b)) == -1) {
return {l.b, dis(p, l.b)};
}
return pointToLine(p, l);
}
点在直线上的投影点(垂足) project
需要注意,由于涉及除法,强制浮点数计算。
测试点信息
#1(正确性测试)
Pd A = {6, 0};
Pd L1 = {1, 1};
Pd L2 = {5, 2};
结果应当为 (5.4705882352941, 2.1176470588235)
计算结果为 (5.470588235294118, 2.117647058823529)
ok!
Pd project(Pd p, Ld l) { // 投影
Pd vec = l.b - l.a;
ld r = dot(vec, p - l.a) / (vec.x * vec.x + vec.y * vec.y);
return l.a + vec * r;
}
线段的中垂线 midSegment
template<class T> Lt midSegment(Lt l) {
Pt mid = (l.a + l.b) / 2; // 线段中点
return {mid, mid + rotate(l.a, l.b)};
}
两线段是否相交及交点 segmentIntersection
该扩展版可以同时返回相交状态和交点,分为四种情况:\(0\) 代表不相交;\(1\) 代表普通相交;\(2\) 代表重叠(交于两个点);\(3\) 代表相交于端点。需要注意,部分运算可能会使用到直线求交点,此时务必保证变量类型为浮点数!
测试点信息
#1(正确性测试)
Pi A = {6, -1}, B = {5, 5};
Pi C = {1, 1}, D = {5, 2};
计算结果为 不相交
ok!
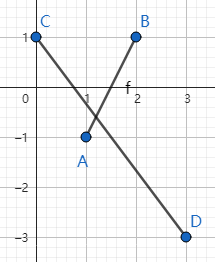
#2(正确性测试)
Pd A = {1, -1}, B = {2, 1};
Pd C = {0, 1}, D = {3, -3};
计算结果为 普通相交于 (1.2, -0.6) 和 (1.2, -0.6)
ok!
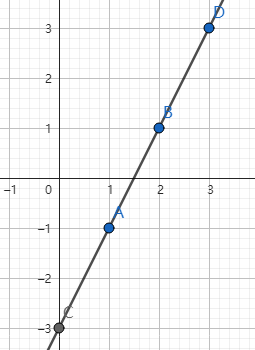
#3(正确性测试)
Pi A = {1, -1}, B = {2, 1};
Pi C = {0, -3}, D = {3, 3};
Pi A = {1, -1}, B = {2, 1};
Pi C = {0, -3}, D = {2, 1};
Pi A = {1, -1}, B = {2, 1};
Pi C = {1, -1}, D = {2, 1};
计算结果为 重叠,交叉于两点 (1, -1) 和 (2, 1)
ok!
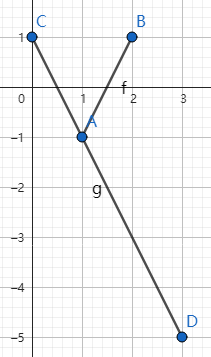
#3(正确性测试)
Pd A = {1, -1}, B = {2, 1};
Pd C = {0, 1}, D = {3, -5};
计算结果为 交叉于端点 (1.0, -1.0) 和 (1.0, -1.0)
ok!
注意!这里不使用浮点数会出现错误!
Pi A = {1, -1}, B = {2, 1};
Pi C = {0, 1}, D = {3, -5};
计算结果为 交叉于端点 (0, 1) 和 (0, 1)
wa!
template<class T> tuple<int, Pt, Pt> segmentIntersection(Lt l1, Lt l2) {
auto [s1, e1] = l1;
auto [s2, e2] = l2;
auto A = max(s1.x, e1.x), AA = min(s1.x, e1.x);
auto B = max(s1.y, e1.y), BB = min(s1.y, e1.y);
auto C = max(s2.x, e2.x), CC = min(s2.x, e2.x);
auto D = max(s2.y, e2.y), DD = min(s2.y, e2.y);
if (A < CC || C < AA || B < DD || D < BB) {
return {0, {}, {}};
}
if (sign(cross(e1 - s1, e2 - s2)) == 0) {
if (sign(cross(s2, e1, s1)) != 0) {
return {0, {}, {}};
}
Pt p1(max(AA, CC), max(BB, DD));
Pt p2(min(A, C), min(B, D));
if (!pointOnSegment(p1, l1)) {
swap(p1.y, p2.y);
}
if (p1 == p2) {
return {3, p1, p2};
} else {
return {2, p1, p2};
}
}
auto cp1 = cross(s2 - s1, e2 - s1);
auto cp2 = cross(s2 - e1, e2 - e1);
auto cp3 = cross(s1 - s2, e1 - s2);
auto cp4 = cross(s1 - e2, e1 - e2);
if (sign(cp1 * cp2) == 1 || sign(cp3 * cp4) == 1) {
return {0, {}, {}};
}
// 使用下方函数时请使用浮点数
Pd p = lineIntersection(l1, l2);
if (sign(cp1) != 0 && sign(cp2) != 0 && sign(cp3) != 0 && sign(cp4) != 0) {
return {1, p, p};
} else {
return {3, p, p};
}
}
如果不需要求交点,那么使用快速排斥+跨立实验即可,其中重叠、相交于端点均视为相交。
例题。
template<class T> bool segmentIntersection(Lt l1, Lt l2) {
auto [s1, e1] = l1;
auto [s2, e2] = l2;
auto A = max(s1.x, e1.x), AA = min(s1.x, e1.x);
auto B = max(s1.y, e1.y), BB = min(s1.y, e1.y);
auto C = max(s2.x, e2.x), CC = min(s2.x, e2.x);
auto D = max(s2.y, e2.y), DD = min(s2.y, e2.y);
return A >= CC && B >= DD && C >= AA && D >= BB &&
sign(cross(s1, s2, e1) * cross(s1, e1, e2)) == 1 &&
sign(cross(s2, s1, e2) * cross(s2, e2, e1)) == 1;
}
平面圆相关(使用浮点数处理)
点到圆的最近点
同时返回最近点与最近距离。需要注意,当点为圆心时,这样的点有无数个,此时我们视作输入错误,直接返回圆心。
测试点信息
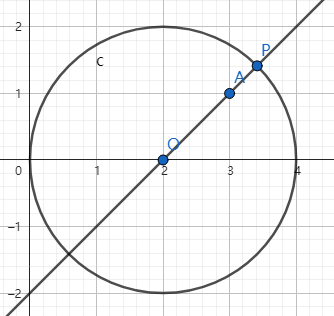
#1(正确性测试)
Pd A = {3, 1}, O = {2, 0};
ld r = 2;
交点应当为 (3.414213562373095, 1.414213562373095)
计算结果为 (3.414213562373095, 1.414213562373095)
距离应当为 0.5857864376269
计算结果为 0.585786437626905
ok!
pair<Pd, ld> pointToCircle(Pd p, Pd o, ld r) {
Pd U = o, V = o;
ld d = dis(p, o);
if (sign(d) == 0) { // p 为圆心时返回圆心本身
return {o, 0};
}
ld val1 = r * abs(o.x - p.x) / d;
ld val2 = r * abs(o.y - p.y) / d * ((o.x - p.x) * (o.y - p.y) < 0 ? -1 : 1);
U.x += val1, U.y += val2;
V.x -= val1, V.y -= val2;
if (dis(U, p) < dis(V, p)) {
return {U, dis(U, p)};
} else {
return {V, dis(V, p)};
}
}
根据圆心角获取圆上某点
将圆上最右侧的点以圆心为旋转中心,逆时针旋转 rad 度。
Point<ld> getPoint(Point<ld> p, ld r, ld rad) {
return {p.x + cos(rad) * r, p.y + sin(rad) * r};
}
直线是否与圆相交及交点
同时返回相交状态和交点,分为三种情况:\(0\) 代表不相交;\(1\) 代表相切;\(2\) 代表相交。
测试点信息
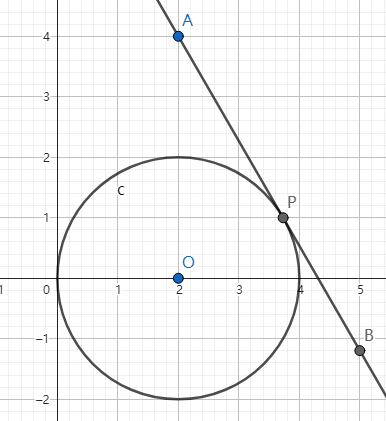
#1(正确性测试)
Pd A = {2, 4}, B = {5, -1.1961524227066};
Pd O = {2, 0};
ld r = 2;
答案应当为 相切于 (3.732050807569, 1.0)
计算结果为 相切于 (3.732050807568883, 1.000000000000009)
ok!
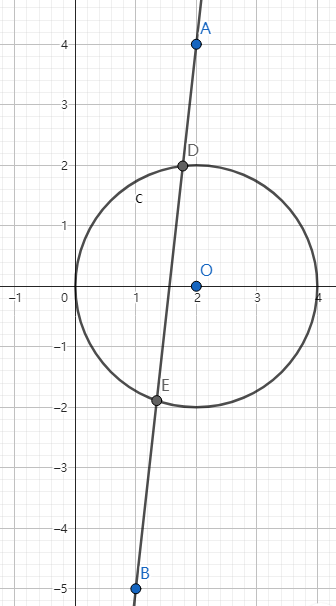
#2(正确性测试)
Pd A = {2, 4}, B = {1, -5};
Pd O = {2, 0};
ld r = 2;
答案应当为 相交于 (1.7763844113738, 1.9874597023646) 和 (1.3455668081383, -1.8898987267549)
计算结果为 相交于 (1.7763844113738, 1.9874597023646) 和 (1.3455668081383, -1.8898987267549)
ok!
tuple<int, Pd, Pd> lineCircleCross(Ld l, Pd o, ld r) {
Pd P = project(o, l);
ld d = dis(P, o), tmp = r * r - d * d;
if (sign(tmp) == -1) {
return {0, {}, {}};
} else if (sign(tmp) == 0) {
return {1, P, {}};
}
Pd vec = standardize(l.b - l.a) * sqrt(tmp);
return {2, P + vec, P - vec};
}
线段是否与圆相交及交点
同时返回相交状态和交点,分为四种情况:\(0\) 代表不相交;\(1\) 代表相切;\(2\) 代表相交于一个点;\(3\) 代表相交于两个点。
测试点信息同上。
tuple<int, Pd, Pd> segmentCircleCross(Ld l, Pd o, ld r) {
auto [type, U, V] = lineCircleCross(l, o, r);
bool f1 = pointOnSegment(U, l), f2 = pointOnSegment(V, l);
if (type == 1 && f1) {
return {1, U, {}};
} else if (type == 2 && f1 && f2) {
return {3, U, V};
} else if (type == 2 && f1) {
return {2, U, {}};
} else if (type == 2 && f2) {
return {2, V, {}};
} else {
return {0, {}, {}};
}
}
两圆是否相交及交点
同时返回相交状态和交点,分为四种情况:\(0\) 代表内含;\(1\) 代表相离;\(2\) 代表相切;\(3\) 代表相交。例题。
测试点信息
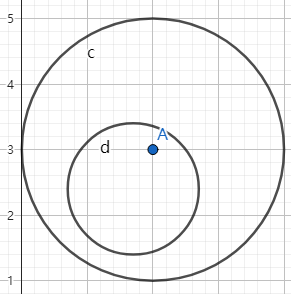
#1(正确性测试)
Pd O1 = {2, 3}, O2 = {1.7, 2.4};
ld r1 = 2, r2 = 1;
答案应当为 内含
计算结果为 内含
ok!

#2(正确性测试)
Pd O1 = {2, 3}, O2 = {7, 3};
ld r1 = 2, r2 = 1;
答案应当为 相离
计算结果为 相离
ok!
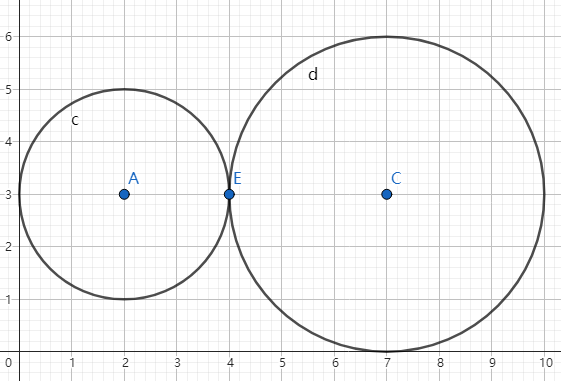
#3(正确性测试)
Pd O1 = {2, 3}, O2 = {7,3};
ld r1 = 2, r2 = 3;
答案应当为 相切于 (4, 3)
计算结果为 相切于 (4.0000000000000, 3.0000000000000)
ok!
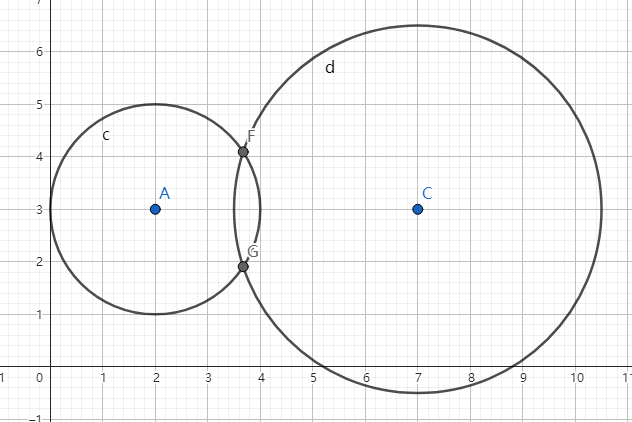
#4(正确性测试)
Pd O1 = {2, 3}, O2 = {7, 3};
ld r1 = 2, r2 = 3.5;
答案应当为 相交于 (3.675, 4.0928746497197) 和 (3.675, 1.9071253502803)
计算结果为 相交于 (3.6750000000000, 4.0928746497197) 和 (3.6750000000000, 1.9071253502803)
ok!
tuple<int, Pd, Pd> circleIntersection(Pd p1, ld r1, Pd p2, ld r2) {
ld x1 = p1.x, x2 = p2.x, y1 = p1.y, y2 = p2.y, d = dis(p1, p2);
if (sign(abs(r1 - r2) - d) == 1) {
return {0, {}, {}};
} else if (sign(r1 + r2 - d) == -1) {
return {1, {}, {}};
}
ld a = r1 * (x1 - x2) * 2, b = r1 * (y1 - y2) * 2, c = r2 * r2 - r1 * r1 - d * d;
ld p = a * a + b * b, q = -a * c * 2, r = c * c - b * b;
ld cosa, sina, cosb, sinb;
if (sign(d - (r1 + r2)) == 0 || sign(d - abs(r1 - r2)) == 0) {
cosa = -q / p / 2;
sina = sqrt(1 - cosa * cosa);
Point<ld> p0 = {x1 + r1 * cosa, y1 + r1 * sina};
if (sign(dis(p0, p2) - r2)) {
p0.y = y1 - r1 * sina;
}
return {2, p0, p0};
} else {
ld delta = sqrt(q * q - p * r * 4);
cosa = (delta - q) / p / 2;
cosb = (-delta - q) / p / 2;
sina = sqrt(1 - cosa * cosa);
sinb = sqrt(1 - cosb * cosb);
Pd ans1 = {x1 + r1 * cosa, y1 + r1 * sina};
Pd ans2 = {x1 + r1 * cosb, y1 + r1 * sinb};
if (sign(dis(ans1, p1) - r2)) ans1.y = y1 - r1 * sina;
if (sign(dis(ans2, p2) - r2)) ans2.y = y1 - r1 * sinb;
if (ans1 == ans2) ans1.y = y1 - r1 * sina;
return {3, ans1, ans2};
}
}
两圆相交面积
上述所言四种相交情况均可计算,之所以不使用三角形面积计算公式是因为在计算过程中会出现“负数”面积(扇形面积与三角形面积的符号关系会随圆的位置关系发生变化),故公式全部重新推导,这里采用的是扇形面积减去扇形内部的那个三角形的面积。例题。
ld circleIntersectionArea(Pd p1, ld r1, Pd p2, ld r2) {
ld x1 = p1.x, x2 = p2.x, y1 = p1.y, y2 = p2.y, d = dis(p1, p2);
if (sign(abs(r1 - r2) - d) >= 0) {
return PI * min(r1 * r1, r2 * r2);
} else if (sign(r1 + r2 - d) == -1) {
return 0;
}
ld theta1 = angle(r1, dis(p1, p2), r2);
ld area1 = r1 * r1 * (theta1 - sin(theta1 * 2) / 2);
ld theta2 = angle(r2, dis(p1, p2), r1);
ld area2 = r2 * r2 * (theta2 - sin(theta2 * 2) / 2);
return area1 + area2;
}
三点确定一圆
测试点信息

#1(正确性测试)
Pd A = {-2.28, 7};
Pd B = {1.76, 5};
Pd C = {2, 4.32};
圆心应当为 (-1.516880733945, 3.4611009174312)
计算结果为 (-1.5168807339450, 3.4611009174312)
半径应当为 3.6202427723608122
计算结果为 3.6202427723608
ok!
tuple<int, Pd, ld> getCircle(Pd A, Pd B, Pd C) {
if (onLine(A, B, C)) { // 特判三点共线
return {0, {}, 0};
}
Ld l1 = midSegment(Line{A, B});
Ld l2 = midSegment(Line{A, C});
Pd O = lineIntersection(l1, l2);
return {1, O, dis(A, O)};
}
求解点到圆的切线数量与切点
繁凡的模板这里貌似用错函数了,应该是抄Claris模板的时候认错函数名了(应该是 getPoint() 而非 rotate()),我将其改回来了。
pair<int, vector<Point<ld>>> tangent(Point<ld> p, Point<ld> A, ld r) {
vector<Point<ld>> ans; // 储存切点
Point<ld> u = A - p;
ld d = sqrt(dot(u, u));
if (d < r) {
return {0, {}};
} else if (sign(d - r) == 0) { // 点在圆上
ans.push_back(u);
return {1, ans};
} else {
ld ang = asin(r / d);
ans.push_back(getPoint(A, r, -ang));
ans.push_back(getPoint(A, r, ang));
return {2, ans};
}
}
求解两圆的内公、外公切线数量与切点
同时返回公切线数量以及每个圆的切点。
tuple<int, vector<Point<ld>>, vector<Point<ld>>> tangent(Point<ld> A, ld Ar, Point<ld> B, ld Br) {
vector<Point<ld>> a, b; // 储存切点
if (Ar < Br) {
swap(Ar, Br);
swap(A, B);
swap(a, b);
}
int d = disEx(A, B), dif = Ar - Br, sum = Ar + Br;
if (d < dif * dif) { // 内含,无
return {0, {}, {}};
}
ld base = atan2(B.y - A.y, B.x - A.x);
if (d == 0 && Ar == Br) { // 完全重合,无数条外公切线
return {-1, {}, {}};
}
if (d == dif * dif) { // 内切,1条外公切线
a.push_back(getPoint(A, Ar, base));
b.push_back(getPoint(B, Br, base));
return {1, a, b};
}
ld ang = acos(dif / sqrt(d));
a.push_back(getPoint(A, Ar, base + ang)); // 保底2条外公切线
a.push_back(getPoint(A, Ar, base - ang));
b.push_back(getPoint(B, Br, base + ang));
b.push_back(getPoint(B, Br, base - ang));
if (d == sum * sum) { // 外切,多1条内公切线
a.push_back(getPoint(A, Ar, base));
b.push_back(getPoint(B, Br, base + PI));
} else if (d > sum * sum) { // 相离,多2条内公切线
ang = acos(sum / sqrt(d));
a.push_back(getPoint(A, Ar, base + ang));
a.push_back(getPoint(A, Ar, base - ang));
b.push_back(getPoint(B, Br, base + ang + PI));
b.push_back(getPoint(B, Br, base - ang + PI));
}
return {a.size(), a, b};
}
平面三角形相关(使用浮点数处理)
三角形面积
ld area(Point<ld> a, Point<ld> b, Point<ld> c) {
return abs(cross(b, c, a)) / 2;
}
三角形外心
三角形外接圆的圆心,即三角形三边垂直平分线的交点。
template<class T> Pt center1(Pt p1, Pt p2, Pt p3) { // 外心
return lineIntersection(midSegment({p1, p2}), midSegment({p2, p3}));
}
三角形内心
三角形内切圆的圆心,也是三角形三个内角的角平分线的交点。其到三角形三边的距离相等。
Pd center2(Pd p1, Pd p2, Pd p3) { // 内心
#define atan2(p) atan2(p.y, p.x) // 注意先后顺序
Line<ld> U = {p1, {}}, V = {p2, {}};
ld m, n, alpha;
m = atan2((p2 - p1));
n = atan2((p3 - p1));
alpha = (m + n) / 2;
U.b = {p1.x + cos(alpha), p1.y + sin(alpha)};
m = atan2((p1 - p2));
n = atan2((p3 - p2));
alpha = (m + n) / 2;
V.b = {p2.x + cos(alpha), p2.y + sin(alpha)};
return lineIntersection(U, V);
}
三角形垂心
三角形的三条高线所在直线的交点。锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外。
Pd center3(Pd p1, Pd p2, Pd p3) { // 垂心
Ld U = {p1, p1 + rotate(p2, p3)}; // 垂线
Ld V = {p2, p2 + rotate(p1, p3)};
return lineIntersection(U, V);
}
三角形重心
求解三角形重心即为求解多边形重心,见后文《多边形重心》。
平面方程转换
浮点数计算直线的斜率
一般很少使用到这个函数,因为斜率的取值不可控(例如接近平行于 \(x,y\) 轴时)。需要注意,当直线平行于 \(y\) 轴时斜率为 inf 。
测试点信息
#1
Pd A = {0, 0};
Pd B = {-2.1245910913228,-7.220418987051};
目标函数应当为 y = 3.398498194095 * x
计算结果为 3.398498194095
一致
#2
Pd A = {-286055169.033697,-972154193.3725594};
Pd B = {944909746.2296575,964518549.227721};
目标函数应当为 y = 1.5732964592138 * x - 522104608.792032
计算结果 1.573296459214
误差可控
template <class T> ld slope(Pt p1, Pt p2) { // 斜率,注意 inf 的情况
return (p1.y - p2.y) / (p1.x - p2.x);
}
template <class T> ld slope(Lt l) {
return slope(l.a, l.b);
}
分数精确计算直线的斜率
调用分数四则运算精确计算斜率,返回最简分数,只适用于整数计算。
template<class T> Frac<T> slopeEx(Pt p1, Pt p2) {
Frac<T> U = p1.y - p2.y;
Frac<T> V = p1.x - p2.x;
return U / V; // 调用分数精确计算
}
分数运算类封装参考 【XCPC模板 - 个人模板封装】数据结构 # 分数运算类
两点式转一般式
返回由三个整数构成的方程,在输入较大时可能找不到较小的满足题意的一组整数解。可以处理平行于 \(x,y\) 轴、两点共点的情况。例题。
template<class T> tuple<int, int, int> getfun(Lt p) {
T A = p.a.y - p.b.y, B = p.b.x - p.a.x, C = p.a.x * A + p.a.y * B;
if (A < 0) { // 符号调整
A = -A, B = -B, C = -C;
} else if (A == 0) {
if (B < 0) {
B = -B, C = -C;
} else if (B == 0 && C < 0) {
C = -C;
}
}
if (A == 0) { // 数值计算
if (B == 0) {
C = 0; // 共点特判
} else {
T g = fgcd(abs(B), abs(C));
B /= g, C /= g;
}
} else if (B == 0) {
T g = fgcd(abs(A), abs(C));
A /= g, C /= g;
} else {
T g = fgcd(fgcd(abs(A), abs(B)), abs(C));
A /= g, B /= g, C /= g;
}
return tuple{A, B, C}; // Ax + By = C
}
一般式转两点式
由于整数点可能很大或者不存在,故直接采用浮点数,可以处理平行于 \(x,y\) 轴的情况,但是针对构不成方程的情况需要特判。例题(需结合两直线是否相同)。
Line<ld> getfun(int A, int B, int C) { // Ax + By = C
ld x1 = 0, y1 = 0, x2 = 0, y2 = 0;
if (A && B) { // 正常
if (C) {
x1 = 0, y1 = 1. * C / B;
y2 = 0, x2 = 1. * C / A;
} else { // 过原点
x1 = 1, y1 = 1. * -A / B;
x2 = 0, y2 = 0;
}
} else if (A && !B) { // 垂直
if (C) {
y1 = 0, x1 = 1. * C / A;
y2 = 1, x2 = x1;
} else {
x1 = 0, y1 = 1;
x2 = 0, y2 = 0;
}
} else if (!A && B) { // 水平
if (C) {
x1 = 0, y1 = 1. * C / B;
x2 = 1, y2 = y1;
} else {
x1 = 1, y1 = 0;
x2 = 0, y2 = 0;
}
} else { // 不合法,请特判
assert(false);
}
return {{x1, y1}, {x2, y2}};
}
抛物线与 x 轴是否相交及交点
使用浮点数求解,同时返回相交情况与交点。\(0\) 代表没有交点;\(1\) 代表相切;\(2\) 代表有两个交点。
tuple<int, ld, ld> getAns(ld a, ld b, ld c) {
ld delta = b * b - a * c * 4;
if (delta < 0.) {
return {0, 0, 0};
}
delta = sqrt(delta);
ld ans1 = -(delta + b) / 2 / a;
ld ans2 = (delta - b) / 2 / a;
if (ans1 > ans2) {
swap(ans1, ans2);
}
if (sign(delta) == 0) {
return {1, ans2, 0};
}
return {2, ans1, ans2};
}
平面多边形(未整理)
两向量构成的平面四边形有向面积
template<class T> T areaEx(Point<T> p1, Point<T> p2, Point<T> p3) {
return cross(b, c, a);
}
判断四个点能否组成矩形/正方形 isSquare
虽然不难,但是这个内容考察的很多,故干脆直接写成函数了,可以处理浮点数、共点的情况。返回分为三种情况:\(2\) 代表构成正方形;\(1\) 代表构成矩形;\(0\) 代表其他情况。例题1:判正方形与矩形,例题2:判矩形,例题3:判正方形。
template<class T> int isSquare(vector<Pt> x) {
sort(x.begin(), x.end());
if (equal(dis(x[0], x[1]), dis(x[2], x[3])) && sign(dis(x[0], x[1])) &&
equal(dis(x[0], x[2]), dis(x[1], x[3])) && sign(dis(x[0], x[2])) &&
lineParallel(Lt{x[0], x[1]}, Lt{x[2], x[3]}) &&
lineParallel(Lt{x[0], x[2]}, Lt{x[1], x[3]}) &&
lineVertical(Lt{x[0], x[1]}, Lt{x[0], x[2]})) {
return equal(dis(x[0], x[1]), dis(x[0], x[2])) ? 2 : 1;
}
return 0;
}
点是否在任意多边形内
射线法判定,\(t\) 为穿越次数,当其为奇数时即代表点在多边形内部;返回 \(2\) 代表点在多边形边界上。
template<class T> int pointInPolygon(Point<T> a, vector<Point<T>> p) {
int n = p.size();
for (int i = 0; i < n; i++) {
if (pointOnSegment(a, Line{p[i], p[(i + 1) % n]})) {
return 2;
}
}
int t = 0;
for (int i = 0; i < n; i++) {
auto u = p[i], v = p[(i + 1) % n];
if (u.x < a.x && v.x >= a.x && pointOnLineLeft(a, Line{v, u})) {
t ^= 1;
}
if (u.x >= a.x && v.x < a.x && pointOnLineLeft(a, Line{u, v})) {
t ^= 1;
}
}
return t == 1;
}
线段是否在任意多边形内部
template<class T>
bool segmentInPolygon(Line<T> l, vector<Point<T>> p) {
// 线段与多边形边界不相交且两端点都在多边形内部
#define L(x, y) pointOnLineLeft(x, y)
int n = p.size();
if (!pointInPolygon(l.a, p)) return false;
if (!pointInPolygon(l.b, p)) return false;
for (int i = 0; i < n; i++) {
auto u = p[i];
auto v = p[(i + 1) % n];
auto w = p[(i + 2) % n];
auto [t, p1, p2] = segmentIntersection(l, Line(u, v));
if (t == 1) return false;
if (t == 0) continue;
if (t == 2) {
if (pointOnSegment(v, l) && v != l.a && v != l.b) {
if (cross(v - u, w - v) > 0) {
return false;
}
}
} else {
if (p1 != u && p1 != v) {
if (L(l.a, Line(v, u)) || L(l.b, Line(v, u))) {
return false;
}
} else if (p1 == v) {
if (l.a == v) {
if (L(u, l)) {
if (L(w, l) && L(w, Line(u, v))) {
return false;
}
} else {
if (L(w, l) || L(w, Line(u, v))) {
return false;
}
}
} else if (l.b == v) {
if (L(u, Line(l.b, l.a))) {
if (L(w, Line(l.b, l.a)) && L(w, Line(u, v))) {
return false;
}
} else {
if (L(w, Line(l.b, l.a)) || L(w, Line(u, v))) {
return false;
}
}
} else {
if (L(u, l)) {
if (L(w, Line(l.b, l.a)) || L(w, Line(u, v))) {
return false;
}
} else {
if (L(w, l) || L(w, Line(u, v))) {
return false;
}
}
}
}
}
}
return true;
}
任意多边形的面积
template<class T> ld area(vector<Point<T>> P) {
int n = P.size();
ld ans = 0;
for (int i = 0; i < n; i++) {
ans += cross(P[i], P[(i + 1) % n]);
}
return ans / 2.0;
}
皮克定理
绘制在方格纸上的多边形面积公式可以表示为 \(S=n+\dfrac{s}{2}-1\) ,其中 \(n\) 表示多边形内部的点数、\(s\) 表示多边形边界上的点数。一条线段上的点数为 \(\gcd(|x_1-x_2|,|y_1-y_2|)+1\)。
任意多边形上的网格点个数(仅能处理整数)
皮克定理用。
int onPolygonGrid(vector<Point<int>> p) {
int n = p.size(), ans = 0;
for (int i = 0; i < n; i++) {
auto a = p[i], b = p[(i + 1) % n];
ans += gcd(abs(a.x - b.x), abs(a.y - b.y));
}
return ans;
}
任意多边形内部的网格点个数(仅能处理整数)
皮克定理用。
int inPolygonGrid(vector<Point<int>> p) {
int n = p.size(), ans = 0;
for (int i = 0; i < n; i++) {
auto a = p[i], b = p[(i + 1) % n], c = p[(i + 2) % n];
ans += b.y * (a.x - c.x);
}
ans = abs(ans);
return (ans - onPolygonGrid(p)) / 2 + 1;
}
二维凸包
获取二维静态凸包(Andrew算法)
flag 用于判定凸包边上的点、重复的顶点是否要加入到凸包中,为 \(0\) 时代表加入凸包(不严格);为 \(1\) 时不加入凸包(严格)。时间复杂度为 \(\mathcal O(N\log N)\) ,例题:洛谷模板题,例题。
template<class T> vector<Point<T>> staticConvexHull(vector<Point<T>> A, int flag = 1) {
int n = A.size();
if (n <= 2) { // 特判
return A;
}
vector<Point<T>> ans(n * 2);
sort(A.begin(), A.end());
int now = -1;
for (int i = 0; i < n; i++) { // 维护下凸包
while (now > 0 && cross(A[i], ans[now], ans[now - 1]) < flag) {
now--;
}
ans[++now] = A[i];
}
int pre = now;
for (int i = n - 2; i >= 0; i--) { // 维护上凸包
while (now > pre && cross(A[i], ans[now], ans[now - 1]) < flag) {
now--;
}
ans[++now] = A[i];
}
ans.resize(now);
return ans;
}
二维动态凸包
固定为 int 型,需要重新书写 Line 函数,cmp 用于判定边界情况。可以处理如下两个要求:
动态插入点 \((x,y)\) 到当前凸包中;
判断点 \((x,y)\) 是否在凸包上或是在内部(包括边界)。
template<class T> bool turnRight(Pt a, Pt b) {
return cross(a, b) < 0 || (cross(a, b) == 0 && dot(a, b) < 0);
}
struct Line {
static int cmp;
mutable Point<int> a, b;
friend bool operator<(Line x, Line y) {
return cmp ? x.a < y.a : turnRight(x.b, y.b);
}
friend auto &operator<<(ostream &os, Line l) {
return os << "<" << l.a << ", " << l.b << ">";
}
};
int Line::cmp = 1;
struct UpperConvexHull : set<Line> {
bool contains(const Point<int> &p) const {
auto it = lower_bound({p, 0});
if (it != end() && it->a == p) return true;
if (it != begin() && it != end() && cross(prev(it)->b, p - prev(it)->a) <= 0) {
return true;
}
return false;
}
void add(const Point<int> &p) {
if (contains(p)) return;
auto it = lower_bound({p, 0});
for (; it != end(); it = erase(it)) {
if (turnRight(it->a - p, it->b)) {
break;
}
}
for (; it != begin() && prev(it) != begin(); erase(prev(it))) {
if (turnRight(prev(prev(it))->b, p - prev(prev(it))->a)) {
break;
}
}
if (it != begin()) {
prev(it)->b = p - prev(it)->a;
}
if (it == end()) {
insert({p, {0, -1}});
} else {
insert({p, it->a - p});
}
}
};
struct ConvexHull {
UpperConvexHull up, low;
bool empty() const {
return up.empty();
}
bool contains(const Point<int> &p) const {
Line::cmp = 1;
return up.contains(p) && low.contains(-p);
}
void add(const Point<int> &p) {
Line::cmp = 1;
up.add(p);
low.add(-p);
}
bool isIntersect(int A, int B, int C) const {
Line::cmp = 0;
if (empty()) return false;
Point<int> k = {-B, A};
if (k.x < 0) k = -k;
if (k.x == 0 && k.y < 0) k.y = -k.y;
Point<int> P = up.upper_bound({{0, 0}, k})->a;
Point<int> Q = -low.upper_bound({{0, 0}, k})->a;
return sign(A * P.x + B * P.y - C) * sign(A * Q.x + B * Q.y - C) > 0;
}
friend ostream &operator<<(ostream &out, const ConvexHull &ch) {
for (const auto &line : ch.up) out << "(" << line.a.x << "," << line.a.y << ")";
cout << "/";
for (const auto &line : ch.low) out << "(" << -line.a.x << "," << -line.a.y << ")";
return out;
}
};
点与凸包的位置关系 contains
\(0\) 代表点在凸包外面;\(1\) 代表在凸壳上;\(2\) 代表在凸包内部。
template<class T> int contains(Point<T> p, vector<Point<T>> A) {
int n = A.size();
bool in = false;
for (int i = 0; i < n; i++) {
Point<T> a = A[i] - p, b = A[(i + 1) % n] - p;
if (a.y > b.y) {
swap(a, b);
}
if (a.y <= 0 && 0 < b.y && cross(a, b) < 0) {
in = !in;
}
if (cross(a, b) == 0 && dot(a, b) <= 0) {
return 1;
}
}
return in ? 2 : 0;
}
闵可夫斯基和
计算两个凸包合成的大凸包。
template<class T> vector<Point<T>> mincowski(vector<Point<T>> P1, vector<Point<T>> P2) {
int n = P1.size(), m = P2.size();
vector<Point<T>> V1(n), V2(m);
for (int i = 0; i < n; i++) {
V1[i] = P1[(i + 1) % n] - P1[i];
}
for (int i = 0; i < m; i++) {
V2[i] = P2[(i + 1) % m] - P2[i];
}
vector<Point<T>> ans = {P1.front() + P2.front()};
int t = 0, i = 0, j = 0;
while (i < n && j < m) {
Point<T> val = sign(cross(V1[i], V2[j])) > 0 ? V1[i++] : V2[j++];
ans.push_back(ans.back() + val);
}
while (i < n) ans.push_back(ans.back() + V1[i++]);
while (j < m) ans.push_back(ans.back() + V2[j++]);
return ans;
}
半平面交
计算多条直线左边平面部分的交集。
template<class T> vector<Point<T>> halfcut(vector<Line<T>> lines) {
sort(lines.begin(), lines.end(), [&](auto l1, auto l2) {
auto d1 = l1.b - l1.a;
auto d2 = l2.b - l2.a;
if (sign(d1) != sign(d2)) {
return sign(d1) == 1;
}
return cross(d1, d2) > 0;
});
deque<Line<T>> ls;
deque<Point<T>> ps;
for (auto l : lines) {
if (ls.empty()) {
ls.push_back(l);
continue;
}
while (!ps.empty() && !pointOnLineLeft(ps.back(), l)) {
ps.pop_back();
ls.pop_back();
}
while (!ps.empty() && !pointOnLineLeft(ps[0], l)) {
ps.pop_front();
ls.pop_front();
}
if (cross(l.b - l.a, ls.back().b - ls.back().a) == 0) {
if (dot(l.b - l.a, ls.back().b - ls.back().a) > 0) {
if (!pointOnLineLeft(ls.back().a, l)) {
assert(ls.size() == 1);
ls[0] = l;
}
continue;
}
return {};
}
ps.push_back(lineIntersection(ls.back(), l));
ls.push_back(l);
}
while (!ps.empty() && !pointOnLineLeft(ps.back(), ls[0])) {
ps.pop_back();
ls.pop_back();
}
if (ls.size() <= 2) {
return {};
}
ps.push_back(lineIntersection(ls[0], ls.back()));
return vector(ps.begin(), ps.end());
}
三维必要初始化
三维数据结构
自定义四则运算。由于三维大部分内容均涉及浮点数,故不再做可变类型区分。
struct Point3 {
ld x, y, z;
Point3(ld x_ = 0, ld y_ = 0, ld z_ = 0) : x(x_), y(y_), z(z_) {}
Point3 &operator+=(Point3 p) & {
return x += p.x, y += p.y, z += p.z, *this;
}
Point3 &operator-=(Point3 p) & {
return x -= p.x, y -= p.y, z -= p.z, *this;
}
Point3 &operator*=(Point3 p) & {
return x *= p.x, y *= p.y, z *= p.z, *this;
}
Point3 &operator*=(ld t) & {
return x *= t, y *= t, z *= t, *this;
}
Point3 &operator/=(ld t) & {
return x /= t, y /= t, z /= t, *this;
}
friend Point3 operator+(Point3 a, Point3 b) { return a += b; }
friend Point3 operator-(Point3 a, Point3 b) { return a -= b; }
friend Point3 operator*(Point3 a, Point3 b) { return a *= b; }
friend Point3 operator*(Point3 a, ld b) { return a *= b; }
friend Point3 operator*(ld a, Point3 b) { return b *= a; }
friend Point3 operator/(Point3 a, ld b) { return a /= b; }
friend auto &operator>>(istream &is, Point3 &p) {
return is >> p.x >> p.y >> p.z;
}
friend auto &operator<<(ostream &os, Point3 p) {
return os << "(" << p.x << ", " << p.y << ", " << p.z << ")";
}
};
struct Line3 {
Point3 a, b;
};
struct Plane {
Point3 u, v, w;
};
#define P3 Point3
#define L3 Line3
原点到当前点的距离计算
ld len(P3 p) {
return sqrt(p.x * p.x + p.y * p.y + p.z * p.z);
}
叉乘
三维的叉乘结果是一个点,为了与二维叉乘统一,我将函数名进行了修改。
P3 crossEx(P3 a, P3 b) {
P3 ans;
ans.x = a.y * b.z - a.z * b.y;
ans.y = a.z * b.x - a.x * b.z;
ans.z = a.x * b.y - a.y * b.x;
return ans;
}
ld cross(P3 a, P3 b) {
return len(crossEx(a, b));
}
点乘
ld dot(P3 a, P3 b) {
return a.x * b.x + a.y * b.y + a.z * b.z;
}
获取平面法向量
P3 getVec(Plane s) {
return crossEx(s.u - s.v, s.v - s.w);
}
三维欧几里得距离公式
ld dis(P3 a, P3 b) {
ld val = (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y) + (a.z - b.z) * (a.z - b.z);
return sqrt(val);
}
将三维向量转换为单位向量
P3 standardize(P3 vec) { // 转换为单位向量
return vec / len(vec);
}
三维点线面相关
空间三点是否共线 onLine
其中第二个函数是专门用来判断给定的三个点能否构成平面的,因为不共线的三点才能构成平面。
bool onLine(P3 p1, P3 p2, P3 p3) { // 三点是否共线
return sign(cross(p1 - p2, p3 - p2)) == 0;
}
bool onLine(Plane s) {
return onLine(s.u, s.v, s.w);
}
四点是否共面 onPlane
bool onPlane(P3 p1, P3 p2, P3 p3, P3 p4) { // 四点是否共面
ld val = dot(getVec({p1, p2, p3}), p4 - p1);
return sign(val) == 0;
}
空间点是否在线段上 pointOnSegment
bool pointOnSegment(P3 p, L3 l) {
return sign(cross(p - l.a, p - l.b)) == 0 && min(l.a.x, l.b.x) <= p.x &&
p.x <= max(l.a.x, l.b.x) && min(l.a.y, l.b.y) <= p.y && p.y <= max(l.a.y, l.b.y) &&
min(l.a.z, l.b.z) <= p.z && p.z <= max(l.a.z, l.b.z);
}
bool pointOnSegmentEx(P3 p, L3 l) { // pointOnSegment去除端点版
return sign(cross(p - l.a, p - l.b)) == 0 && min(l.a.x, l.b.x) < p.x &&
p.x < max(l.a.x, l.b.x) && min(l.a.y, l.b.y) < p.y && p.y < max(l.a.y, l.b.y) &&
min(l.a.z, l.b.z) < p.z && p.z < max(l.a.z, l.b.z);
}
空间两点是否在线段同侧 pointOnSegmentSide
当给定的两点与线段不共面、点在线段上时返回 \(false\) 。
bool pointOnSegmentSide(P3 p1, P3 p2, L3 l) {
if (!onPlane(p1, p2, l.a, l.b)) { // 特判不共面
return 0;
}
ld val = dot(crossEx(l.a - l.b, p1 - l.b), crossEx(l.a - l.b, p2 - l.b));
return sign(val) == 1;
}
两点是否在平面同侧 pointOnPlaneSide
点在平面上时返回 \(false\) 。
测试点信息
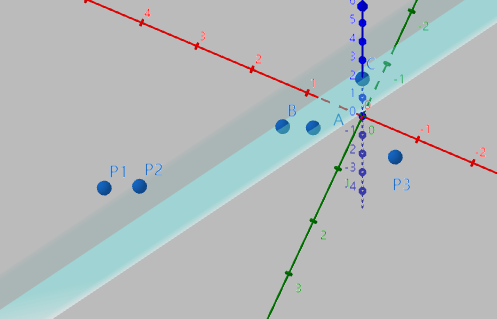
#1(正确性测试)
P3 A = {0, 2, 5};
P3 B = {1, 1, 1};
P3 C = {0, 0, 2};
Plane s = {A, B, C};
P3 P1 = {3.2, 3.32, 1.48};
P3 P2 = {2.4035, 3.67124, 3.56};
P3 P3 = {-1, 0.91, 1.62};
cout << pointOnPlaneSide(P1, P2, s) << endl; // 同侧
cout << pointOnPlaneSide(P1, P3, s) << endl; // 不同侧
ok!
bool pointOnPlaneSide(P3 p1, P3 p2, Plane s) {
ld val = dot(getVec(s), p1 - s.u) * dot(getVec(s), p2 - s.u);
return sign(val) == 1;
}
空间两直线是否平行 lineParallel
bool lineParallel(L3 l1, L3 l2) {
return sign(cross(l1.a - l1.b, l2.a - l2.b)) == 0;
}
两平面是否平行 planeParallel
bool planeParallel(Plane s1, Plane s2) {
ld val = cross(getVec(s1), getVec(s2));
return sign(val) == 0;
}
空间两直线是否是同一条 Same
bool same(L3 l1, L3 l2) {
return lineParallel(l1, l2) && lineParallel({l1.a, l2.b}, {l1.b, l2.a});
}
两平面是否是同一个 Same
bool same(Plane s1, Plane s2) {
return onPlane(s1.u, s2.u, s2.v, s2.w) && onPlane(s1.v, s2.u, s2.v, s2.w) &&
onPlane(s1.w, s2.u, s2.v, s2.w);
}
直线是否与平面平行 linePlaneParallel
bool linePlaneParallel(L3 l, Plane s) {
ld val = dot(l.a - l.b, getVec(s));
return sign(val) == 0;
}
空间两直线是否垂直 lineVertical
bool lineVertical(L3 l1, L3 l2) {
return sign(dot(l1.a - l1.b, l2.a - l2.b)) == 0;
}
两平面是否垂直 planeVertical
bool planeVertical(Plane s1, Plane s2) {
ld val = dot(getVec(s1), getVec(s2));
return sign(val) == 0;
}
空间两线段是否相交
测试点信息
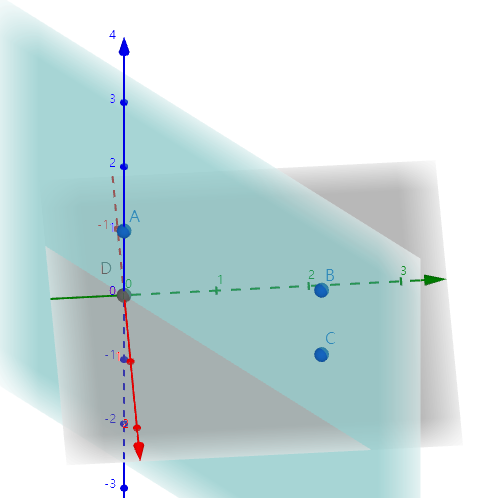
#1(正确性测试)
P3 A = {0,0, 1};
P3 B = {2, 2, 2};
P3 C = {2, 2, 1};
P3 D = {0, 0, 0};
cout << segmentIntersection({A, B}, {C, D}) << endl; // 不相交
cout << segmentIntersection({A, C}, {B, D}) << endl; // 相交
ok!
该版本重叠、相交于端点均视为相交。
bool segmentIntersection(L3 l1, L3 l2) {
if (!onPlane(l1.a, l1.b, l2.a, l2.b)) { // 特判不共面
return 0;
}
if (!onLine(l1.a, l1.b, l2.a) || !onLine(l1.a, l1.b, l2.b)) {
return !pointOnSegmentSide(l1.a, l1.b, l2) && !pointOnSegmentSide(l2.a, l2.b, l1);
}
return pointOnSegment(l1.a, l2) || pointOnSegment(l1.b, l2) || pointOnSegment(l2.a, l1) ||
pointOnSegment(l2.b, l2);
}
该版本重叠、相交于端点不视为相交。
bool segmentIntersection1(L3 l1, L3 l2) {
return onPlane(l1.a, l1.b, l2.a, l2.b) && !pointOnSegmentSide(l1.a, l1.b, l2) &&
!pointOnSegmentSide(l2.a, l2.b, l1);
}
空间两直线是否相交及交点 lineIntersection
当两直线不共面、两直线平行时返回 \(false\) 。
测试点信息

#1(正确性测试,数据集同上)
P3 A = {0, 0, 1};
P3 B = {2, 2, 2};
P3 C = {2, 2, 1};
P3 D = {0, 0, 0};
auto [a, b] = lineIntersection({A, B}, {C, D}); // 不相交
auto [c, d] = lineIntersection({A, C}, {B, D}); // 交于 (1.0, 1.0, 1.0)
ok!
pair<bool, P3> lineIntersection(L3 l1, L3 l2) {
if (!onPlane(l1.a, l1.b, l2.a, l2.b) || lineParallel(l1, l2)) {
return {0, {}};
}
auto [s1, e1] = l1;
auto [s2, e2] = l2;
ld val = 0;
if (!onPlane(l1.a, l1.b, {0, 0, 0}, {0, 0, 1})) {
val = ((s1.x - s2.x) * (s2.y - e2.y) - (s1.y - s2.y) * (s2.x - e2.x)) /
((s1.x - e1.x) * (s2.y - e2.y) - (s1.y - e1.y) * (s2.x - e2.x));
} else if (!onPlane(l1.a, l1.b, {0, 0, 0}, {0, 1, 0})) {
val = ((s1.x - s2.x) * (s2.z - e2.z) - (s1.z - s2.z) * (s2.x - e2.x)) /
((s1.x - e1.x) * (s2.z - e2.z) - (s1.z - e1.z) * (s2.x - e2.x));
} else {
val = ((s1.y - s2.y) * (s2.z - e2.z) - (s1.z - s2.z) * (s2.y - e2.y)) /
((s1.y - e1.y) * (s2.z - e2.z) - (s1.z - e1.z) * (s2.y - e2.y));
}
return {1, s1 + (e1 - s1) * val};
}
直线与平面是否相交及交点 linePlaneCross
当直线与平面平行、给定的点构不成平面时返回 \(false\) 。
测试点信息
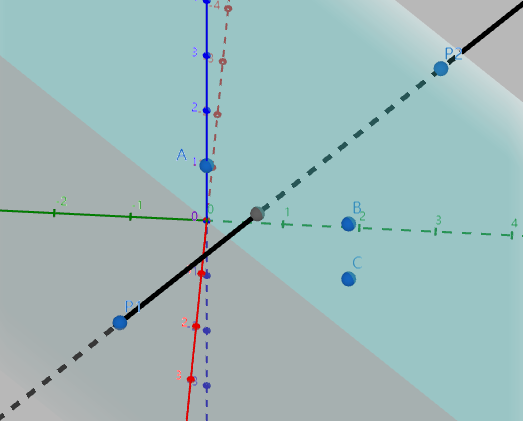
#1(正确性测试,数据集同上)
P3 A = {0, 0, 1};
P3 B = {2, 2, 2};
P3 C = {2, 2, 1};
P3 P1 = {2, -1, 0};
P3 P2 = {-1, 3, 2};
auto [a, b] = linePlaneCross({P1, P2}, {A, B, C}); // 交于 (0.7142857142857, 0.7142857142857, 0.8571428571429)
ok!
pair<bool, P3> linePlaneCross(L3 l, Plane s) {
if (linePlaneParallel(l, s)) {
return {0, {}};
}
P3 vec = getVec(s);
P3 U = vec * (s.u - l.a), V = vec * (l.b - l.a);
ld val = (U.x + U.y + U.z) / (V.x + V.y + V.z);
return {1, l.a + (l.b - l.a) * val};
}
两平面是否相交及交线 planeIntersection
当两平面平行、两平面为同一个时返回 \(false\) 。
测试点信息
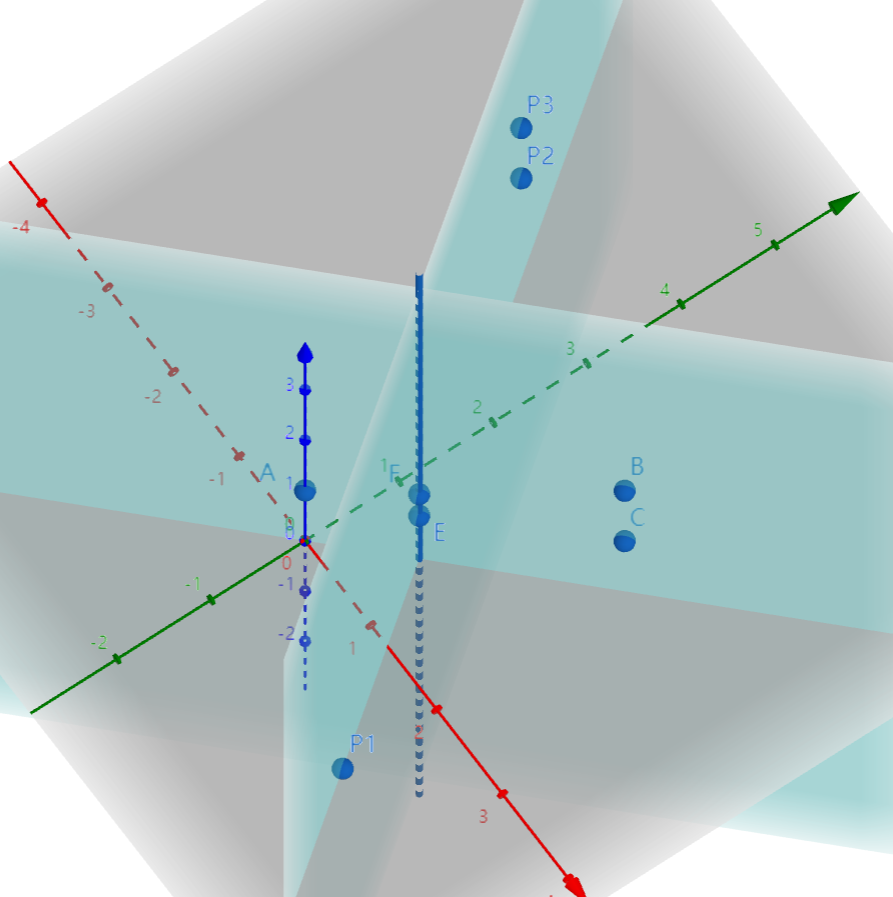
#1(正确性测试)
P3 A = {0, 0, 1};
P3 B = {2, 2, 2};
P3 C = {2, 2, 1};
P3 P1 = {2, -1, 0};
P3 P2 = {-1, 3, 2};
P3 P3 = {-1, 3, 3};
auto [a, b] = planeIntersection({A, B, C}, {P1, P2, P3});
交于点 E(0.7142857142857, 0.7142857142857, 0.8571428571429), F(0.7142857142857, 0.7142857142857, 1.2857142857143),已在上图中标出。
ok!
pair<bool, L3> planeIntersection(Plane s1, Plane s2) {
if (planeParallel(s1, s2) || same(s1, s2)) {
return {0, {}};
}
P3 U = linePlaneParallel({s2.u, s2.v}, s1) ? linePlaneCross({s2.v, s2.w}, s1).second
: linePlaneCross({s2.u, s2.v}, s1).second;
P3 V = linePlaneParallel({s2.w, s2.u}, s1) ? linePlaneCross({s2.v, s2.w}, s1).second
: linePlaneCross({s2.w, s2.u}, s1).second;
return {1, {U, V}};
}
点到直线的最近点与最近距离 pointToLine
同时返回最近点与最近距离。
测试点信息

#1(正确性测试)
P3 A = {0, 0, 1};
P3 B = {2, 2, 2};
P3 C = {0, 0, 0};
auto a = pointToLine(C, {A, B});
交于点 H(-0.2222222222222, -0.2222222222222, 0.8888888888889),已在上图中标出。最近距离为0.9428090415821。
ok!
pair<ld, P3> pointToLine(P3 p, L3 l) {
ld val = cross(p - l.a, l.a - l.b) / dis(l.a, l.b); // 面积除以底边长
ld val1 = dot(p - l.a, l.a - l.b) / dis(l.a, l.b);
return {val, l.a + val1 * standardize(l.a - l.b)};
}
点到平面的最近点与最近距离 pointToPlane
同时返回最近点与最近距离。
测试点信息
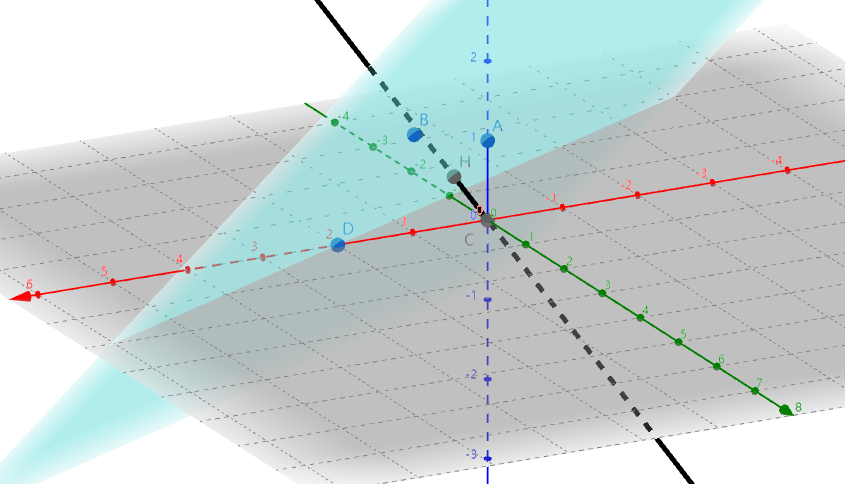
#1(正确性测试)
P3 A = {0, 0, 1};
P3 B = {2, 2, 2};
P3 C = {0, 0, 0};
P3 D = {2, 0, 0};
auto [a, b] = pointToPlane(C, {A, B, D});
交于点 H(0.2222222222222, -0.4444444444444, 0.4444444444444),已在上图中标出。最近距离为 0.6666666666667。
ok!
pair<ld, P3> pointToPlane(P3 p, Plane s) {
P3 vec = getVec(s);
ld val = dot(vec, p - s.u);
val = abs(val) / len(vec); // 面积除以底边长
return {val, p - val * standardize(vec)};
}
空间两直线的最近距离与最近点对
测试点信息
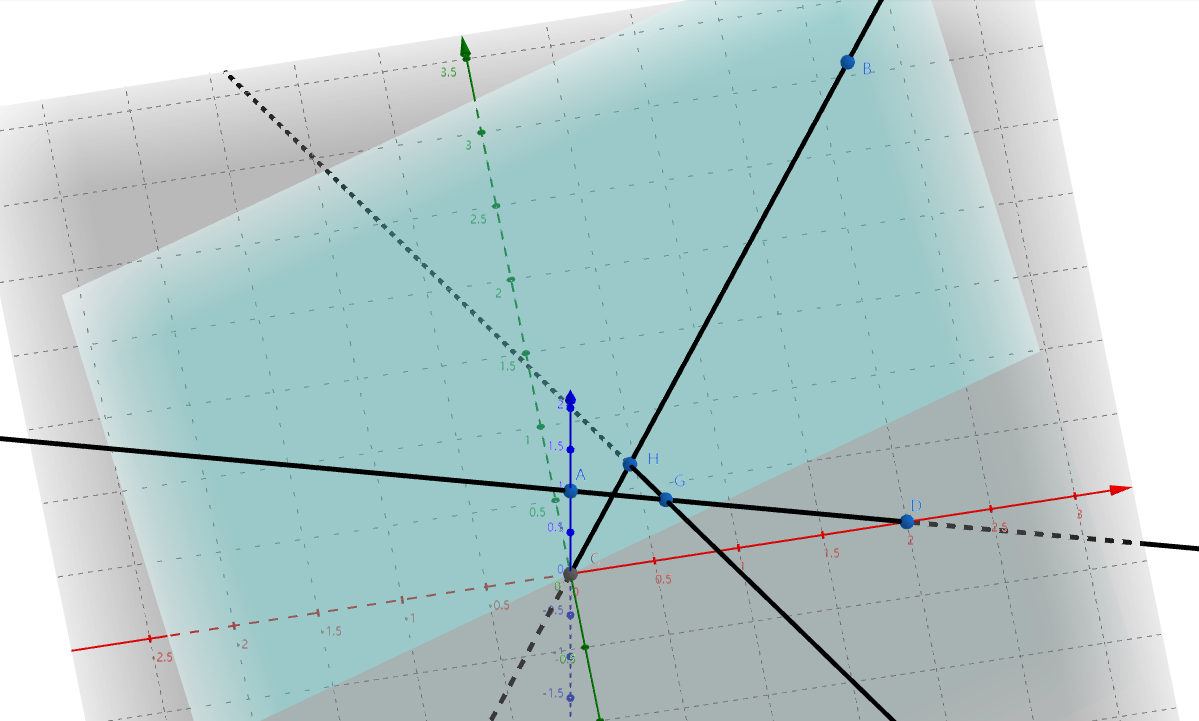
#1(正确性测试)
P3 A = {0, 0, 1};
P3 B = {2, 2, 2};
P3 C = {0, 0, 0};
P3 D = {2, 0, 0};
auto [a, b, c] = lineToLine({A, D}, {B, C});
交于点 H(0.4285714285714, 0.4285714285714, 0.4285714285714) 和 G(0.5714285714286, 0.0000000000000, 0.7142857142857),已在上图中标出。最近距离为 0.5345224838248。
ok!
tuple<ld, P3, P3> lineToLine(L3 l1, L3 l2) {
P3 vec = crossEx(l1.a - l1.b, l2.a - l2.b); // 计算同时垂直于两直线的向量
ld val = abs(dot(l1.a - l2.a, vec)) / len(vec);
P3 U = l1.b - l1.a, V = l2.b - l2.a;
vec = crossEx(U, V);
ld p = dot(vec, vec);
ld t1 = dot(crossEx(l2.a - l1.a, V), vec) / p;
ld t2 = dot(crossEx(l2.a - l1.a, U), vec) / p;
return {val, l1.a + (l1.b - l1.a) * t1, l2.a + (l2.b - l2.a) * t2};
}
三维角度与弧度
空间两直线夹角的 cos 值
任意位置的空间两直线。
ld lineCos(L3 l1, L3 l2) {
return dot(l1.a - l1.b, l2.a - l2.b) / len(l1.a - l1.b) / len(l2.a - l2.b);
}
空间两平面夹角的 cos 值
ld planeCos(Plane s1, Plane s2) {
P3 U = getVec(s1), V = getVec(s2);
return dot(U, V) / len(U) / len(V);
}
直线与平面夹角的 sin 值
ld linePlaneSin(L3 l, Plane s) {
P3 vec = getVec(s);
return dot(l.a - l.b, vec) / len(l.a - l.b) / len(vec);
}
空间多边形
正N棱锥体积公式
棱锥通用体积公式 \(V=\dfrac{1}{3}Sh\) ,当其恰好是棱长为 \(l\) 的正 \(n\) 棱锥时,有公式 \(\displaystyle V=\frac{l^3\cdot n}{12\tan \frac{\pi}{n}}\cdot\sqrt{1-\frac{1}{4\cdot \sin^2\frac{\pi}{n}}}\)。
ld V(ld l, int n) { // 正n棱锥体积公式
return l * l * l * n / (12 * tan(PI / n)) * sqrt(1 - 1 / (4 * sin(PI / n) * sin(PI / n)));
}
四面体体积
ld V(P3 a, P3 b, P3 c, P3 d) {
return abs(dot(d - a, crossEx(b - a, c - a))) / 6;
}
点是否在空间三角形上
点位于边界上时返回 \(false\) 。
bool pointOnTriangle(P3 p, P3 p1, P3 p2, P3 p3) {
return pointOnSegmentSide(p, p1, {p2, p3}) && pointOnSegmentSide(p, p2, {p1, p3}) &&
pointOnSegmentSide(p, p3, {p1, p2});
}
线段是否与空间三角形相交及交点
只有交点在空间三角形内部时才视作相交。
pair<bool, P3> segmentOnTriangle(P3 l, P3 r, P3 p1, P3 p2, P3 p3) {
P3 x = crossEx(p2 - p1, p3 - p1);
if (sign(dot(x, r - l)) == 0) {
return {0, {}};
}
ld t = dot(x, p1 - l) / dot(x, r - l);
if (t < 0 || t - 1 > 0) { // 不在线段上
return {0, {}};
}
bool type = pointOnTriangle(l + (r - l) * t, p1, p2, p3);
if (type) {
return {1, l + (r - l) * t};
} else {
return {0, {}};
}
}
空间三角形是否相交
相交线段在空间三角形内部时才视作相交。
bool triangleIntersection(vector<P3> a, vector<P3> b) {
for (int i = 0; i < 3; i++) {
if (segmentOnTriangle(b[i], b[(i + 1) % 3], a[0], a[1], a[2]).first) {
return 1;
}
if (segmentOnTriangle(a[i], a[(i + 1) % 3], b[0], b[1], b[2]).first) {
return 1;
}
}
return 0;
}
常用例题
将平面某点旋转任意角度
题意:给定平面上一点 \((a,b)\) ,输出将其逆时针旋转 \(d\) 度之后的坐标。例题。
signed main() {
int a, b, d;
cin >> a >> b >> d;
ld l = hypot(a, b); // 库函数,求直角三角形的斜边
ld alpha = atan2(b, a) + toArc(d);
cout << l * cos(alpha) << " " << l * sin(alpha) << endl;
}
平面最近点对(set解)
借助 set ,在严格 \(\mathcal O(N\log N)\) 复杂度内求解,比常见的分治法稍快。模板1:洛谷基础题,模板2:洛谷数据加强版,模板3:洛谷数据加强加强版,例题。
template<class T> T sqr(T x) {
return x * x;
}
using V = Point<int>;
signed main() {
int n;
cin >> n;
vector<V> in(n);
for (auto &it : in) {
cin >> it;
}
int dis = disEx(in[0], in[1]); // 设定阈值
sort(in.begin(), in.end());
set<V> S;
for (int i = 0, h = 0; i < n; i++) {
V now = {in[i].y, in[i].x};
while (dis && dis <= sqr(in[i].x - in[h].x)) { // 删除超过阈值的点
S.erase({in[h].y, in[h].x});
h++;
}
auto it = S.lower_bound(now);
for (auto k = it; k != S.end() && sqr(k->x - now.x) < dis; k++) {
dis = min(dis, disEx(*k, now));
}
if (it != S.begin()) {
for (auto k = prev(it); sqr(k->x - now.x) < dis; k--) {
dis = min(dis, disEx(*k, now));
if (k == S.begin()) break;
}
}
S.insert(now);
}
cout << sqrt(dis) << endl;
}
平面若干点能构成的最大四边形的面积(简单版,暴力枚举)
题意:平面上存在若干个点,保证没有两点重合、没有三点共线,你需要从中选出四个点,使得它们构成的四边形面积是最大的,注意这里能组成的四边形可以不是凸四边形。例题。
暴力枚举其中一条对角线后枚举剩余两个点,\(\mathcal O(N^3)\) 。
signed main() {
int n;
cin >> n;
vector<Pi> in(n);
for (auto &it : in) {
cin >> it;
}
ld ans = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) { // 枚举对角线
ld l = 0, r = 0;
for (int k = 0; k < n; k++) { // 枚举第三点
if (k == i || k == j) continue;
if (pointOnLineLeft(in[k], {in[i], in[j]})) {
l = max(l, triangleS(in[k], in[j], in[i]));
} else {
r = max(r, triangleS(in[k], in[j], in[i]));
}
}
if (l * r != 0) { // 确保构成的是四边形
ans = max(ans, l + r);
}
}
}
cout << ans << endl;
}
平面若干点能构成的最大四边形的面积(困难版,分类讨论+旋转卡壳)
题意:平面上存在若干个点,可能存在多点重合、共线的情况,你需要从中选出四个点,使得它们构成的四边形面积是最大的,注意这里能组成的四边形可以不是凸四边形、可以是退化的四边形。例题。
当凸包大小 \(\le 2\) 时,说明是退化的四边形,答案直接为 \(0\) ;大小恰好为 \(3\) 时,说明是凹四边形,我们枚举不在凸包上的那一点,将两个三角形面积相减既可得到答案;大小恰好为 \(4\) 时,说明是凸四边形,使用旋转卡壳求解。
using V = Point<int>;
signed main() {
int Task = 1;
for (cin >> Task; Task; Task--) {
int n;
cin >> n;
vector<V> in_(n);
for (auto &it : in_) {
cin >> it;
}
auto in = staticConvexHull(in_, 0);
n = in.size();
int ans = 0;
if (n > 3) {
ans = rotatingCalipers(in);
} else if (n == 3) {
int area = triangleAreaEx(in[0], in[1], in[2]);
for (auto it : in_) {
if (it == in[0] || it == in[1] || it == in[2]) continue;
int Min = min({triangleAreaEx(it, in[0], in[1]), triangleAreaEx(it, in[0], in[2]), triangleAreaEx(it, in[1], in[2])});
ans = max(ans, area - Min);
}
}
cout << ans / 2;
if (ans % 2) {
cout << ".5";
}
cout << endl;
}
}
线段将多边形切割为几个部分
题意:给定平面上一线段与一个任意多边形,求解线段将多边形切割为几个部分;保证线段的端点不在多边形内、多边形边上,多边形顶点不位于线段上,多边形的边不与线段重叠;多边形端点按逆时针顺序给出。下方的几个样例均合法,答案均为 \(3\) 。例题。
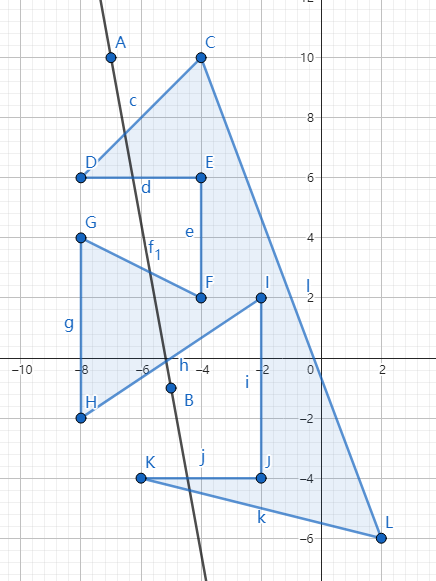
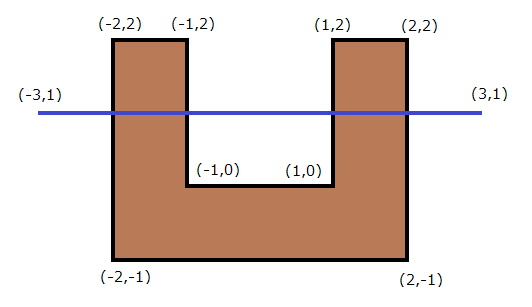
当线段切割多边形时,本质是与多边形的边交于两个点、或者说是与多边形的两条边相交,设交点数目为 \(x\) ,那么答案即为 \(\frac{x}{2}+1\) 。于是,我们只需要计算交点数量即可,先判断某一条边是否与线段相交,再判断边的两个端点是否位于线段两侧。
signed main() {
Pi s, e;
cin >> s >> e; // 读入线段
int n;
cin >> n;
vector<Pi> in(n);
for (auto &it : in) {
cin >> it; // 读入多边形端点
}
int cnt = 0;
for (int i = 0; i < n; i++) {
Pi x = in[i], y = in[(i + 1) % n];
cnt += (pointNotOnLineSide(x, y, {s, e}) && segmentIntersection(Line{x, y}, {s, e}));
}
cout << cnt / 2 + 1 << endl;
}
平面若干点能否构成凸包(暴力枚举)
题意:给定平面上若干个点,判断其是否构成凸包。例题。
可以直接使用凸包模板,但是代码较长;在这里我们使用暴力枚举试点,也能以 \(\mathcal O(N)\) 的复杂度通过。当两个向量的叉乘 \(\le0\) 时说明其夹角大于等于 \(180\degree\) ,使用这一点即可判定。
signed main() {
int n;
cin >> n;
vector<Point<ld>> in(n);
for (auto &it : in) {
cin >> it;
}
for (int i = 0; i < n; i++) {
auto A = in[(i - 1 + n) % n];
auto B = in[i];
auto C = in[(i + 1) % n];
if (cross(A - B, C - B) > 0) {
cout << "No\n";
return 0;
}
}
cout << "Yes\n";
}
凸包上的点能构成的最大三角形(暴力枚举)
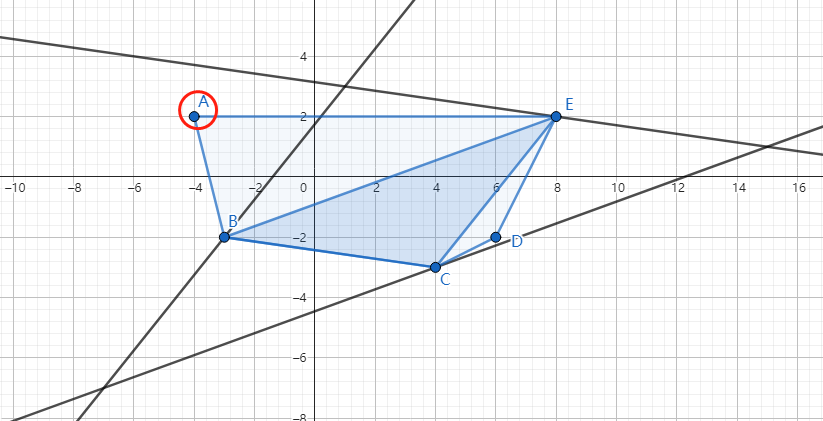
可以直接使用凸包模板,但是代码较长;在这里我们使用暴力枚举试点,也能以 \(\mathcal O(N)\) 的复杂度通过。例题。
另外补充一点性质:所求三角形的反互补三角形一定包含了凸包上的所有点(可以在边界)。通俗的说,构成的三角形是这个反互补三角形的中点三角形。如下图所示,点 \(A\) 不在 \(\triangle BCE\) 的反互补三角形内部,故 \(\triangle BCE\) 不是最大三角形;\(\triangle ACE\) 才是。
signed main() {
int n;
cin >> n;
vector<Point<int>> in(n);
for (auto &it : in) {
cin >> it;
}
#define S(x, y, z) triangleAreaEx(in[x], in[y], in[z])
int i = 0, j = 1, k = 2;
while (true) {
int val = S(i, j, k);
if (S((i + 1) % n, j, k) > val) {
i = (i + 1) % n;
} else if (S((i - 1 + n) % n, j, k) > val) {
i = (i - 1 + n) % n;
} else if (S(i, (j + 1) % n, k) > val) {
j = (j + 1) % n;
} else if (S(i, (j - 1 + n) % n, k) > val) {
j = (j - 1 + n) % n;
} else if (S(i, j, (k + 1) % n) > val) {
k = (k + 1) % n;
} else if (S(i, j, (k - 1 + n) % n) > val) {
k = (k - 1 + n) % n;
} else {
break;
}
}
cout << i + 1 << " " << j + 1 << " " << k + 1 << endl;
}
凸包上的点能构成的最大四角形的面积(旋转卡壳)
由于是凸包上的点,所以保证了四边形一定是凸四边形,时间复杂度 \(\mathcal O(N^2)\) 。
template<class T> T rotatingCalipers(vector<Point<T>> &p) {
#define S(x, y, z) triangleAreaEx(p[x], p[y], p[z])
int n = p.size();
T ans = 0;
auto nxt = [&](int i) -> int {
return i == n - 1 ? 0 : i + 1;
};
for (int i = 0; i < n; i++) {
int p1 = nxt(i), p2 = nxt(nxt(nxt(i)));
for (int j = nxt(nxt(i)); nxt(j) != i; j = nxt(j)) {
while (nxt(p1) != j && S(i, j, nxt(p1)) > S(i, j, p1)) {
p1 = nxt(p1);
}
if (p2 == j) {
p2 = nxt(p2);
}
while (nxt(p2) != i && S(i, j, nxt(p2)) > S(i, j, p2)) {
p2 = nxt(p2);
}
ans = max(ans, S(i, j, p1) + S(i, j, p2));
}
}
return ans;
#undef S
}
判断一个凸包是否完全在另一个凸包内
题意:给定一个凸多边形 \(A\) 和一个凸多边形 \(B\) ,询问 \(B\) 是否被 \(A\) 包含,分别判断严格/不严格包含。例题。
考虑严格包含,使用 \(A\) 点集计算出凸包 \(T_1\) ,使用 \(A,B\) 两个点集计算出不严格凸包 \(T_2\) ,如果包含,那么 \(T_1\) 应该与 \(T_2\) 完全相等;考虑不严格包含,在计算凸包 \(T_2\) 时严格即可。最终以 \(\mathcal O(N)\) 复杂度求解,且代码不算很长。
常用结论
平面几何结论归档
-
hypot函数可以直接计算直角三角形的斜边长; -
边心距是指正多边形的外接圆圆心到正多边形某一边的距离,边长为 \(s\) 的正 \(n\) 角形的边心距公式为 \(\displaystyle a=\frac{t}{2\cdot\tan \frac{\pi}{n}}\) ,外接圆半径为 \(R\) 的正 \(n\) 角形的边心距公式为 \(a=R\cdot \cos \dfrac{\pi}{n}\) ;
-
三角形外接圆半径为 \(\dfrac{a}{2\sin A}=\dfrac{abc}{4S}\) ,其中 \(S\) 为三角形面积,内切圆半径为 \(\dfrac{2S}{a+b+c}\);
-
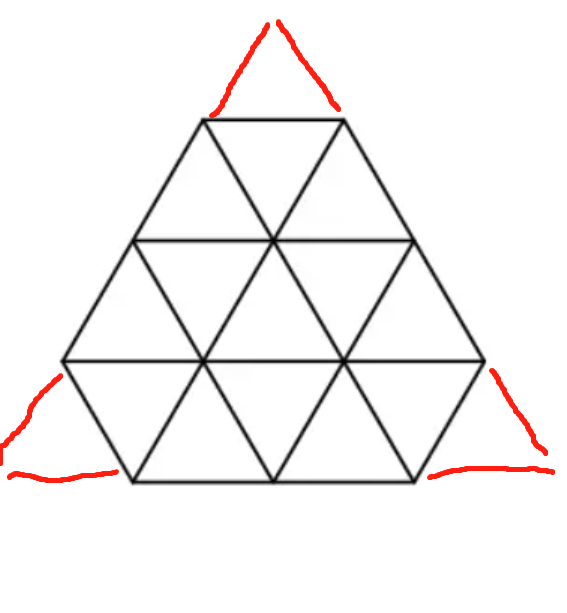
由小正三角形拼成的大正三角形,耗费的小三角形数量即为构成一条边的小三角形数量的平方。如下图,总数量即为 \(4^2\) See。
-
正 \(n\) 边形圆心角为 \(\dfrac{360^{\circ}}{n}\) ,圆周角为 \(\dfrac{180^{\circ}}{n}\) 。定义正 \(n\) 边形上的三个顶点 \(A,B\) 和 \(C\)(可以不相邻),使得 \(\angle ABC=\theta\) ,当 \(n\le 360\) 时,\(\theta\) 可以取 \(1^{\circ}\) 到 \(179^{\circ}\) 间的任何一个整数 See。
-
某一点 \(B\) 到直线 \(AC\) 的距离公式为 \(\dfrac{|\vec{BA}\times \vec{BC}|}{|AC|}\) ,等价于 \(\dfrac{|aX+bY+c|}{\sqrt{a^2+b^2}}\)。
-
atan(y / x)函数仅用于计算第一、四象限的值,而atan2(y, x)则允许计算所有四个象限的正反切,在使用这个函数时,需要尽量保证 \(x\) 和 \(y\) 的类型为整数型,如果使用浮点数,实测会慢十倍。 -
在平面上有奇数个点 \(A_0,A_1,\dots,A_n\) 以及一个点 \(X_0\) ,构造 \(X_1\) 使得 \(X_0,X_1\) 关于 \(A_0\) 对称、构造 \(X_2\) 使得 \(X_1,X_2\) 关于 \(A_1\) 对称、……、构造 \(X_j\) 使得 \(X_{j-1},X_j\) 关于 \(A_{(j-1)\mod n}\) 对称。那么周期为 \(2n\) ,即 \(A_0\) 与 \(A_{2n}\) 共点、\(A_1\) 与 \(A_{2n+1}\) 共点 See 。
-
已知 \(A\ (x_A, y_A)\) 和 \(X\ (x_X,y_X)\) 两点及这两点的坐标,构造 \(Y\) 使得 \(X,Y\) 关于 \(A\) 对称,那么 \(Y\) 的坐标为 \((2\cdot x_A-x_X,2\cdot y_A-y_X)\) 。
-
海伦公式:已知三角形三边长 \(a,b\) 和 \(c\) ,定义 \(p=\dfrac{a+b+c}{2}\) ,则 \(S_{\triangle}=\sqrt{p(p-a)(p-b)(p-c)}\) ,在使用时需要注意越界问题,本质是铅锤定理,一般多使用叉乘计算三角形面积而不使用该公式。
-
棱台体积 \(V=\frac{1}{3}(S_1+S_2+\sqrt{S_1S_2})\cdot h\),其中 \(S_1,S_2\) 为上下底面积。
-
正棱台侧面积 \(\frac{1}{2}(C_1+C_2)\cdot L\),其中 \(C_1,C_2\) 为上下底周长,\(L\) 为斜高(上下底对应的平行边的距离)。
-
球面积 \(4\pi r^2\),体积 \(\frac{4}{3}\pi r^3\)。
-
正三角形面积 \(\dfrac{\sqrt 3 a^2}{4}\),正四面体面积 \(\dfrac{\sqrt 2 a^3}{12}\)。
-
设扇形对应的圆心角弧度为 \(\theta\) ,则面积为 \(S=\frac{\theta}{2}\cdot R^2\) 。
立体几何结论归档
- 已知向量 \(\vec{r}=\{x,y,z\}\) ,则该向量的三个方向余弦为 \(\cos \alpha =\dfrac{x}{|\vec r|}=\dfrac{x}{\sqrt{x^2+y^2+z^2}}; \ \cos \beta = \dfrac{y}{|\vec r|};\ \cos \gamma =\dfrac{z}{|\vec r|}\) 。其中 \(\alpha,\beta,\gamma\in [0,\pi]\) ,\(\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1\) 。
本文参考列表
【HIT】计算几何模板.pdf
codeforces:jiangly 的计算几何模板合集
codeforces:Hydrogen_zyx 的计算几何模板合集
codeforces:tonegawa 的计算几何模板合集
稀土掘金:苹果API搬运工 的 Swift 版 3D 计算几何教程
博客园:我在努力。。。 的计算几何模板合集
QQ群 菜菜园子各位前辈提供的资料整理



 浙公网安备 33010602011771号
浙公网安备 33010602011771号