2022 浙江省赛(参赛队)
比赛相关信息
比赛信息
比赛名称: 2022年第19届浙江省省赛 - The 19th Zhejiang Provincial Collegiate Programming Contest
比赛地址: CodeForces
榜单回顾: Board全部参赛队伍: 排名至426
金:
银:
铜:
比赛过程回顾
| A | B | C | D | E | F | G | H | I | J | K | L | M | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 错误次数 | 1 | 0 | 0 | 2 | 1 | 1 | 4 | ||||||
| 首次提交时间 | 0:20:45 | 0:08:07 | 0:11:17 | 1:54:15 | 3:32:07 | 0:38:32 | 3:00:36 | ||||||
| 首A时间 | 0:27:43 | 0:08:07 | 0:11:17 | 2:18:18 | 4:32:41 | 0:38:32 | 4:57:46 | ||||||
| 状态 | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||
| 知识点 |
共 7 题,951m,Rk 112。
✔:比赛时通过;⚪:比赛时尝试过;补:已补题。
部分题解与小结
A - JB Loves Math
小评
\(\mathcal{Consider\ by\ Wcj\ \&\ Hamine}\),\(\mathcal{Solved\ by\ Wcj}\) 。
打卡题(1/4)。
第一道开的题目,在发现错误率极高后果断先做了另外的题。错误率高的原因在于题目意义表达的不是很清晰(赛时并未明确 \(x,y\) 的取值能否变化,但是补题题集中加上了),在交了一发WA之后才意识到 \(x,y\) 的取值一旦固定便不能改变,修改了分类讨论后得解。
思路
答案不超过 \(3\) ,分类讨论即可。
- \(b=a\) ,出 \(0\) ;
- \(b>a\)
- \(b-a\) 为奇数,出 \(1\) ;
- \(b-a\) 为偶数
- \(\lfloor \frac{b-a}{2} \rfloor\) 为奇数时,出 \(2\) ;
- \(\lfloor \frac{b-a}{2} \rfloor\) 为偶数时,出 \(3\) ;
- \(b<a\)
- \(b-a\) 为奇数,出 \(2\) ;
- \(b-a\) 为偶数,出 \(1\) ;
B - JB Loves Comma
小评
\(\mathcal{Consider\ by\ Wcj}\),\(\mathcal{Solved\ by\ Wida}\) 。
打卡题(2/4)。
C - JB Wants to Earn Big Money
小评
\(\mathcal{Consider\ by\ Hamine}\),\(\mathcal{Solved\ by\ Hamine}\) 。
打卡题(3/4)。
G - Easy Glide
小评
\(\mathcal{Consider\ by\ Wida}\),\(\mathcal{Solved\ by\ Wida}\) 。
基础图论题,思路很简单,但是代码难度很高。
题意
给出一个二维的地图,你需要操纵一个移速为 \(V_1\) 的机器人以最短的时间从起点 \(S\) 到达终点 \(T\) 。除上述信息之外,地图上还散落着 \(N(1\le N \le 10^3)\) 个加速点,每个加速点都可以在 \(3\) 秒内让你的速度变为 \(V_2(V_2>V_1)\) ,时间不叠加。
给出起点终点 \(S,T\) 及每一个加速点的坐标,输出到达终点的最少时间。
思路
由 \(N\) 的范围,显然本题至少是 \(\mathcal O (N^2)\) 的复杂度,暴力建双向边,并计算出每一条边需要花费的时间。本题即转化为求解从 \(S\) 到 \(T\) 的最短路,跑一遍堆优化版的 \(\tt djikstra\) 即可。
需要留意的地方是,\(S,T\) 不是加速点,故建边求权值时需要特别考虑。
AC代码
点击查看代码
#define int LL
const int N = 1e6 + 7;
int n, x[N], y[N], v1, v2;
double clac(int i, int j) {
int X1 = x[i], X2 = x[j], Y1 = y[i], Y2 = y[j];
double p = (X1 - X2) * (X1 - X2);
double q = (Y1 - Y2) * (Y1 - Y2);
double len = sqrt(p + q);
if (i == 0 || i == n + 1) return len / v1;
if (3.0 * v2 >= len) return len / v2;
return 3.0 + (len - 3.0 * v2) / v1;
}
int ver[2 * N], h[2 * N], ne[2 * N], tot; double edge[2 * N];
void add(int x, int y, double w) {
ver[++ tot] = y, ne[tot] = h[x], h[x] = tot;
edge[tot] = w;
}
int v[N]; double d[N];
void dji() {
priority_queue<PII, vector<PII>, greater<PII> > q; q.push({0, 0});
memset(d, 0x7f, sizeof d); d[0] = 0;
while (!q.empty()) {
int x = q.top().second; q.pop();
if (v[x]) continue; v[x] = 1;
for (int i = h[x]; i; i = ne[i]) {
int y = ver[i];
if (d[y] > d[x] + edge[i]) {
d[y] = d[x] + edge[i];
q.push({d[y], y});
}
}
}
}
void Solve() {
cin >> n;
for (int i = 1; i <= n; ++ i) cin >> x[i] >> y[i];
cin >> x[0] >> y[0] >> x[n + 1] >> y[n + 1] >> v1 >> v2;
for (int i = 0; i <= n + 1; ++ i) {
for (int j = 0; j <= n + 1; ++ j) {
add(i, j, clac(i, j));
}
}
dji();
cout << d[n + 1] << endl;
}
signed main() {
cout << fixed << setprecision(12);
ios::sync_with_stdio(0); cin.tie(0);
Solve();
return 0;
}
I - Barbecue
小评
\(\mathcal{Consider\ by\ Wida}\),\(\mathcal{Solved\ by\ Wida\ \&\ Hamine}\) 。
非常有意思的一道题,这题能做出来真的能够说明队伍在多个知识面上均有所涉猎。
刚拿到手的时候以为这是道纯博弈,思考过后发现这道题的核心在于字符串的处理,博弈只是外包的一部分。
题意
给出一个长度为 \(N\) 的序列 \(S\) ,随后给出 \(Q\) 次询问,每次询问都会给出 \(l,r\) ,代表取出 \(S\) 的子串 \(S'\) 。对于这个子串 \(S'\) 进行操作,规定如下:
- 每一回合,拿到子串的选手需要丢弃这个子串的第一个或者最后一个字母,随后将操作后的子串交给下一个选手;
- 当子串为回文时,拥有这个子串的选手输掉了比赛;
双方均采取最优策略,对于每一个询问,输出胜者。
思路
首先考虑博弈部分,归纳后只存在两种情况:
- 先手到手时已经是回文串,则后手胜,这是显然的;
- 先手到手时不是回文串,则胜负仅与字符数量有关,下面我们尝试证明这一点。
我们假设回文部分用 \(XXX\dots XXX\) 表示,其余字母用 \(OOOO\) 表示。
当回文部分左右均存在 \(O\) 时(如 \(OOXXX\dots XXXOOO\) ),双方一定会尝试将字符串拆成只有一侧存在 \(O\) 的情况(如 \(OXXX\dots XXX\) ),而此时,拿到这个字符串的选手一定存在破局方式——将回文串拆掉(如 \(OXXX\dots XX\bar X\) ,将 \(X\) 拆除,那么即使是最坏情况下,新的字符串会变为 \(OOXX\dots XX\) ,而更一般的情况则会出现更多的 \(O\) ),那么双方依旧可以继续下去,直到字符串耗尽。
这时,这道题只需要进行回文串的判断就可以了,稍加思考后我们发现使用 \(\tt Manacher\) 算法 \(\mathcal O(n)\) 的复杂度可以通过,故直接接入即可——每次判断,以给定区域中央的字符为中心,最大的回文串长度是否超过了给定长度。
AC代码
点击查看代码
#define LL long long
const int N = 2e6 + 10;
char s[N << 1];
int p[N << 1];
int n, q; string ss;
void manacher(){
s[0] = '-', s[1] = '#';
for (int i = 0; i < n; i ++ ){
s[2 * i + 2] = ss[i];
s[2 * i + 3] = '#';
}
n = n * 2 + 1;
s[n + 1] = '+';
int mid = 0, r = 0;
for (int i = 1; i < n; i ++ ){
if (i < r) p[i] = min(p[(mid << 1) - i], r - i);
else p[i] = 1;
while(s[i - p[i]] == s[i + p[i]]) p[i]++;
if (i + p[i] > r){
r = i + p[i];
mid = i;
}
}
}
int main() {
ios::sync_with_stdio(false); cin.tie(0);
cin >> n >> q >> ss;
manacher();
for (int i = 1; i <= q; ++ i) {
int x, y;
cin >> x >> y;
int xx = x, yy = y;
x *= 2, y *= 2;
int mid = (x + y) / 2;
if ( 2 * p[mid] - 1 >= y - x + 1) cout << "Budada\n";
else {
if ((yy - xx + 1) % 2 == 0) cout << "Budada\n";
else cout << "Putata\n";
}
}
return 0;
}
L - Candy Machine
小评
\(\mathcal{Consider\ by\ Wida\ \&\ Wcj}\),\(\mathcal{Solved\ by\ Wida}\) 。
打卡题(4/4)。
题意
给出 \(N\) 颗糖果以及每一颗的甜度,你可以选择任意数量的糖果,假设你所选糖果的平均甜度为 \(\bar X\) ,那么,你将得到甜度 \(> \bar X\) 的糖果。如何选择糖果,使得你能得到的数量最多。
思路
二分,得解。
AC代码
点击查看代码
#define int LL
const int N = 1e6 + 7;
int a[N], add, ans;
double avg;
void Solve() {
int n; cin >> n;
FOR (i, 1, n) cin >> a[i], add += a[i];
sort(a + 1, a + 1 + n);
FOR (i, 0, n) {
add -= a[n - i + 1];
avg = add / (n - i + 0.0);
int x = upper_bound(a + 1, a + 1 + n - i, avg) - a;
cmax(ans, n - i - x + 1);
}
cout << ans << endl;
}
M - BpbBppbpBB
小评
\(\mathcal{Consider\ by\ \pmb{Hamine} \ \&\ \pmb{Wida}\ \&\ \pmb{Wcj}}\),\(\mathcal{Solved\ by\ \pmb{Hamine}}\) 。
非常有意思的一道题。
赛时一致认为是大模拟题,来回的调错,前前后后花了三个小时有余,才最终得解。赛后得知是数论题的我们三直接尬住了……
题意
给定了两种印章的形状,如下图所示。
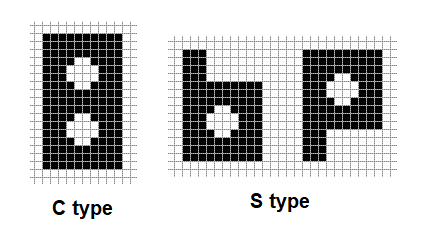
现在,使用上图两种印章,在一张方格纸上进行了若干次拓印(可能存在旋转),保证拓印彼此不重叠,保证拓印完整。询问分别进行了几次拓印。
思路
赛后正解(数论)
假设两种印章分别使用了 \(x,y\) 次,根据黑点、洞的数量我们可以得到两个方程,联立即得解。
现在问题在于如何求解洞的数量,由于印章最短边长度为 \(3\) ,而洞的最长边长度为 \(2\) ,故对于遇到的每一个白点,我们只需要按下图模拟验证即可判定其是否为洞。
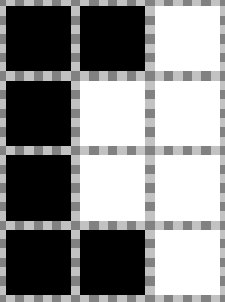
AC代码
点击查看代码
#define int LL
int sum, cnt;
char c[1026][1026];
int m_i[] = {
0, 0,
1, 1, 1,
2, 2, 2,
3, 3
}, m_j[] = {
0, 1,
-1, 0, 1,
-1, 0, 1,
0, 1
}, M_i[] = {0,
0, 0,
1,
2,
3, 3,
}, M_j[] = {0,
-2, -1,
-2,
-2,
-2, -1,
};
void Solve() {
int n, m; cin >> n >> m;
FOR (i, 1, n) FOR (j, 1, m) {
cin >> c[i][j];
if (c[i][j] == '#') ++ sum;
}
FOR (i, 2, n - 4) FOR (j, 3, m - 3) {
if (c[i][j] == '#') continue;
int flag = 1;
FOR (t, 1, 11) {
if (c[i + m_i[t]][j + m_j[t]] == '.') ++ flag;
}
FOR (t, 1, 8) {
if (c[i + M_i[t]][j + M_j[t]] == '#') ++ flag;
}
if (flag == 20) ++ cnt;
}
int ans = (100 * cnt - sum) / 54;
cout << ans << " " << cnt - 2 * ans;
}
文 / WIDA
2022.07.03 成文
首发于WIDA个人博客,仅供学习讨论



 浙公网安备 33010602011771号
浙公网安备 33010602011771号