算法笔记——奇技淫巧
islower 返回值

需要注意的是,官方文档定义的是零和非零,而不是 \(0\) 和 \(1\) 。
LLVM 参数调整
本章节部分内容参考自网络文章1、网络文章2。LLVM是一个代码格式化工具,修改一些默认参数使之更好的符合你的代码风格,以下是我个人的调整内容。
BasedOnStyle: LLVM
IndentWidth: 4
AllowShortLoopsOnASingleLine: true
AllowShortIfStatementsOnASingleLine: true
AllowShortFunctionsOnASingleLine: Empty
NamespaceIndentation: All
ColumnLimit: 100
IndentPPDirectives: BeforeHash
SpaceAfterTemplateKeyword: false
MaxEmptyLinesToKeep: 2
ReflowComments: true
AlignTrailingComments: false
AllowShortLoopsOnASingleLine: true 允许合并短的循环到单行上:可以让没有括号单独一行的短语句合并到上一行的结尾。
// 格式化前
void solve() {
while (1)
continue;
}
// 格式化后
void solve() {
while (1) continue;
}
AllowShortIfStatementsOnASingleLine : true 允许合并短的if语句到单行上:同上,注意带 else 或 else if 后不生效。
AllowShortFunctionsOnASingleLine: Empty 仅允许合并短的空函数到单行上。
NamespaceIndentation : All 缩进全部的命名空间。
ColumnLimit : 100 列数限制,列数超过这个值的行会被自动换行。
IndentPPDirectives : BeforeHash 对 define 语句缩进。
// 设置为None时
#ifndef ONLINE_JUDGE
#define tout cout
#include <bits/wida.h>
#endif
// 设置为AfterHash时
#ifndef ONLINE_JUDGE
# define tout cout
# include <bits/wida.h>
#endif
// 设置为BeforeHash时
#ifndef ONLINE_JUDGE
#define tout cout
#include <bits/wida.h>
#endif
SpaceAfterTemplateKeyword: false 不在可变模板关键字 template 后插入空格。
// 不设置时
template <class T> void chk(T x) {}
// 设置为false时
template<class T> void chk(T x) {}
MaxEmptyLinesToKeep: 2 设置最大持续空行:如果有非常多空行,会被自动删除到剩两行。
ReflowComments : true 会对列数超过 ColumnLimit 设置的注释进行自动换行。
// 格式化前
// veryVeryVeryVeryVeryVeryVeryVeryVeryVeryVeryLongComment with plenty of information
/* second veryVeryVeryVeryVeryVeryVeryVeryVeryVeryVeryLongComment with plenty of information */
// 格式化后
// veryVeryVeryVeryVeryVeryVeryVeryVeryVeryVeryLongComment with plenty of
// information
/* second veryVeryVeryVeryVeryVeryVeryVeryVeryVeryVeryLongComment with plenty of
* information */
AlignTrailingComments : false 不对齐尾部注释。
// 设置为true时
int a = 0; // 初始化a
int cnt = 20; // 初始化cnt
// 设置为false时
int a = 0; // 初始化a
int cnt = 20; // 初始化cnt
namespace 与 struct 封装
namespace
使用 namespace 名作为前缀,可以十分清楚的区分工程的各个模块,允许定义相同名称的函数与变量,常见于大模拟题、大暴力题。
相似于 using namespace std ,如果不加上这一句,所有的 std 函数前都需要加上 std:: ,例如蒋老师的代码。样例如下:
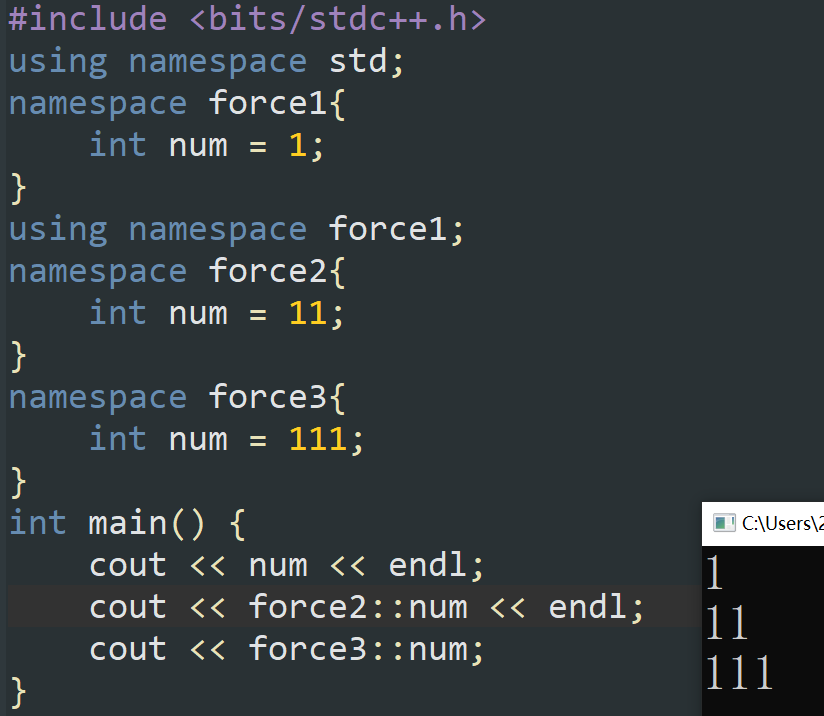
struct
相较于 namespace 封装更加灵活,可以类似的看成是一种自定义的类型,这样一来就可以产生多个互不相干的变量。
就例如并查集 DSU ,有时候一道题会需要用到多个并查集(相互独立),这个时候 namespace 就无法满足,而需要使用 struct 封装了。
个人模板详解
// 使用万能头文件简化不必要的代码,但是代价是略微增加编译时间
#include <bits/stdc++.h>
using namespace std;
// 定义一个本地宏,使得以下内容只在本地运行,而不会在OJ平台上运行,方便调试
#ifndef ONLINE_JUDGE
// 这个头文件是我自己写的,里面包含了我自己本地用的debug函数
#include <bits/wida.h>
#endif // 本地宏到此结束
// 全局宏定义,这里包含了一些个人代码习惯
#define int int64_t // 将全部int型的变量变为long long类型,避免越界
#define endl "\n" // endl会清空键盘缓冲区,导致不必要的时间浪费,而'\n'不会
void solve() { // 如果是多组测试数据,则直接写进solve函数里,方便剪枝之类的中途跳出
}
signed main() {
int Task = 1;
for (cin >> Task; Task; Task--) {
solve();
}
}
int __FAST_IO__ = []() { // 这个写法可以重构输入输出
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin); // 用于读取本地文件
freopen("out.txt", "w", stdout); // 输出至本地文件中
#endif
ios::sync_with_stdio(0), cin.tie(0);
cout.tie(0);
cout << fixed << setprecision(12);
return 0;
}();
除此之外,还有一个专门为竞赛设计的空间,里面重定义了一些可能用得到的加快码速的内容,仅供参考。
namespace WIDA {
// 常用宏定义
using PII = pair<int, int>;
using TII = tuple<int, int, int>;
#define FOR(i, a, b) for (int i = (int)(a); i <= (int)(b); i++)
#define FOR2(i, a, b) for (int i = (int)(a); i <= (int)(b); i += 2)
#define FORD(i, b, a) for (int i = (int)(a); i >= (int)(b); i--)
#define ALL(a) a.begin(), a.end()
#define RALL(a) a.rbegin(), a.rend()
#define VI vector<int>
#define RE return;
#define RET return true;
#define REF return false;
#define Yes cout << "Yes" << endl;
#define YES cout << "YES" << endl;
#define No cout << "No" << endl;
#define NO cout << "NO" << endl;
#define pb push_back
#define fi first
#define se second
#define sz size()
// 重定义输入输出
template <class... Args> void __(Args... args) { // 快速输出
auto _ = [&](auto x) { cout << x << " "; };
int arr[] = {(_(args), 0)...};
cout << "\n";
}
template <class T> istream &operator>>(istream &is, vector<T> &v) { // 直接读入vector
for (auto &x : v) is >> x;
return is;
}
template <class T, class = decay_t<decltype(*begin(declval<T>()))>,
class = enable_if_t<!is_same<T, string>::value>>
ostream &operator<<(ostream &os, const T &c) { // 直接输出容器
for (auto it = c.begin(); it != c.end(); ++it)
os << &" "[2 * (it == c.begin())] << *it;
return os;
}
// 常用库函数重定义
template <typename T> T min(const vector<T> &v) {
return *min_element(v.begin(), v.end());
}
template <typename T> T max(const vector<T> &v) {
return *max_element(v.begin(), v.end());
}
template <typename T> T acc(const vector<T> &v) {
return accumulate(v.begin(), v.end(), T(0LL));
}
template <class T> void reverse(vector<T> &v) {
reverse(v.begin(), v.end());
}
template <class T> void sort(vector<T> &v) {
sort(v.begin(), v.end());
}
template <class T> void rsort(vector<T> &v) {
sort(v.rbegin(), v.rend());
}
template <class T> T mymax(T x, T y) {
return x < y ? y : x;
}
template <class T> T mymin(T x, T y) {
return x > y ? y : x;
}
template <class T> void cmax(T &x, T y) {
x = mymax(x, y);
}
template <class T> void cmin(T &x, T y) {
x = mymin(x, y);
}
template <class T> T sign(const T &a) {
return a == 0 ? 0 : (a < 0 ? -1 : 1);
}
template <class T> T floor(const T &a, const T &b) {
T A = abs(a), B = abs(b);
assert(B != 0);
return sign(a) * sign(b) > 0 ? A / B : -(A + B - 1) / B;
}
template <class T> T ceil(const T &a, const T &b) {
T A = abs(a), B = abs(b);
assert(b != 0);
return sign(a) * sign(b) > 0 ? (A + B - 1) / B : -A / B;
}
int mypow(int n, int k, int p) {
int r = 1;
for (; k; k >>= 1, n = n * n % p) {
if (k & 1) r = r * n % p;
}
return r;
}
const int N = 1e6 + 7;
const int INF = numeric_limits<int>::max();
} // namespace WIDA
using namespace WIDA;
科学计数法 E
大于 1E16 时超过有效位,计算无效。
const int N15 = 1E15 + 1;
const int N16 = 1E16 + 1;
const int Ntt = 1E16 + 123456789;
cout << N15 << endl; // 输出 1000000000000001
cout << N16 << endl; // 输出 10000000000000000
cout << Ntt << endl; // 输出 10000000123456788
因为 E 本质是浮点数,所以可以用浮点数的知识来解释这一现象,参见下文《关于浮点数》。
编译器设置
本地扩栈
在 C++ 编译命令中加入以下内容:-Wl,--stack=268435456 。
OJ扩栈
一般的OJ都默认栈空间等于最大空间限制,但是在某些OJ(比如旧时代的杭电OJ)可能并没有这样的设定,所以需要我们手动扩栈。你需要在主函数 main 中加入以下内容:
int main() {
int size(512<<20); // 512M
__asm__ ( "movq %0, %%rsp\n"::"r"((char*)malloc(size)+size));
/*
HERE YOUR CODE
*/
exit(0);
}
需要额外注意的是,请使用 exit(0) 作为函数的结尾,否则可能出现RE。下图为某次杭电多校中官方的扩栈提示。
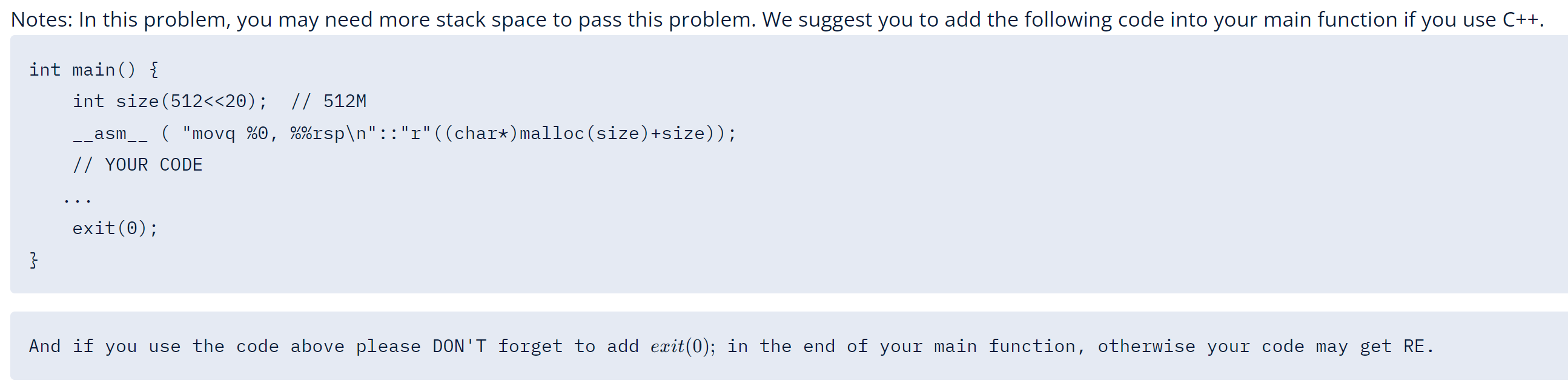
关于深度优先搜索导致的爆栈问题
某道正解是 \(\tt 0-1bfs\) 的题目,新生尝试用 \(\tt dfs\) 解决,结果没有WA而是RE了,联想到此前我也有过一道类似的题RE(正解是 \(\tt dsu\) 计算连通块数量,我使用了 \(\tt dfs\) 结果疯狂段错误),于是决定完全弄清楚这个问题,测试了很久,现在将一些结果写在这里。
首先说明结论:RE的最重要原因在于你的代码写的太复杂了,次要原因在于你运气不好。
以这个新生的情况说明为什么是代码太复杂。因为我注意到 有人是使用 \(\tt dfs\) 通过的,而这份代码有一个特点便在于其非常简洁,没有多余的无用的搜索过程;而这个新生的主体思路虽然与之类似,但是 实现的过程非常的复杂,猜想这是RE的主要原因。
以我的情况说明为什么是运气不好。经过我的测试,用 vector 一定RE、用 function 一定RE;用外置的 dfs 不RE、用 auto 代替 function 不RE。跟个人码风有极大的关系,所以直接归类为运气不好了。
附几次重要的提交记录:
使用静态数组且外置 dfs,未RE,此程序写法作为基准写法。
\([1]:\) 使用 function 替代外置 dfs,RE -> \([2]:\) 使用 auto 替代 function,未RE -> \([3]:\) 使用 vector 替代静态数组,RE。
最后的结论是:如果用DFS莫名其妙RE了那就换BFS吧。
解决编译极慢的问题
了解了下原因,发现是电脑杀毒软件的问题(在运行exe前会先扫描一遍),提供两种解决方案:
其一是没有安装任何额外的杀毒软件,参见该链接;其二是安装了额外的杀毒软件,这里以我装的火绒为例(如图,两步骤完成):
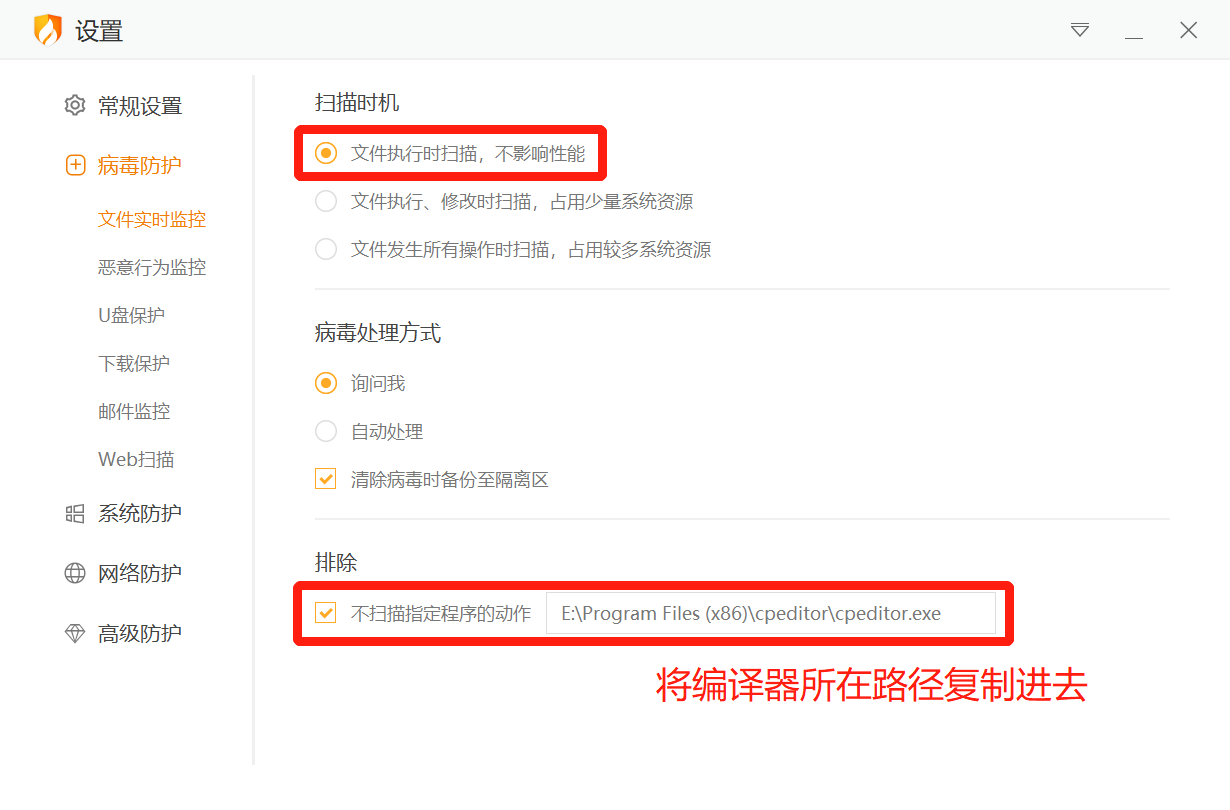
效果对比:


大整数类 __int128
只在基于 \(\tt Lumix\) 系统的环境下可用,38位精度,除输入输出外与普通数据类型无差别。
为了方便使用,我将其与快读封装在同一个命名空间里,输入输出流定义如下:
namespace QuickRead { // 读入优化封装,支持__int128
char buf[1 << 21], *p1 = buf, *p2 = buf;
inline int getc() {
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++;
}
template <typename T> void Cin(T &a) {
T ans = 0; bool f = 0; char c = getc();
for (; c < '0' || c > '9'; c = getc()) if (c == '-') f = 1;
for (; c >= '0' && c <= '9'; c = getc()) ans = ans * 10 + c - '0';
a = f ? -ans : ans;
}
template <typename T, typename... Args> void Cin(T &a, Args &...args) {
Cin(a), Cin(args...);
}
template <typename T> void write(T x) { // 注意,这里输出不带换行
if (x < 0) putchar('-'), x = -x;
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
using i128 = __int128_t;
i128 abs(const i128 &x) {
return x > 0 ? x : -x;
}
auto &operator>>(istream &it, i128 &j) {
string val; it >> val;
reverse(val.begin(), val.end());
i128 ans = 0;
bool f = 0; char c = val.back(); val.pop_back();
for (; c < '0' || c > '9'; c = val.back(), val.pop_back()) if (c == '-') f = 1;
for (; c >= '0' && c <= '9'; c = val.back(), val.pop_back()) ans = ans * 10 + c - '0';
j = f ? -ans : ans;
return it;
}
auto &operator<<(ostream &os, const i128 &j) {
string ans;
function<void(i128)> write = [&](i128 x) {
if (x < 0) ans += '-', x = -x;
if (x > 9) write(x / 10);
ans += x % 10 + '0';
};
write(j);
return os << ans;
}
} // namespace QuickRead
using namespace QuickRead;
相关例题:自测神地 - AcWing - A+B Problem,一道可以用大整数类逃课的题 - AtCoder - 250-like Number。
memset 漫谈
众所周知,memset 是通过字节赋值完成数组初始化的,故其可以不考虑类型大小,至多可以赋值到300余位,复杂度为 \(\mathcal O (n)\) 。常用的赋值如下:
| INFF | -INFF | \(\tt double\) 最大 | \(\tt double\) 最小 | |
|---|---|---|---|---|
memset 中的代码 |
0x3f | 0xbf | 0x4f | 0xcf |
| 实际值 | INFF | 小于-INFF | \(10^{75}\) | \(-10^{77}\) |
注意:在使用该函数赋予最大值时,我们只需要写 \(\tt{}0x3f\) ,不使用更大的数字原因在于可能会导致算术溢出。
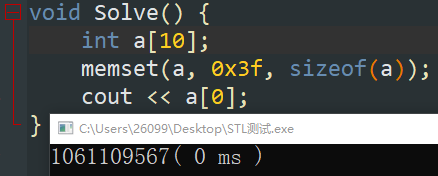
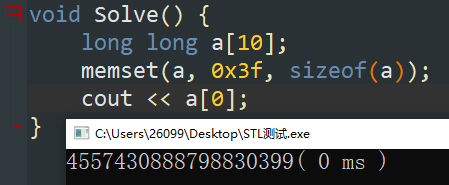
当然,对于任何类型,使用 \(\tt fill\) 函数均能够正常填充,复杂度也为 \(\mathcal O (n)\) 。
如何获取最大最小值:使用 numeric_limits 函数
这是一个一眼就看得懂的函数,你只需要在尖括号中输入想要的变量类型即可。
const int Max = numeric_limits<int>::max();
const int Min = numeric_limits<int>::min();
整除带来的取整问题
两个符号相同的数整除是向下取整,符号不同的数整除是向上取整(如 \(15\mid-2=-7\) ,相当于向上取整)。
为此,我们可以使用封装来一劳永逸的解决这一问题:
template <class T> T sign(const T &a) {
return a == 0 ? 0 : (a < 0 ? -1 : 1);
}
template <class T> T floor(const T &a, const T &b) {
T A = abs(a), B = abs(b);
assert(B != 0);
return sign(a) * sign(b) > 0 ? A / B : -(A + B - 1) / B;
}
template <class T> T ceil(const T &a, const T &b) {
T A = abs(a), B = abs(b);
assert(b != 0);
return sign(a) * sign(b) > 0 ? (A + B - 1) / B : -A / B;
}
整数型数据读入速度研究(不确保准确度)
提示:个人研究,不确保准确度,请酌情相信。测试所用数据量为 \(10^7\) 。
| 方法 | 耗时(ms) | 浮动范围(ms) |
|---|---|---|
| 标准快读 | 800 | |
| 开启优化的 \(\tt{}cin\) | 1747.65 | 1622 - 1954 |
| \(\tt{}scanf\) | 4300 | |
| 朴素的 \(\tt{}cin\) | 6100 | |
| 不使用 \(\tt{}std\) 头文件的 \(\tt{}std::cin\) | 1685.89 | 1473 - 1878 |
隐式转换之:\(\tt sqrt\) 乘以 \(\tt sqrt\) 的转换问题
在使用 \(\tt{}sqrt\) 判断一个数字是否能被开平方时,一定要进行强制转换,否则会被当作浮点数进行计算。在某年的XCPC正式赛上本队因为这个问题多调了20分钟……
int num = 0;
for (int i = 1; i <= 100; ++ i) {
// if (sqrt(i) * sqrt(i) == i) ++ num; // 错误写法
if ((int)sqrt(i) * (int)sqrt(i) == i) ++ num; // 正确写法
}
cout << num;
随机数生成器 mt19937
位于 \(\tt random\) 这个库中,相较于传统的 \(rand()\) 函数,其可以高效的生成随机数。范围如下:
mt19937用于生成 \(\tt unsigned\ int\) 型数据;
mt19937_64用于生成 \(\tt unsigned\ long\ long\) 型数据。
一般用两种方式给定种子,分别是 time(0) 和 chrono::steady_clock::now().time_since_epoch().count() (需要引入 \(\tt chrono\) 这个库),其中后者获取的时间比前者更精确。
为了方便使用,我将这个函数进行了封装,使得可以直接输出值在 \([a, b]\) (边界可取)范围内的随机数,如下:
namespace Random { // 随机数生成器
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
int r(int a, int b) { return rnd() % (b - a + 1) + a; }
} // namespace Random
using namespace Random;
map 的使用技巧
下标查询与检查key值
| 采取方法 | 平均耗时(ms) |
|---|---|
map<LL, int> 检查key后查询 |
1366.67 |
map<LL, int> 直接查询 |
2576.07 |
map<pair<LL, LL>, int> 检查key后查询 |
2035.73 |
map<pair<LL, LL>, int> 直接查询 |
3343.33 |
结论:当不确定某次查询是否存在于容器中时,不要直接使用下标查询,而是先使用 count() 或者 find() 方法检查key值。
原因在于,一旦 map 中的一个元素被使用 [] 访问,无论此前是否被赋值,它都被视为已经存在。例如:使用 if(M["abc"]); 查询元素是否存在,则会被自动生成一个二元组 ("abc",zero) ,此时再使用 cout<<M.count("abc"); 答案是存在。
时间一长,就会出现非常多“零值二元组”,白白占用了空间,而由于 map 的复杂度为 \(\mathcal O(log S)\) ,这里的 \(S\) 为 map 的二元组数量,所以多出来的“零值二元组”会使得下一次查找的复杂度更高。
//不要这样写
int p = mp[i];
//这样写是好的
int q = 0;
if (mp.count(i)) q = mp[i];
测试如下
Round1:
构造一个 map<long long, int> ,生成 \(S=10^6\) 个随机数并加入容器,先检查key值再进行 \(N=10^6\) 次查询,重复15轮,统计查询花费的时间。理论时间复杂度 \(\mathcal O (N*logS) \approx 2*10^6\) 。
平均耗时为:1366.67 ms,时间浮动区间为:[1317, 1451] ms,符合预期。
代码如下:
#include <bits/stdc++.h>
using namespace std;
mt19937 rnd(time(0));
#define LL long long
const int Case = 15;
map<LL, int> mp;
void Ready() {
for (int i = 1; i <= 1000000; ++ i) {
LL x = rnd();
mp[x] = 1;
}
}
void Solve() {
int num = 0;
for (int i = 1; i <= 1000000; ++ i) {
LL x = rnd();
if (mp.count(x) != 0) {
if (mp[x] = 1) ++ num;
}
}
}
int main() {
freopen("Test.txt", "w", stdout);
Ready();
int T = Case;
double TIME = 0, Tmin = 0x3f3f3f3f, Tmax = 0;
while (T -- > 0) {
cout << "==============\n";
cout << "第" << Case - T << "轮测试:";
double start = clock();
Solve();
double end = clock();
cout << "用时" << end - start << "ms\n";
TIME += end - start;
Tmin = min(Tmin, end - start);
Tmax = max(Tmax, end - start);
}
cout << "\n\n==============\n\n";
cout << "平均耗时为:" << TIME / Case << " ms\n";
cout << "时间浮动区间为:[" << Tmin << ", " << Tmax << "] ms";
return 0;
}
Round2:
同上,不检查key值直接进行 \(N=10^6\) 次查询,重复15轮,统计查询花费的时间。由于查询最坏会额外产生 \(S\) 个空二元组,所以理论时间 \(\mathcal O (N*log(2S)) \approx 2*10^6\)。
平均耗时为:2576.07 ms,时间浮动区间为:[2188, 2885] ms,符合预期。
代码如下:
void Solve() {
int num = 0;
for (int i = 1; i <= 1000000; ++ i) {
LL x = rnd();
if (mp[x] = 1) ++ num;
}
}
Round3:
构造一个 map<pair<LL, LL>, int> ,生成 \(S=10^6\) 个随机数并加入容器,先检查key值再进行 \(N=10^6\) 次查询,重复15轮,统计查询花费的时间。理论时间复杂度 \(\mathcal O (N*logS) \approx 2*10^6\) 。
平均耗时为:2035.73 ms,时间浮动区间为:[1966, 2119] ms。注意到与预期相比慢了两倍左右,推测应该与 pair 相关。
Round4:
同上,不检查key值直接进行 \(N=10^6\) 次查询,重复15轮,统计查询花费的时间。
平均耗时为:3343.33 ms,时间浮动区间为:[2809, 3644] ms。
内置容器与自建结构体
事情起源来自于2022.07.25的牛客多校3,有一道打卡的最短路题一直超时卡不过去,在我的代码中使用了 map<pair<int, int>, int> 这样的构建方法,在进行上方的测试时我使用了自建结构体替代 pair ,结果意外的发现自建结构体的速度非常快。
| 采取方法 | 平均耗时(ms) |
|---|---|
map<LL, int> |
1366.67 |
map<pair<LL, LL>, int> |
2035.73 |
二参数结构体fff,map<fff, int> |
1485.33 |
map<tuple<LL, LL, LL>, int> |
3194.67 |
三参数结构体fff,map<fff, int> |
1446.27 |
结论:不要使用 pair 或者 tuple 容器构建 map ,而是使用自建结构体。
测试如下
Round3:构造一个 map<pair<LL, LL>, int> ,生成 \(S=10^6\) 个随机数并加入容器,先检查key值再进行 \(N=10^6\) 次查询,重复15轮,统计查询花费的时间。平均耗时为:2035.73 ms,时间浮动区间为:[1966, 2119] ms。
Round5:使用自建结构体代替Round3中的 pair ,平均耗时为:1485.33 ms,时间浮动区间为:[1434, 1555] ms。
代码如下:
const int Case = 15;
struct fff {
LL x, y;
friend bool operator < (const fff &a, const fff &b) {
if (a.x != b.x) return a.x < b.x;
return a.y < b.y;
}
};
map<fff, int> mp;
void Ready() {
for (int i = 1; i <= 1000000; ++ i) {
LL x = rnd(), y = rnd();
mp[{x, y}] = 1;
}
}
void Solve() {
int num = 0;
for (int i = 1; i <= 1000000; ++ i) {
LL x = rnd(), y = rnd();
if (mp.count({x, y}) != 0) {
if (mp[{x, y}] = 1) ++ num;
}
}
}
Round6:构造一个 map<tuple<LL, LL, LL>, int> ,平均耗时为:3194.67 ms,时间浮动区间为:[3070, 3377] ms。
Round7:使用自建结构体代替Round6中的 tuple ,平均耗时为:1446.27 ms,时间浮动区间为:[1394, 1516] ms。
RoundEX:自建一个六参数结构体构建 map ,平均耗时为:1504.73 ms,时间浮动区间为:[1464, 1568] ms。
map 与 unordered_map 的选取
事情的缘起是许久之前打 Codeforces 时,机缘巧合下发现有个红名大佬爆掉了(下图),顺藤摸瓜发现原因是在于这一场比赛出题人使用了
极其险恶的数据将所有基于哈希的数据结构全部杀死了(例如 \(\tt unordered\) 系列)。
赛后有人在评论区分享了出题人这一数据卡哈希的原理,原连接。简单来说就是编译器哈希自带了一些质数倍数,只要给的数据和这些自带的数据冲突,就会让哈希的复杂度从原来的平均 \(\mathcal O(1)\) ,最坏 \(\mathcal O(N)\) 下降到最坏 \(\mathcal O(N^2)\) 。
线上比赛有一定的概率会卡哈希,正式比赛一般不会这么干,所以赛时可以放心使用。
手写哈希函数
在使用基于哈希的容器(例如 unordered 系列)时,如果将不支持哈希的类型作为 key 值代入,编译器就无法正常运行,这时需要我们为其手写哈希函数。而我们写的这个哈希函数的正确性其实并不是特别重要(但是不可以没有),当发生冲突时编译器会调用 key 的 operator == 函数进行进一步判断。
本部分内容参考自:用struct做unordered_map的key。
对 pair 、tuple 定义哈希
struct hash_pair {
template <class T1, class T2>
size_t operator()(const pair<T1, T2> &p) const {
return hash<T1>()(p.fi) ^ hash<T2>()(p.se);
}
};
unordered_set<pair<int, int>, int, hash_pair> S;
unordered_map<tuple<int, int, int>, int, hash_pair> M;
对结构体定义哈希
需要两个条件,一个是在结构体中重载等于号(区别于非哈希容器需要重载小于号,如上所述,当冲突时编译器需要根据重载的等于号判断),第二是写一个哈希函数。注意 hash<>() 的尖括号中的类型匹配。
struct fff {
string x, y;
int z;
friend bool operator == (const fff &a, const fff &b) {
return a.x == b.x || a.y == b.y || a.z == b.z;
}
};
struct hash_fff {
size_t operator()(const fff &p) const {
return hash<string>()(p.x) ^ hash<string>()(p.y) ^ hash<int>()(p.z);
}
};
unordered_map<fff, int, hash_fff> mp;
对 vector 定义哈希
以下两个方法均可。注意 hash<>() 的尖括号中的类型匹配。
struct hash_vector {
size_t operator()(const vector<int> &p) const {
size_t seed = 0;
for (auto it : p) {
seed ^= hash<int>()(it);
}
return seed;
}
};
unordered_map<vector<int>, int, hash_vector> mp;
namespace std {
template<> struct hash<vector<int>> {
size_t operator()(const vector<int> &p) const {
size_t seed = 0;
for (int i : p) {
seed ^= hash<int>()(i) + 0x9e3779b9 + (seed << 6) + (seed >> 2);
}
return seed;
}
};
}
unordered_set<vector<int> > S;
考试平台相关
牛客
牛客平台 C++ 编译器1秒钟可以跑完 \(4 * 10^9\) (下图为某次多校时卡编译器的过法,给定范围是 \(N=2*10^6,S=2*10^7\) ,暴力做法用快排—— \(SlogN\) 的复杂度能够卡过本题,但要求常数极小)。
注:在C++11之前的版本,
sort的复杂度平均是 \(\mathcal O(NlogN)\) ,而在C++11之后,sort的复杂度最坏是 \(\mathcal O(NlogN)\) 。

暴力卡评测姬
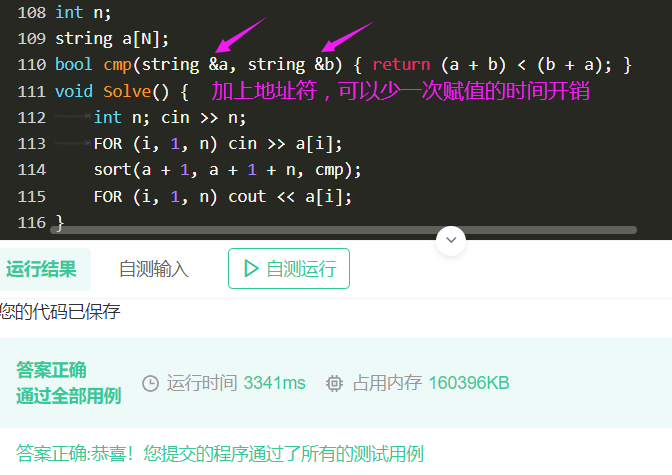
不够优秀,卡不了评测姬
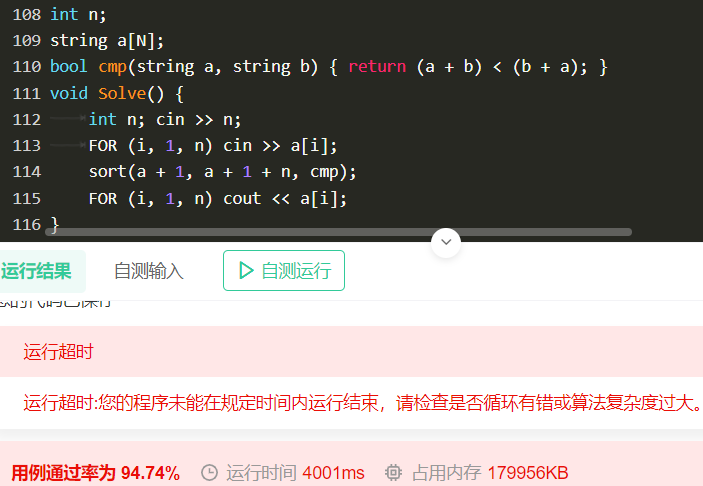
结论:一般情况log卡不掉,反而读入会卡常。——来自Bruce大佬
杭电
【截至2022.08.26】HDUOJ的C++版本还是C++11,这会导致很多语法用不了,而且运行速度极慢,一般本地运行时间乘4得到杭电运行时间。
以下是一些注意事项:
超时相关(按照严重性从高到低)
不要尝试使用哈希系列,而是尝试使用普通数组代替(例如
unordered开头的数据结构:例如在计算 \(SG\) 函数的mex值时,使用普通数组替代unordered_set),前者时间比后者慢10倍以上(由于超时,具体倍数不明);
vetcor建图比链式前向星慢大约10倍,需要谨慎使用;
需要输出
double型时,cout << fixed比printf慢大约5倍;
使用
namespace封装比不封装的情况慢大约2到5倍,需要谨慎使用;
使用带加速的
cin读入依旧比scanf慢2倍以上(超时,具体几倍不明),建议全部使用scanf;
重载符号时,建议写在外面,比写在结构体中快2倍;
错误相关
有时杭电需要读入到输入结尾的
EOF后停止,cin自带这个判断,即使用while (cin >> n)无需再判断是否读入到EOF了,但是scanf并不带这样的判断,需要人为写上去:while (scanf("%d", &n) != EOF);
杭电的
long double精度不如double,建议全部使用double;
一些结论
结论:HDUOJ的测试样例只有一组,且时间限制是根据std的时间来开的,所以很有可能会被卡时限,需要大力优化。——来自蒋老师
结论:玩杭电要小心 \(\tt{}cin\) 诈骗,可能需要上 \(\tt{}fread\) 快读。——来自群佬
结论:玩杭电需要学一大堆Useless的优化。——来自徐陆军、Kelin、懵哥
北大
POJ,不行。纯练思维还是可以的,就是编译器限制有亿点点多……
一些杂乱的知识点
- 使用
getchar的快读比开了加速的cin慢,不要使用。(——By Heltion)
何老师反复强调
(他真的,我哭死)
-
热知识:\(10^6*8=128MB\) 。
-
1<<n:左移运算的妙用,相当于计算 \(2^n\)。 -
n>>1:右移计算,相当于整除 \(2\),数学上表示为 \(\left \lfloor \frac{n}{2.0} \right \rfloor\)。 -
n&1:取出 \(n\) 在二进制表示下的最低位。 -
\(unsigned\ long\ long\) 的自然溢出等价于对 \(2^{64}\) 取模。
关于浮点数
声明
- 某些函数并不支持浮点数传入,例如
minmax函数,翻阅库之后我们可以发现,其只支持传入整数/字符串列表; - 某些函数对于浮点数的处理结果可能与我们设想的不同,例如
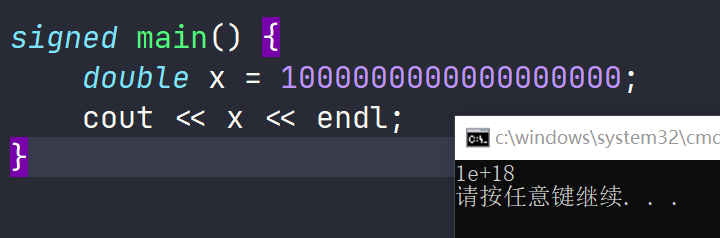
numeric_limits::min()函数,当我们使用numeric_limits<double>::min()或numeric_limits<long double>::min()时会得到0.0;而当我们使用numeric_limits<double>::max()时则会得到一个长度为 \(309\) 位的数字。 - 如果使用到了浮点数,一定要手动控制小数点后数字的数量(最好是直接写在头文件里以防万一),因为默认的长整型浮点数输出是科学计数法。

误差
老生常谈的问题,在打2022多校期间群友提出了几个很有意思的现象,在这里罗列一下。
pow开根号问题
在输出位数超过精度限制后,我们发现即便理论上应该输出整数的结果,但是有时候 pow 计算出来的答案并不是一个整数。
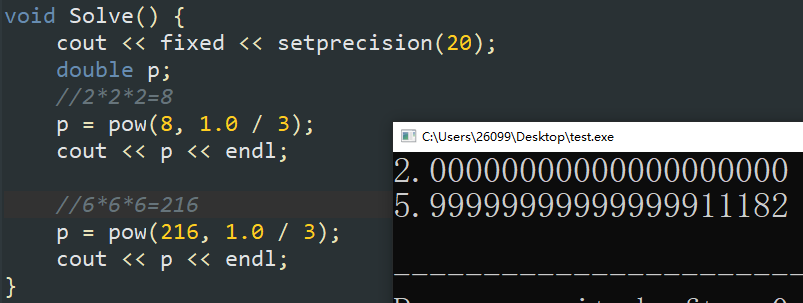
这一现象导致的直接结果就是我们无法利用隐式转换得到开根号之后的值(如下图,\(\sqrt[3]{216}\) 的答案应该是 \(6\) ,但是由于 pow 得到的是 \(5\) 开头的小数,隐式转换将小数部分全部舍去,就得到了十分错误的答案)。
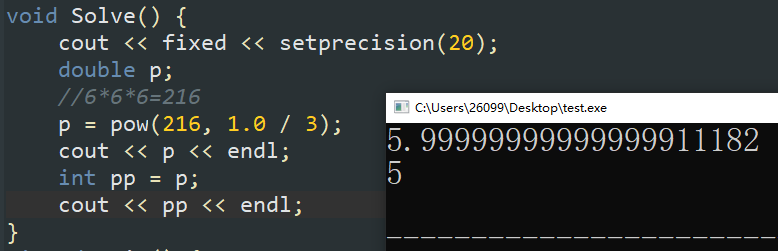
注:如果需要开立方根,C++库中自带函数
cbrt,用法与sqrt一致,且两者都保证精确。以后就不要乱用pow这种玄学东西了。
- 浮点数减法问题
如图:
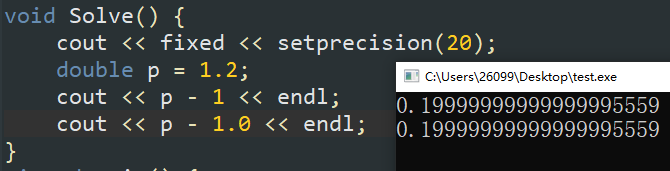
无符号整型负数溢出问题
\(\tt C++\) 的 \(\tt STL\) 库中查询容器的大小会返回你一个 \(\tt size\_t\) 类型的值,这个类型是无符号整型,这就意味着其不能为负数,如果将其减至负数,则会返回你一个随机数(下溢出之类的,没深入研究过)。
结论:在需要使用容器大小进行计算前请先将其转换为有符号整型,以免造成灾难。
for (int i = 0; i < (int)a.size() - 2; ++ i) {
cout << a[i] << endl;
}
有什么用呢,这里指路2021年ICPC沈阳E,在本场出题人@曾耀辉的知乎回答中也着重提到了这一点,要时刻警惕。
Stack的本质与其弊端(MLE问题)
本部分来源于:2023牛客暑期多校训练营8 - H 。
在C语言中,stack 默认是使用 deque 实现的,而 deque 有一个特点在于其初始空间极大,所以开的数量一多就会导致MLE。建议在需要使用 stack 的地方直接换用 vector 。

可变模版参数 template <class... Args>
我们可以使用这个模板参数非常方便的输出任意类型、任意数量的变量,我将其用在我的 \(\tt Debug\) 函数里面,方便自己检查错误:
template <class... Args> void _(Args... args) { // 可变模板输出
auto _ = [&](auto x) -> void { cout << x << " "; };
cout << "--->";
int arr[] = {(_(args), 0)...};
cout << "\n";
}
一些Debug程序
本部分参考自 。
我们可以新建一个头文件 <wida.h> ,随后将debug的内容放到这个头文件中去,这样可以减少程序中不需要的代码。
很显然,我们发现上方的模板参数不能够直接输出顺序容器、pair 等内容,这在比赛需要debug时依旧非常难受,所以,我们需要用一些技巧,以下是我的完整debug程序:
template <class T, class = decay_t<decltype(*begin(declval<T>()))>,
class = enable_if_t<!is_same<T, string>::value>>
ostream &operator<<(ostream &os, const T &c) { // 定义容器的流输出
for (auto it = c.begin(); it != c.end(); ++it) {
os << &", "[2 * (it == c.begin())] << *it;
}
return os;
}
template <class T1, class T2>
ostream &operator<<(ostream &os, const pair<T1, T2> &p) { // 定义pair的流输出
return os << '[' << p.first << ", " << p.second << ']';
}
template <class... Args> void _(Args... args) { // 可变模板输出
auto _ = [&](auto x) -> void { cout << x << " "; };
cout << "--->";
int arr[] = {(_(args), 0)...};
cout << "\n";
}
template <class T, class = decay_t<decltype(*begin(declval<T>()))>,
class = enable_if_t<!is_same<T, string>::value>>
void _(T args) { cout << "{" << args << "}\n"; } // 容器输出
template <class T> void _i(T args) { // 旧时代容器输出
cout << "{";
for (auto i : args) cout << i << ", ";
cout << "}\n";
}
template <class T> void _ii(T args) { // 旧时代容器输出
cout << "{";
for (auto [i, j] : args) cout << i << " " << j << ", ";
cout << "}\n";
}
这里再分享一个别人的debug程序:
template <class T1, class T2>
ostream &operator<<(ostream &os, const pair<T1, T2> &p) {
return os << '{' << p.first << ", " << p.second << '}';
}
template <class T, class = decay_t<decltype(*begin(declval<T>()))>,
class = enable_if_t<!is_same<T, string>::value>>
ostream &operator<<(ostream &os, const T &c) {
os << '[';
for (auto it = c.begin(); it != c.end(); ++it)
os << &", "[2 * (it == c.begin())] << *it;
return os << ']';
}
//support up to 5 args
#define _NTH_ARG(_1, _2, _3, _4, _5, _6, N, ...) N
#define _FE_0(_CALL, ...)
#define _FE_1(_CALL, x) _CALL(x)
#define _FE_2(_CALL, x, ...) _CALL(x) _FE_1(_CALL, __VA_ARGS__)
#define _FE_3(_CALL, x, ...) _CALL(x) _FE_2(_CALL, __VA_ARGS__)
#define _FE_4(_CALL, x, ...) _CALL(x) _FE_3(_CALL, __VA_ARGS__)
#define _FE_5(_CALL, x, ...) _CALL(x) _FE_4(_CALL, __VA_ARGS__)
#define FOR_EACH_MACRO(MACRO, ...) \
_NTH_ARG(dummy, ##__VA_ARGS__, _FE_5, _FE_4, _FE_3, _FE_2, _FE_1, _FE_0) \
(MACRO, ##__VA_ARGS__)
//Change output format here
#define out(x) #x " = " << x << "; "
#define _(...) cerr << FOR_EACH_MACRO(out, __VA_ARGS__) << "\n"
随后在主代码中加入以下内容:
#ifndef ONLINE_JUDGE
// #define cerr cout // 如果需要直接输出,则取消本行注释
#include <bits/wida.h>
#else
#define _(...)
#endif
测试编译器版本
\(\tt C++20\)
\(\tt map\) 在 \(\tt C++20\) 中新增了 contains 函数,可以用于测试,如下:
#include <bits/stdc++.h>
using namespace std;
int main() {
map<string, int> mp;
mp["abcde"] = 2;
cout << mp.contains("abcde");
return 0;
}
不常用但是有必要知道的 \(\tt Markdown\) 语法
时间复杂度
使用
\mathcal输出 \(\mathcal O\) 。
部分常见符号的Markdown专属语法
有时Markdown转换为HTML语言,部分语法会出现错误,我们使用专属语法来规避——
- 大于小于号的Markdown专属语法为
\lt和\gt: \(\lt\) 、 \(\gt\) 。- 和符号(&)的专属语法尚未找到。
公式居中
使用两个
$符号可以使得公式居中,例如——\[dp[n][m]= \left\{\begin{matrix} dp[n-m][m] & n\ge m \\ 0 & n \lt m \\ \end{matrix}\right.\]
指定大小的括号
从大括号到小括号的语法依次为
\Bigg\bigg\Big\big,其中,左括号在末尾加l,右括号为r。例如——\[\Biggl(\biggl(\Bigl(\bigl((x)\bigr)\Bigr)\biggr)\Biggr) \]
乱七八糟的
\(\iff\) :
\iff
\(\equiv\) :
\equiv











 浙公网安备 33010602011771号
浙公网安备 33010602011771号