2018 浙江省赛(TeamVP)
比赛相关信息
比赛信息
比赛名称: The 15th Zhejiang Provincial Collegiate Programming Contest
比赛地址: Vjudge全部参赛队伍: 280 + 5*
金: 9题,1000m
银: 7题,582m
铜: 6题,363m
比赛过程回顾
| A | B | C | D | E | F | G | H | I | J | K | L | M | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 提交次数 | 1 | 1 | 1 | 5 | 1 | 1 | |||||||
| 首次提交时间 | 0:15:15 | 0:18:49 | 0:56:17 | 2:59:21 | 0:32:25 | 0:11:07 | |||||||
| 首A时间 | 0:15:15 | 0:18:49 | 0:56:17 | 0:32:25 | 0:11:17 | ||||||||
| 状态 | ✔ | ✔ | 补 | ✔ | ⚪补 | ✔ | ✔ | ||||||
| 知识点 | 组合数学 / 概率 | DP | 图论 / 差分约束 / 贪心 | 数论 / 二分 | 数学规律 | 模拟 |
✔:比赛时通过;⚪:比赛时尝试过;补:已补题。
部分题解与小结
A - Peak
小评
\(\mathcal{Consider\ by\ Hwh\ \&\ Wcj}\)
\(\mathcal{Solved\ by\ Wida}\)
打卡题(1 / 5),队友在跟我说题意的时候听错了,直到第一遍码完后发现过不了样例才意识到理解错题意,于是决定先把更简单的 \(\tt{}M\) 做了再重构代码,导致时间上略慢。
题意
给出长度为 \(N\) 的序列,询问其是否为凸序列。
思路
赛时思路
先找到序列最大值,再分别向左右遍历。
AC代码
点击查看代码
//====================
#define int LL
const int N = 1e6 + 7;
int a[N];
//====================
void Solve() {
int n; cin >> n;
for (int i = 1; i <= n; ++ i) cin >> a[i];
int m = max_element(a + 1, a + 1 + n) - a;
int flag = 0;
for (int i = m - 1; i >= 1; -- i)
if (a[i - 1] >= a[i])
flag = 1;
for (int i = m + 1; i <= n; ++ i)
if (a[i - 1] <= a[i])
flag = 1;
if (flag == 1 || m == 1 || m == n) cout << "No" << endl;
else cout << "Yes" << endl;
}
B - King of Karaoke
小评
\(\mathcal{Consider\ by\ Wcj}\)
\(\mathcal{Solved\ by\ Wida}\)
打卡题(2 / 5),倒数第二简单,不解释。
题意
思路
AC代码
点击查看代码
const int N = 1e5 + 7;
int a[N], b[N];
void solve() {
int n; cin >> n;
map<int, int> mp; int m = 0;
for (int i = 1; i <= n; ++ i) cin >> a[i];
for (int i = 1; i <= n; ++ i) cin >> b[i];
for (int i = 1; i <= n; ++ i) mp[a[i] - b[i]] ++ ;
for (auto [i, j] : mp) m = max(m, j);
cout << m << endl;
}
C - Magic 12 Months
https://blog.csdn.net/V5ZSQ/article/details/80205105
I - Magic Points
\(\mathcal{Solved\ by\ Wida(After)}\)
小评
这是一道和 \(\tt{}K\) 一样处境的题目,但比 \(\tt{}K\) 题惨多了。在比赛全程几乎都无人问津这道题,于是我也就象征性的看了一下题目的意思,以为需要涉及到斜率等复杂计算,于是便没有细想。
赛后复盘的时候发现这居然也是一道规律+模拟的打卡题(?),只要想到了几乎是秒做的程度,代码量也非常小。
题意
在二维坐标轴上有 \(4*N-4\) 个不同的点,排布如下图。
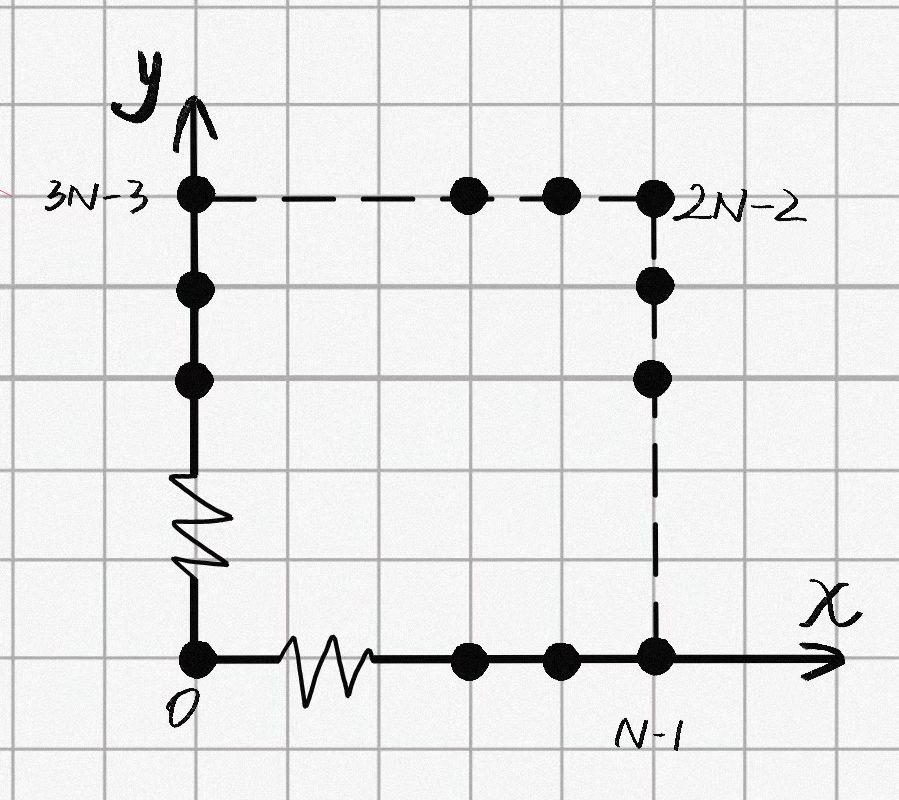
众所周知,两点确定一条直线。现在你需要连出 \(N\) 根不平行于坐标轴的直线,使得这些直线相交点的数量最多,输出任意一种方案即可。可以证明至少存在一种方案。
思路
贪心可得,要使得直线相交点的数量最多,那么每一条直线与别的直线相交的点的数量都应当最多,即:后画上去的直线应与所有已有的直线相交。相交点的数量最大值即为 \(\sum_{i=1}^{n-1} i\) 。容易得到 \(N-1\) 条直线的构造方式,如下。
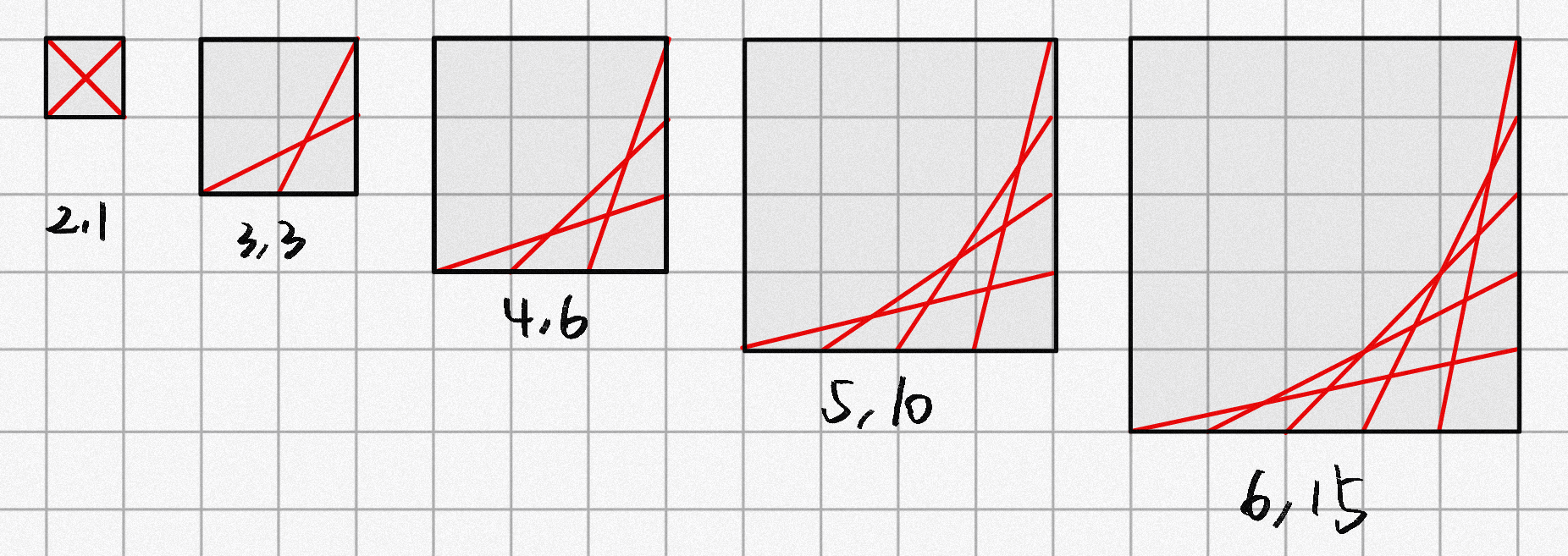
现在的问题是,能否将剩下的一条直线放入图中,使得其与已有的 \(N-1\) 条直线交 \(N-1\) 个点。从数学方法上论证,只需要这条直线的斜率的绝对值与此前所有直线斜率的绝对值均不相等即可。此前的直线斜率为 \(\frac{1}{N-1},\frac{2}{N-2},\frac{3}{N-3},…,\frac{N-1}{1}\) ,只要找到一个 \(X\) ,使得 \(X \neq i\) 并且 \(gcd(X,N-i)=1\) 即可。幸运的是,恒存在这样的直线:斜率为 \(\frac{N-2}{1}\) ,\(\frac{1}{N-2}\) , \(\frac{N-2}{N-1}\)或 \(\frac{N-1}{N-2}\) ,但是需要特判 \(N = 2\) 的情况。
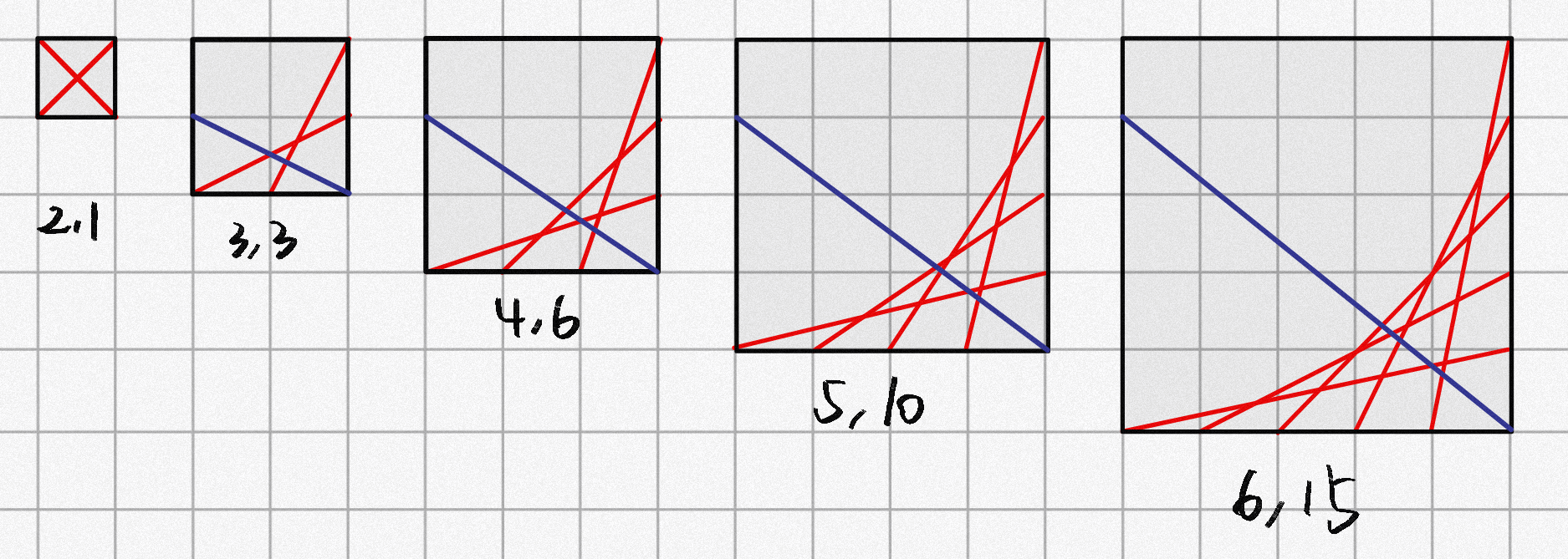
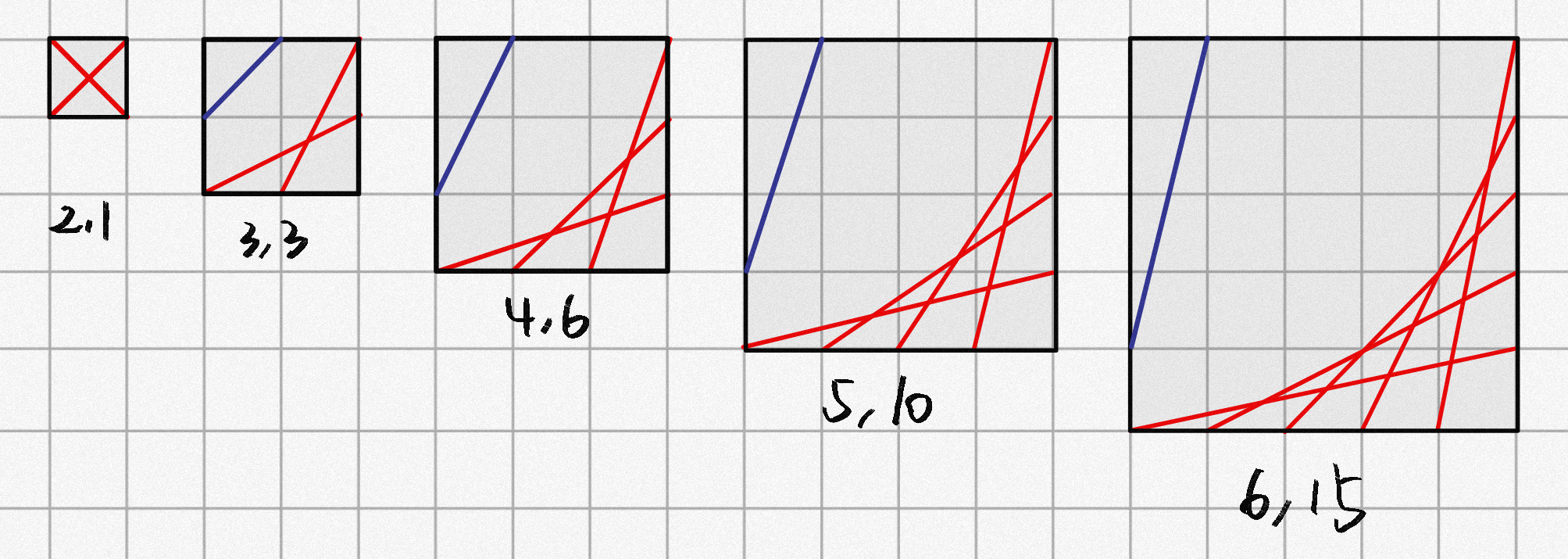
AC代码
点击查看代码
void Solve() {
int n; cin >> n;
if (n == 2) {
cout << "0 2 1 3" << endl;
return;
}
for (int i = 0; i < n - 1; ++ i) cout << i << " " << n + i << " ";
cout << n - 1 << " " << 3 * (n - 1) + 1 << endl;
// cout << 3 * n - 4 << " " << 4 * n - 5 << endl;
}
J - CONTINUE...?
\(\mathcal{Consider\ by\ Hwh\ \&\ Wcj}\)
\(\mathcal{Solved\ by\ Hwh}\)
小评
打卡题(3 / 5),初见两个队友想了有一会儿,我了解题意之后感觉不是自己擅长的,就交给两个队友了。没过一会儿队友讨论完了,码完直接一发过,非常顺滑(Jls:还是队友牛逼呀)。
题意
\(N\) 个学生从 \(1\) 到 \(N\) 编号,每个人都带有等同自己编号数量的宝石,要求将学生分成 \(G_1,G_2,G_3,G_4\) 四组,规定:
- 每位学生都要被分到一个组;
- 女生只能被分到 \(G_1,G_2\) 组,男生同理;
- 要求 \(G_1,G_3\) 组的宝石数量等于 \(G_2,G_4\) 组的宝石数量。
输出任意一种情况,不然则输出 \(-1\) 。
思路
赛时思路(数论 + 暴力)
将整数 \(1\) 到 \(N\) 分成两组的情况为: \(\sum_{i=1}^n i \mid 2\) 。
本题的难点在于要将学生分为四组,而分析后我们可以发现,首先我们可以先不考虑四组的情形,只考虑将所有人分成两组,使得两组的宝石数相等,再去区分男女即可。
而分成两组的方式也可以非常暴力,在保证能够分成两组的情况下,只需要倒序遍历数组即可。
AC代码
点击查看代码
//====================
const int N = 1e6 + 7;
int a[N], v[N];
//====================
void Solve() {
int n; cin >> n;
for (int i = 1; i <= n; ++ i) {
v[i] = 0;
char x; cin >> x;
a[i] = x - '0';
}
int add = (1 + n) * n / 2, num = 0;
if (add % 2 == 1) {
cout << "-1" << endl;
return;
}
for (int i = n; i >= 1; -- i) {
if (num + i <= add / 2) {
num += i;
v[i] = 1;
}
}
for (int i = 1; i <= n; ++ i) {
if (a[i] % 2 == 0) cout << 1 + v[i];
else if (a[i] % 2 == 1) cout << 3 + v[i];
}
cout << endl;
}
K - Mahjong Sorting
\(\mathcal{Consider\ by\ Hwh\ \&\ Wida}\)
\(\mathcal{Solved\ by\ Wida(After)}\)
小评
在比赛的前半段,因为榜单里做这道题的人极少,便迟迟没开这题,中途队友 \(\mathcal Hwh\) 也尝试解这道题,但是限于过长的题干以及较少的通过人数也没有细看。到比赛后半段时解这一题的人逐渐多了起来,才正式开了这道题。题干非常长,题意也不是特别清晰,连猜带蒙的理解完题意才意识到这是一道模拟大水题,应该是能切掉的,于是开始模拟。但是由于时间较晚,队员状态也不是特别好,在连WA五次后还是没能解出来。
赛后查阅题解,发现全网关于这道题的题解只有一篇,但在参考AC代码后发现这道题应该算是打卡题之一,可能是因为过长的题干导致大家都以为这道题难度极高,这一点需要反思。
题意
背景知识如下:
本题的麻将一共有 \(3*M+1\) 块,分别是 \(M\) 块条子, \(M\) 块竹, \(M\) 块点,这 \(3*M\) 块普通麻将上面都有一个数字代表它的大小,以及 \(1\) 块特殊的白龙。 \(3*M\) 块普通麻将按照一般顺序排序从前往后依次为:条子,竹,点。
现在,从 \(3*M\) 块普通麻将中选出一个“幸运块”,然后再从全部 \(3*M+1\) 块麻将中选出 \(N\) 块麻将进行排序。规定新的排序方式如下:
- 如果这 \(N\) 块麻将中有“幸运块”,那么需要放在最左边;
- 如果这 \(N\) 块麻将中有白龙,那么需要放在幸运块原来的位置。
给出按新排序方式排序过后的 \(N\) 块麻将的顺序,求解“幸运块”可能的数量。保证至少有一种解。
思路
弄懂题目之后很显然的想到了模拟。可以分成以下几种情况:
- 白龙在第一个时,答案与第二个有关;
- 白龙在最后一个时,答案与倒数第二个有关;
- 白龙在中间时,与前后两个都有关;
- 不存在白龙时,答案与 \(N\) 有关。
注意以上各情况均为理想情形,要加上一些判断:
- \(N\) 为 \(1\) 时,所有块都能为“幸运块”,直接输出 \(3*M\) ;
- 白龙在第二个时,第一个块也有可能是“幸运块”,答案加一;
- 第一个和第二个均不为白龙,且第一个大于第二个,说明第一个是被移动过来的“幸运块”,直接输出 \(1\) 。
各种情况的先后顺序要仔细考虑,答案极多,满足所有条件即可。
AC代码
点击查看代码
//====================
const int N = 1e6 + 7;
int num[N];
//====================
void Solve() {
int n, m, s = 0; cin >> n >> m;
for (int i = 1; i <= n; ++ i) {
char x; cin >> x;
int w = 0;
if (x != 'W') cin >> w;
if (x == 'C') num[i] = w;
else if (x == 'B') num[i] = m + w;
else if (x == 'D') num[i] = m + m + w;
else num[i] = 0, s = i;
}
int ans = 0;
if (n == 1) ans = 3 * m;
else if (num[1] > num[2] && s != 1 && s != 2) ans = 1;
else if (s == 0) ans = 3 * m - n + 1;
else if (s == 1) ans = num[2] - 1;
else {
if (s == 2) ans = 1;
if (s == n) ans += 3 * m - num[n - 1];
else ans += num[s + 1] - num[s - 1] - 1;
}
cout << ans << endl;
}
L - Doki Doki Literature Club
小评
\(\mathcal{Consider\ by\ Hwh}\)
\(\mathcal{Solved\ by\ Wida\ \&\ Wcj}\)
打卡题(4 / 5),刚看到这题的时候以为是字典树,就交给队友读了。这道题题目较长,但是读懂了之后发现就是一个自定义排序,写起来不难。
题意
给定 \(N\) 个单词及其权值,你需要按照规定顺序排序:
- 权值大的在前;
- 权值相同时,字典序小的在前。
要求选出前 \(M\) 个,输出总值( \(\sum_{i=1}^m (m - i + 1) * w_i\) ,其中 \(w_i\) 是第 \(i\) 个单词的权值)与连成的句子。
思路
自定义排序,暴力计算总值。
AC代码
点击查看代码
struct Node{
int x;
string y;
};
bool cmp(Node x, Node y) {
if (x.x == y.x) return x.y < y.y;
return x.x > y.x;
}
void solve() {
vector<Node> ver;
string ans;
int cnt = 0;
int n, m; cin >> n >> m;
for (int i = 1; i <= n; ++ i) {
string s; int num;
cin >> s >> num;
ver.push_back({num, s});
}
sort(ver.begin(), ver.end(), cmp);
for (int i = 0; i < m; ++ i) {
auto [x, y] = ver[i];
ans += " " + y;
cnt += (m - i) * x;
}
cout << cnt << ans << endl;
}
M - Lucky 7
小评
\(\mathcal{Consider\ by\ Wcj}\)
\(\mathcal{Solved\ by\ Wida}\)
打卡题(5 / 5),最简单的一题,不解释了。
题意
思路
AC代码
点击查看代码
const int N = 1e5 + 7;
int a[N];
void solve() {
int n, k; cin >> n >> k;
for (int i = 1; i <= n; ++ i) cin >> a[i];
for (int i = 1; i <= n; ++ i) {
if ((a[i] + k) % 7 == 0) {
cout << "Yes" << endl;
return;
}
}
cout << "No" << endl;
}
文 / WIDA
2022.03.31 成文
首发于WIDA个人博客,仅供学习讨论



 浙公网安备 33010602011771号
浙公网安备 33010602011771号